半挂汽车列车横向稳定性控制：基于TruckSim与Simulink联合仿真

半挂汽车列车4自由度6轴整车model，横向稳定性控制，在低附着系数路面，进行典型3个工况，角阶跃，双移线，方向盘转角。采用算法：模糊PID，制动力矩分配，最优滑移率滑膜控制。以上基于trucksim和simulink联合仿真，有对应 p-a-p-e-r参考

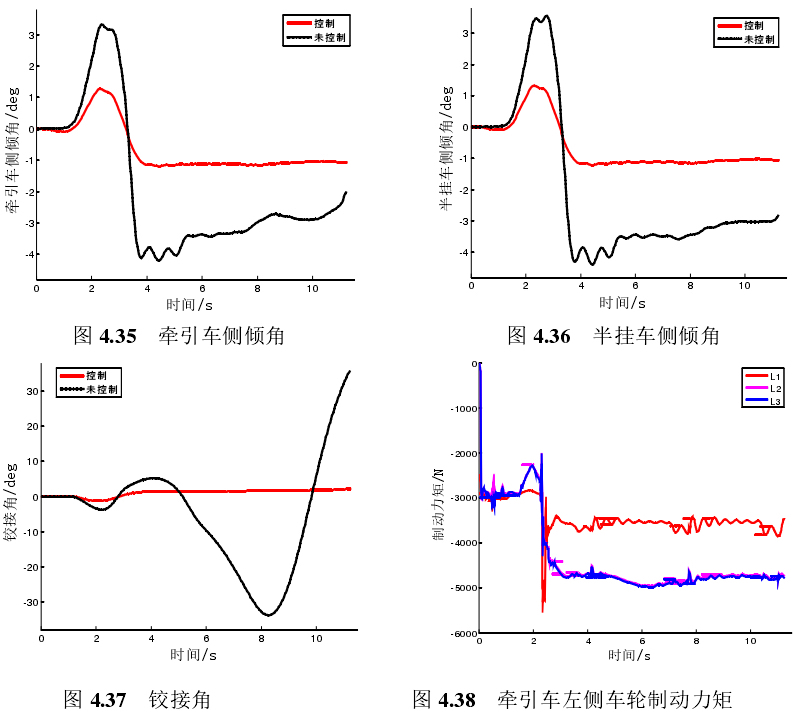
在汽车工程领域，半挂汽车列车的横向稳定性一直是研究热点。特别是在低附着系数路面，保障车辆行驶安全与稳定更是重中之重。今天咱就来聊聊基于4自由度6轴整车model的半挂汽车列车横向稳定性控制，以及在TruckSim和Simulink联合仿真环境下的实现。

工况设定：典型驾驶场景模拟

咱选了三个典型工况：角阶跃、双移线和方向盘转角。这三种工况基本覆盖了车辆在实际行驶中遇到的突发转向情况。比如说角阶跃工况，模拟的就是驾驶员突然转动方向盘，车辆迅速响应的过程。

算法应用：多管齐下保障稳定

模糊PID控制

模糊PID控制是个好东西，它能根据实际情况动态调整控制参数。传统的PID控制依赖精确的数学模型，但车辆行驶环境复杂多变，模糊PID就派上用场了。在Simulink里搭建模糊PID控制器，代码大概像这样：

matlab 复制代码

% 定义模糊推理系统
fis = newfis('fuzzy_pid');

% 添加输入变量
fis = addvar(fis,'input','e',[-3 3]);
fis = addmf(fis,'input',1,'NB','zmf',[-3 -1]);
fis = addmf(fis,'input',1,'NS','trimf',[-3 0 3]);
% 类似地添加其他隶属度函数

% 添加输出变量
fis = addvar(fis,'output','kp',[0 10]);
% 添加kp的隶属度函数

% 定义模糊规则
rulelist = [1 1 1 1 1;
            2 2 2 1 1;
            % 更多规则...
            ];
fis = addrule(fis,rulelist);

% 保存模糊推理系统
writefis(fis,'fuzzy_pid.fis');

这里，先创建了一个模糊推理系统，定义了输入变量（比如误差e）和输出变量（像kp），然后添加隶属度函数描述变量的模糊状态，最后通过规则列表确定如何根据输入得到输出。模糊PID能实时根据车辆状态调整控制参数，让控制更灵活。

制动力矩分配

制动力矩分配算法能合理分配各个车轮的制动力，以提高车辆稳定性。不同的工况和路面条件下，每个车轮所需的制动力不同。代码思路大概是这样：

matlab 复制代码

function [brake_torque] = distribute_brake_torque(vehicle_state, road_condition)
    % 根据车辆状态（速度、转向角等）和路面条件计算制动力矩分配
    if road_condition == 'low_friction'
        % 低附着系数路面的分配策略
        front_brake = vehicle_state.speed * 0.2;
        rear_brake = vehicle_state.speed * 0.3;
        % 更多车轮的分配计算...
    else
        % 其他路面的分配策略
    end
    brake_torque = [front_brake, rear_brake,...];
end

这个函数根据车辆当前状态和路面状况，为各个车轮分配制动力矩，确保车辆在不同情况下都能有效制动且保持稳定。

最优滑移率滑膜控制

最优滑移率滑膜控制能让车轮尽可能工作在最优滑移率附近，提高轮胎与地面的附着力。简单理解，滑膜控制就像给车轮状态设定一个"滑动轨迹"，让它沿着这个轨迹达到最优滑移率。

matlab 复制代码

% 滑膜控制相关代码
s = calculate_sliding_surface(vehicle_state);
% 根据滑膜面s计算控制输入
if s > 0
    control_input = max_control;
else
    control_input = min_control;
end

这里通过计算滑膜面s，根据s的值来确定控制输入，从而调整车轮的滑移率。

联合仿真：TruckSim与Simulink的强强联手

基于TruckSim和Simulink联合仿真，能充分利用两者优势。TruckSim提供高精度的车辆动力学模型，Simulink用于搭建控制算法。通过接口连接两者，就能进行完整的车辆控制仿真。

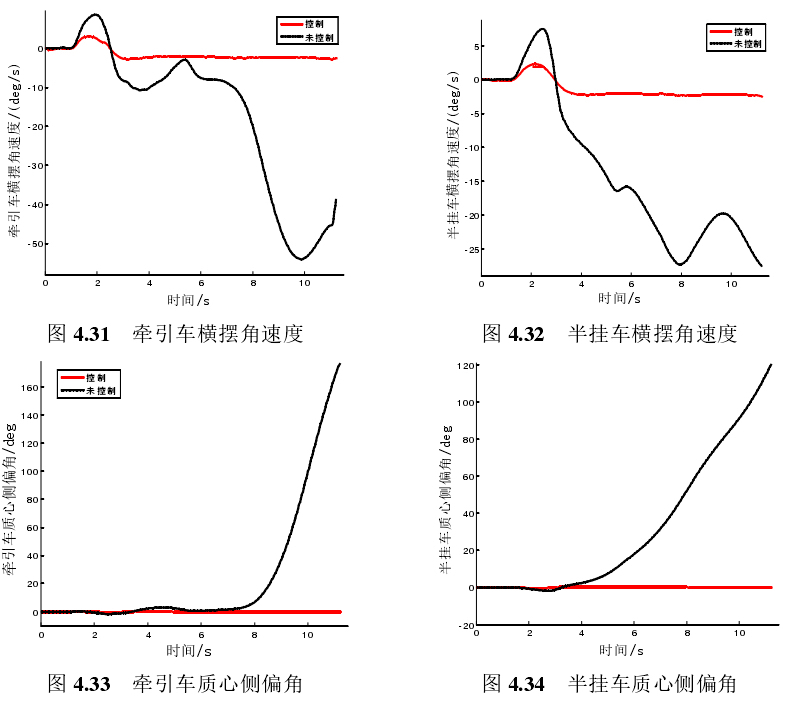
咱有相关paper参考，能深入研究每个细节。这种联合仿真的方式，让我们在研究半挂汽车列车横向稳定性控制上，能更直观、准确地看到不同算法在不同工况下的效果，为实际车辆控制系统开发提供有力支持。

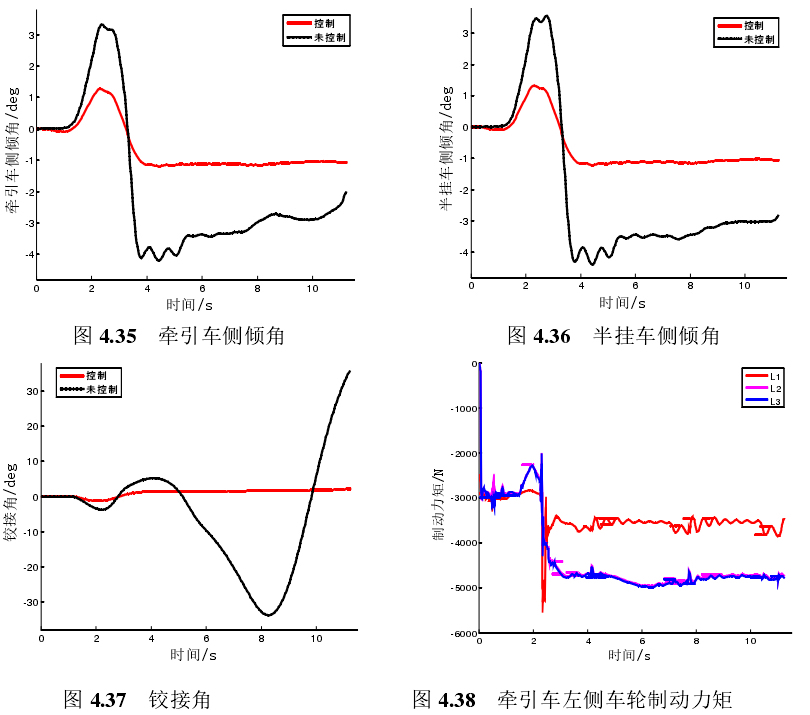
总的来说，通过这几种算法和联合仿真，能更好地保障半挂汽车列车在低附着系数路面的横向稳定性，为交通安全添砖加瓦。