数据结构 —— 并查集

并查集（Union-Find）是一种高效处理 动态连通性 问题的数据结构，主要用于解决 "元素分组" 和 "判断元素是否属于同一组" 的场景。它支持两种核心操作：合并（Union） 两个集合，以及查询（Find） 元素所属集合的根节点，进而判断元素是否连通。

一、并查集的核心概念

并查集是一种树型的数据结构，用于处理一些不相交集合的合并及查询问题（即所谓的并、查）。比如说，我们可以用并查集来判断一个森林中有几棵树、某个节点是否属于某棵树等。

集合（Set） ：由若干元素组成的群体，每个集合有一个唯一的根节点（Root） 作为标识。
父节点（Parent）：每个元素有一个指向其父节点的引用，根节点的父节点是自身。
核心操作：

- Find(x) ：查找元素x所在集合的根节点(这里以顶级元素相称)（路径上的元素会指向根节点，优化后续查询）。
- Union(x, y) ：将元素x和y所在的集合合并为一个集合（通过根节点关联）。
- **Init：**为每个元素创建独立集合，每个元素的父节点指向自己。
- isConnected(x,y)：判断元素 x 和 y 是否属于同一集合。

二、具体操作

1.Find()函数

实现：

首先我们需要定义一个数组：int pre[1000]; （数组长度依题意而定）。这个数组记录了每个人的上级是谁。这些人从0或1开始编号（依题意而定）。比如说pre[2]=1 就表示 2 号的上级是 1 号。如果一个人的上级就是他自己，那说明他就是上级，查找到此结束。

java 复制代码

int find(int x)					// 查找x的顶级元素
	while(pre[x] != x)			// 如果x的上级元素不等于x,说明还未找到
		x = pre[x];			    // 让x的上级元素继续找
	return x;					// 返回x的顶级元素
}

2.join()函数

实现：

join(x,y) 的执行逻辑如下：

寻找 x 的代表元（即顶级元素）；
寻找 y 的代表元（即顶级元素）；
如果 x 和 y 不相等，则随便选一个人作为另一个人的上级，如此一来就完成了 x 和 y 的合并。

java 复制代码

void join(int x,int y)                  
    int fx=find(x), fy=find(y);  // 求得x，y的顶级元素
    if(fx != fy)                 // 如果两者的顶级元素不同         
        pre[fx]=fy;              // 任选其中一个元素作为另一个元素的上级        
}

3.isConnected()函数

实现：

isConnected()函数是基于 find()函数来实现的，用于判读两个顶点的顶级元素(即根节点)是否相同。

java 复制代码

public boolean isConnected(int x, int y) {
        // 只需判断两者的根节点是否相同
        return find(x) == find(y);
    }

三、路径压缩算法

1.优化 find()函数

问题引入：

前面介绍的 join(x,y) 实际上为我们提供了一个将不同节点进行合并的方法。通常情况下，我们可以结合着循环来将给定的大量数据合并成为若干个更大的集合（即并查集）。但是问题也随之产生，我们来看这段代码：

java 复制代码

if(fx != fy)  
	pre[fx]=fy;

这里并没有明确谁是谁的前驱（上级）的规则，而是我直接指定后面的数据作为前面数据的前驱（上级）。那么这样就导致了最终的树状结构无法预计，即有可能是良好的 n 叉树，也有可能是单支树结构（一字长蛇形）。试想，如果最后真的形成单支树结构，那么它的效率就会及其低下（树的深度过深，那么查询过程就必然耗时）。

而最理想的情况就是所有节点的直接上级都是顶级元素(根节点)，这样整个树的结构就只有两级，此时查询顶级元素只需要一次。即路径压缩算法。

我们可以通过递归的方法来逐层修改返回时的某个节点的直接前驱（即pre[x]的值）。简单说来就是将x到根节点路径上的所有点的pre（上级）都设为根节点。下面给出具体的实现代码：

java 复制代码

int find(int x)     				// 查找结点 x 的根结点 
{
    if(pre[x] == x) return x;		// 递归出口：x 的上级为 x 本身，即 x 为根结点        
    return pre[x] = find(pre[x]);	// 此代码相当于先找到根结点 rootx，然后 pre[x]=rootx 
}

该算法存在一个缺陷：只有当查找了某个节点的顶级元素后，才能对该查找路径上的各节点进行路径压缩。换言之，第一次执行查找操作的时候是实现没有压缩效果的，只有在之后才有效。

2.加权标记法

主要思路：

加权标记法需要将树中所有节点都增设一个权值，用以表示该节点所在树中的高度（比如用rank[x]=3表示 x 节点所在树的高度为3）。这样一来，在合并操作的时候就能通过这个权值的大小来决定谁当谁的上级。

在合并操作的时候，假设需要合并的两个集合的顶级元素分别为 x 和 y，则只需要令pre[x] = y 或者pre[y] = x 即可。但我们为了使合并后的树不产生退化（即：使树中左右子树的深度差尽可能小），那么对于每一个元素 x ，增设一个rank[x]数组，用以表达子树 x 的高度。在合并时，如果rank[x] < rank[y]，则令pre[x] = y；否则令pre[y] = x。

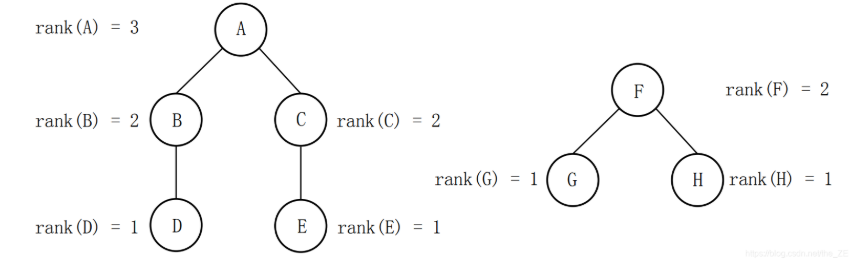
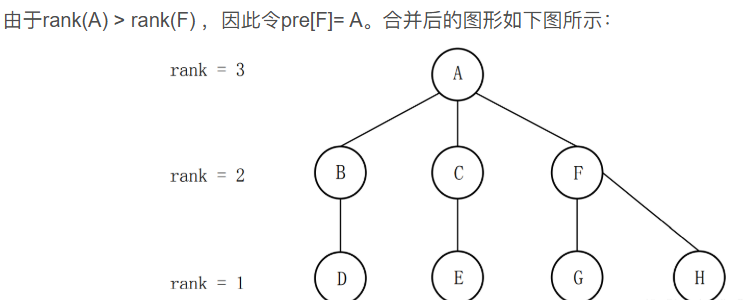
实现：

加权标记法的核心在于对rank数组的逻辑控制，其主要的情况有：

1、如果rank[x] < rank[y]，则令pre[x] = y；

2、如果rank[x] == rank[y]，则可任意指定上级；

3、如果rank[x] > rank[y]，则令pre[y] = x；

在实际写代码时，为了使代码尽可能简洁，我们可以将第 3 点单独作为一个逻辑选择，然后将 1、2 点作为另一个选择（反正第2点任意指定上级嘛），所以具体的代码如下：

java 复制代码

void union(int x,int y)
{
    x=find(x);							// 寻找 x 的代表元
    y=find(y);							// 寻找 y 的代表元
    if(x==y) return ;					// 如果 x和 y 的代表元一致，说明他们共属同一集合，则不需要合并，直接返回；否则，执行下面的逻辑
    if(rank[x]>rank[y]) pre[y]=x;		// 如果 x的高度大于 y，则令 y 的上级为 x
    else								// 否则
    {
        if(rank[x]==rank[y]) rank[y]++;	// 如果 x 的高度和 y 的高度相同，则令 y 的高度加1
        pre[x]=y;						// 让 x 的上级为 y
    }
}

四、总结

1、用集合中的某个元素来代表这个集合，则该元素称为此集合的代表元(根节点或顶级元素)；

2 、一个集合内的所有元素组织成以代表元为根的树形结构；

3 、对于每一个元素 x，pre[x] 存放 x 在树形结构中的父亲节点（如果x 是根节点，则令 pre[x] = x）；

4 、对于查找操作，假设需要确定 x 所在的集合，也就是确定集合的代表元。可以沿着 pre[x] 不断在树形结构中向上移动，直到到达根节点。

5、基于这样的特性，并查集的主要用途有以下两点：

1）维护无向图的连通性（判断两个点是否在同一连通块内，或增加一条边后是否会产生环）；

2）用在求解最小生成树的Kruskal算法里。

一般来说，一个并查集对应三个操作：

1、初始化（ Init()函数）

2、查找函数（ Find()函数）

3、合并集合函数（ Join()函数）

综合代码实现

java 复制代码

int  N=1005;		// 指定并查集所能包含元素的个数（由题意决定）
int pre[N];     	// 存储每个结点的前驱结点 
int rank[N];    	// 树的高度 

void init(int n)    // 初始化函数，对录入的 n 个结点进行初始化 
{
    for(int i = 0; i < n; i++){
        pre[i] = i;     			// 每个结点的上级都是自己 
        rank[i] = 1;    			// 每个结点构成的树的高度为 1 
    } 
}

int find(int x)     	 		    // 查找结点 x 的根结点 
{
    if(pre[x] == x) return x;  		// 递归出口：x 的上级为 x 本身，则 x 为根结点 
    return find(pre[x]); 			// 递归查找 
} 
 
int find(int x)    // 改进查找算法：完成路径压缩，将 x 的上级直接变为根结点，那么树的高度就会大大降低 
{
    if(pre[x] == x) return x;		// 递归出口：x 的上级为 x 本身，即 x 为根结点 
    return pre[x] = find(pre[x]);   // 此代码相当于先找到根结点 rootx，然后 pre[x]=rootx 
} 

bool isConnected(int x, int y)      		// 判断两个结点是否连通 
{
    return find(x) == find(y);  	// 判断两个结点的根结点（即代表元）是否相同 
}

bool join(int x,int y)                 // 两个顶点的合并
{
    x = find(x);						// 寻找 x 的代表元
    y = find(y);						// 寻找 y 的代表元
    if(x == y) return false;			// 如果 x 和 y 的代表元一致，说明他们共属同一集合，则不需要合并，返回 false，表示合并失败；否则，执行下面的逻辑
    if(rank[x] > rank[y]) pre[y]=x;		// 如果 x 的高度大于 y，则令 y 的上级为 x
    else								// 否则
    {
        if(rank[x]==rank[y]) rank[y]++;	// 如果 x 的高度和 y 的高度相同，则令 y 的高度加1
        pre[x]=y;						// 让 x 的上级为 y
	}
	return true;						// 返回 true，表示合并成功
}