论文题目:A deep learning-based spatial gradient reconstruction method for efficient damage identification in composite with high-sparsity Lamb wavefield(基于深度学习的高稀疏Lamb波场复合材料损伤有效识别方法)
期刊:Mechanical Systems and Signal Processing
摘要:碳纤维增强塑料(CFRP)的结构完整性和安全性容易受到分层的影响,这往往是肉眼无法察觉的。扫描激光多普勒测振仪(SLDV)在CFRP损伤量化方面显示出良好的前景,但其耗时的测量过程限制了其在工程场景中的应用。为了解决这个问题,我们引入了一种新的损伤指标,即空间梯度,它可以捕捉分层和波场之间的相互作用。我们还开发了一种神经网络,能够直接从以极低的空间采样率获得的高稀疏Lamb波场数据重建空间梯度,从而显着减少测量时间。为了增强网络检测波场异常的能力,我们采用了交叉注意技术,允许将表示局部波场畸变的浅层特征直接注入解码器中。此外,我们集成了多个重建层来指导波场重建过程,确保在每个阶段捕获有意义的信息。与之前的先进技术相比,我们的方法在重建精度方面取得了实质性的改进,在单损伤情况下从70%增加到92%,在多损伤情况下从14%增加到72%。通过空间协方差分析,利用重构的空间梯度场进行损伤成像,验证了该方法在不同损伤位置的可行性和通用性。这表明它有潜力成为快速、准确的损伤表征、减少测量负担和增强实际适用性的可靠解决方案。
深度学习赋能复合材料损伤检测:基于空间梯度重建的高效方法
引言
碳纤维增强塑料(CFRP)因其优异的强度重量比和刚度重量比,在航空航天、汽车和能源等领域得到广泛应用。然而,制造过程中不可避免地会引入微缺陷,在服役条件下可能演变为宏观损伤,其中**分层(Delamination)**是最关键的失效模式之一。分层损伤往往肉眼不可见,但会严重损害结构完整性,甚至导致灾难性失效。
扫描激光多普勒测振仪(SLDV)作为一种非接触式检测技术,能够提供密集的波场数据用于损伤量化,但其测量时间过长的问题一直制约着工程应用。本文介绍的研究正是针对这一挑战,提出了一种创新的解决方案。
一、研究背景与核心问题
1.1 Lamb波检测技术的优势与挑战
Lamb波是一种在板状结构中传播的超声导波,对各类损伤具有高灵敏度,且在复合材料中衰减小。传统的Lamb波检测依赖分布式传感器阵列,而SLDV则通过逐点扫描实现全波场测量,能够直接观察损伤引起的波场异常(如散射波、反射波等)。
然而,问题也随之而来:
┌─────────────────────────────────────────────────────┐
│ SLDV全波场测量的困境 │
├─────────────────────────────────────────────────────┤
│ ▪ 111×111个扫描点 = 12,321个测量点 │
│ ▪ 每个点需要多次平均以降噪 │
│ ▪ 单次全波场测量可能需要数小时 │
│ ▪ 数据存储需求大 │
│ ▪ 严重限制工程效率 │
└─────────────────────────────────────────────────────┘1.2 现有方法的局限性
传统波数分析方法
- 局部波数分析需要进行短空间窗傅里叶变换
- 最优窗口大小的选择是一个悬而未决的难题
- 对操作者经验依赖性强
已有深度学习方法
作者团队此前提出的MAE(Masked AutoEncoder)方法虽然在稀疏波场重建中表现出色,但存在一个关键问题:
"虽然MAE在重建结果与原始结果之间取得了出色的一致性,但其在损伤区域的精度下降,表明在捕获全局传播模式与局部损伤交互细节之间存在不平衡。"
这个问题的本质在于:Transformer架构擅长捕捉全局依赖关系,但容易忽略对损伤识别至关重要的局部细节。
二、创新方案:SFI-MR-MAE框架
2.1 核心创新点概览
本文提出的方法包含三大创新:
┌──────────────────────────────┐
│ SFI-MR-MAE 创新框架 │
└──────────────────────────────┘
│
┌───────────────────────┼───────────────────────┐
▼ ▼ ▼
┌─────────────┐ ┌─────────────────┐ ┌─────────────┐
│ 空间梯度 │ │ 浅层特征注入 │ │ 多阶段重建 │
│ 损伤指标 │ │ (SFI) │ │ (MR) │
└─────────────┘ └─────────────────┘ └─────────────┘
│ 无需基线 │ │ 交叉注意力机制 │ │ 多层监督 │
│ 自参考方法 │ │ 保留局部细节 │ │ 显式引导 │
└─────────────┘ └─────────────────┘ └─────────────┘2.2 空间梯度:一种新型损伤指标
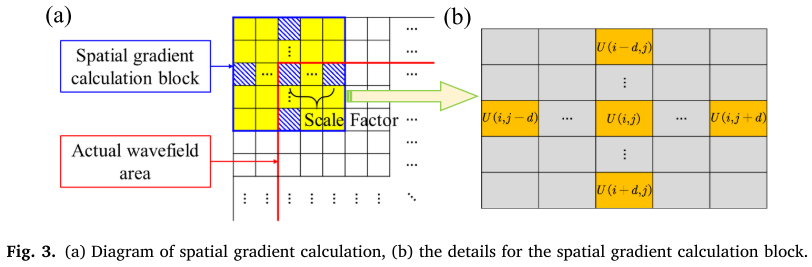
空间梯度的物理意义在于捕捉材料属性的不连续性。当Lamb波通过损伤区域时,会产生局部阻抗失配,导致波场畸变。
空间梯度计算方法:
对于扫描点(i, j)在第t帧的信号U[i,j,t]:
-
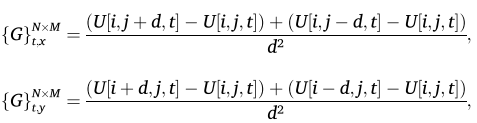
-
总空间梯度 :
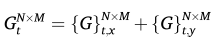
其中,d是空间尺度因子(本文设为2),它决定了空间分辨率与信噪比之间的权衡。
无基线损伤成像的关键步骤:
-
计算相邻时间帧的空间梯度差异:
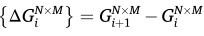
-
对所有时间帧积分得到空间损伤图:
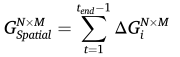
这样做的巧妙之处在于:
- 损伤区域在测量过程中保持静止
- 直接波和反射波随时间移动
- 积分操作使损伤信号累积增强,同时衰减移动波分量
2.3 网络架构详解
整体流程
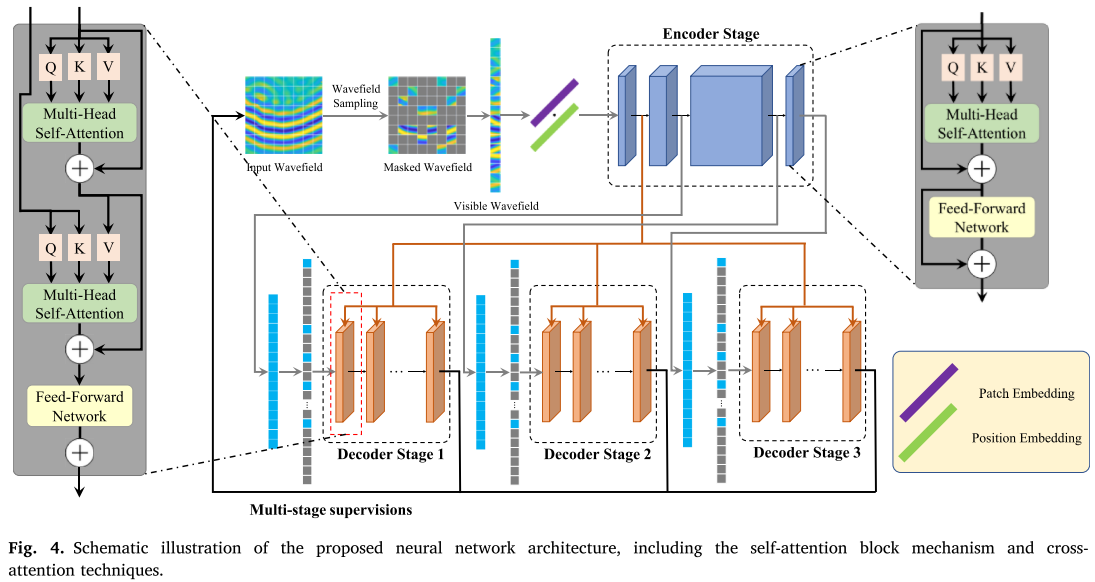
输入稀疏波场 ──┬──> 采样(保留25%) ──> 编码器 ──> 潜在特征
│ │
│ ┌────────────────────┘
│ ▼
│ 浅层特征 ───────────────────────────┐
│ (第一层输出) │
│ ▼
└──────────────────> 解码器 ◄── 交叉注意力注入
│
├── 阶段1重建 ──> Loss₁
├── 阶段2重建 ──> Loss₂
└── 阶段3重建 ──> Loss₃
│
▼
输出:空间梯度图浅层特征注入(SFI)机制
传统的自注意力只处理当前层的特征。本文引入交叉注意力,实现浅层-深层特征融合:
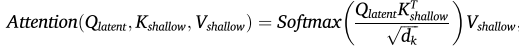
为什么这很重要?
| 特征层级 | 包含信息 | 作用 |
|---|---|---|
| 浅层特征 | 局部波场-损伤交互细节 | 提供精确的空间定位信息 |
| 深层特征 | 全局Lamb波传播模式 | 理解波传播规律 |
通过交叉注意力,解码器能够同时利用两类信息,避免了MAE中"全局有余、局部不足"的问题。
多阶段重建策略
受生物神经网络局部学习机制启发,在多个解码层设置重建目标:
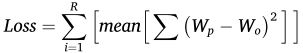
这样做的好处:
- 显式引导各层学习有意义的表示
- 减少训练时的内存开销
- 加速模型收敛
2.4 损伤定位:空间协方差方法
获得空间梯度图后,使用协方差矩阵进行损伤定位:
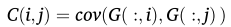
定位原理:
- 协方差矩阵沿对角线对称
- 对角线上的值代表对应空间坐标的方差
- 方差最大值所在位置即为损伤位置
三、实验验证
3.1 实验设置
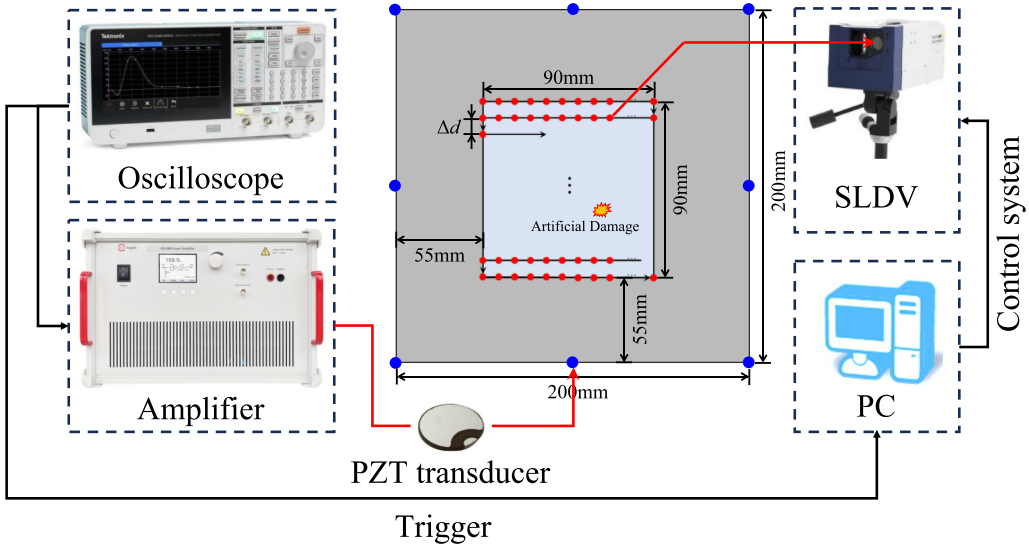
实验配置:
┌────────────────────────────────────────────────┐
│ SLDV: Polytec PSV-500 │
│ 激励信号: 5-500 kHz线性调频信号,持续400μs │
│ 采样频率: 5.12 MHz │
│ 每点平均次数: 40次 │
│ 试件: 450mm × 450mm × 3mm CFRP板 │
│ 铺层顺序: [0 90]₂ₛ │
│ 扫描点数: 111 × 111 = 12,321点 │
│ 模拟损伤: 背面贴附磁铁 │
└────────────────────────────────────────────────┘3.2 数据集划分

| 场景 | 训练集 | 测试集 |
|---|---|---|
| 单损伤(10mm方形) | #1, #2, #3 | #4 |
| 多损伤(10mm+5mm) | #5, #6, #8 | #7 |
采样策略:仅使用**25%**的空间采样点作为网络输入。
3.3 单损伤场景结果
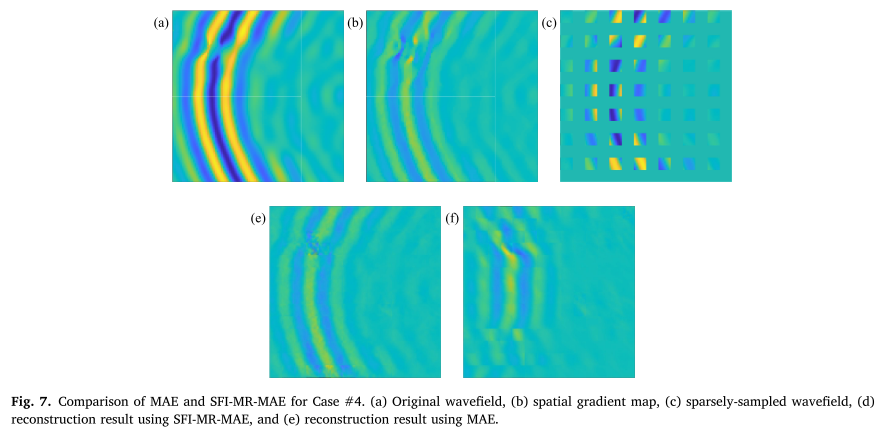
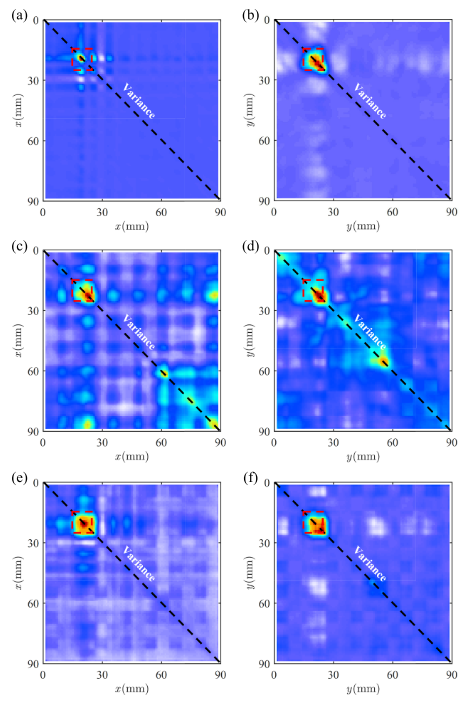
重建精度对比(APL:平均预测损失,越低越好):
| 方法 | 92.58μs | 98.44μs | 所有帧APL | 相对提升 |
|---|---|---|---|---|
| SimMIM | 4.7453 | 4.9678 | 3.8762 | - |
| RDN | 4.0122 | 4.2141 | 2.1415 | - |
| MAE | 3.4952 | 3.5943 | 0.9899 | - |
| SFI-MR-MAE | 0.4268 | 0.5197 | 0.2895 | 70.75% |
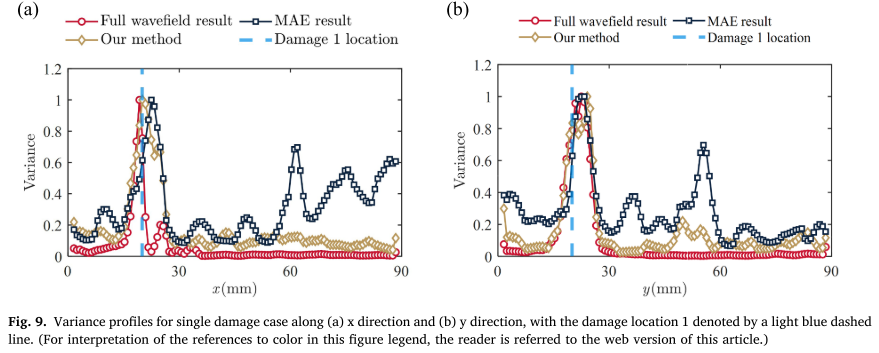
损伤定位精度:
| 方向 | 真实值(mm) | 全波场结果 | MAE结果 | 本文方法 |
|---|---|---|---|---|
| x方向 | 20 | 19.286 | 22.5 | 20.089 |
| y方向 | 20 | 22.5 | 23.303 | 21.696 |
定位误差约0.1-1.7mm,与全波场结果高度一致!
3.4 多损伤场景结果
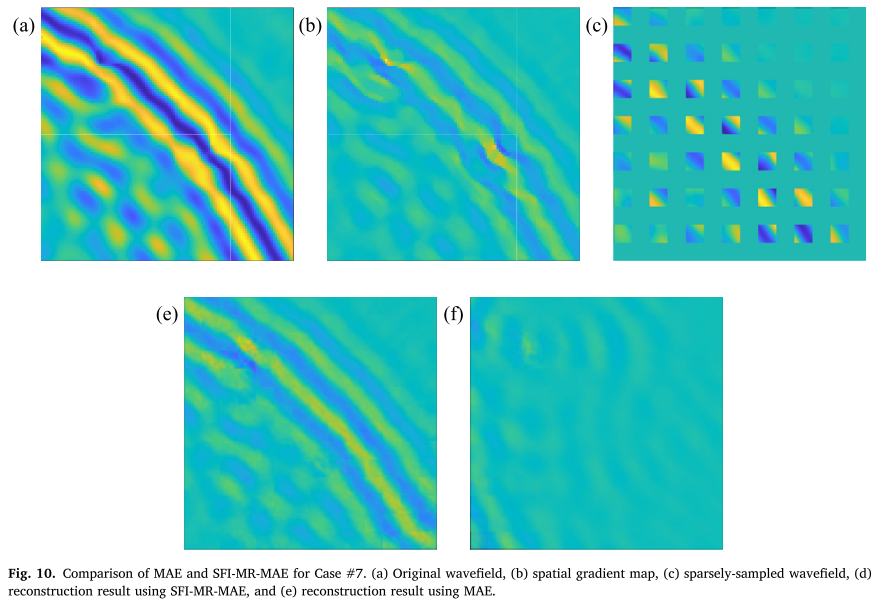
这是更具挑战性的场景,两个损伤相距较近,可能产生相互干扰。
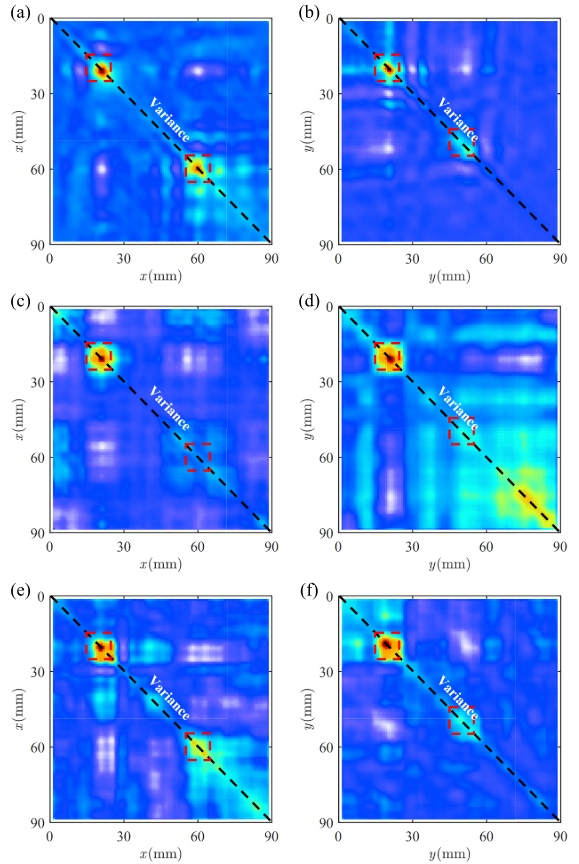
重建精度对比:
| 方法 | APL | 相对提升 |
|---|---|---|
| MAE | 1.3672 | - |
| SFI-MR-MAE | 1.1727 | 14.23% |
虽然提升幅度不如单损伤场景,但关键在于损伤识别能力:
损伤定位对比:
| 损伤 | 方向 | 真实值 | 全波场 | MAE | 本文方法 |
|---|---|---|---|---|---|
| 损伤1 | x | 20mm | 20.893 | 20.893 | 20.089 |
| 损伤1 | y | 20mm | 20.089 | 20.893 | 19.286 |
| 损伤2 | x | 60mm | 60.268 | × | 60.268 |
| 损伤2 | y | 50mm | 40.821 | × | 49.821 |
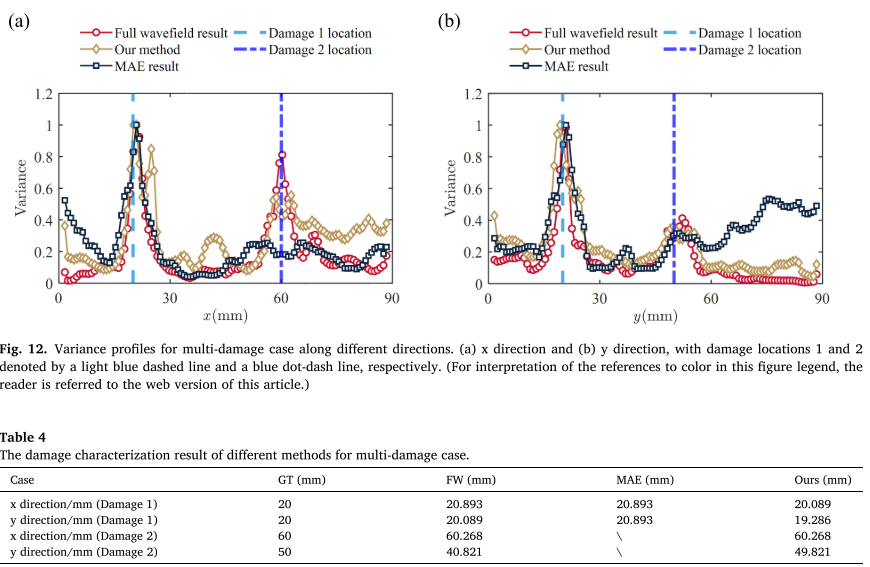
关键发现: MAE无法检测到第二个损伤(表中×表示未检出),而SFI-MR-MAE成功定位了两个损伤!
四、为什么这个方法有效?
4.1 从信息论角度理解
传统MAE的问题:
┌─────────────────────────────────────────────┐
│ 编码器深层 │
│ ┌─────────────────┐ │
│ │ 全局传播模式 │ ✓ 充分学习 │
│ │ (结构知识) │ │
│ └─────────────────┘ │
│ ┌─────────────────┐ │
│ │ 局部损伤细节 │ ✗ 信息丢失 │
│ │ (上下文信息) │ │
│ └─────────────────┘ │
└─────────────────────────────────────────────┘
SFI-MR-MAE的解决方案:
┌─────────────────────────────────────────────┐
│ 编码器浅层 ─────────────────┐ │
│ ┌─────────────────┐ │ 交叉注意力 │
│ │ 局部损伤细节 │ ───────┼────────> │
│ └─────────────────┘ │ 注入解码器 │
│ │ │
│ 编码器深层 ▼ │
│ ┌─────────────────┐ ┌────────────┐ │
│ │ 全局传播模式 │ ──>│ 特征融合 │ │
│ └─────────────────┘ └────────────┘ │
│ │
│ ➜ 两类信息协同工作,实现精确重建 │
└─────────────────────────────────────────────┘4.2 多阶段重建的作用
传统端到端训练只在最后一层计算损失,梯度需要通过所有层反向传播,导致:
- 底层网络梯度消失
- 中间层表示学习不充分
多阶段重建相当于在网络中设置多个"检查点",确保每个阶段都在学习有意义的表示。
五、实际应用价值
5.1 效率提升
| 指标 | 传统方法 | 本文方法 | 提升 |
|---|---|---|---|
| 空间采样率 | 100% | 25% | 4倍减少 |
| 测量时间 | ~数小时 | ~1/4原时间 | 4倍加速 |
| 定位精度 | 基准 | 接近基准 | 基本保持 |
5.2 三大优势
- 无需专家经验:自动化损伤定位流程
- 大幅缩短测量时间:使SLDV应用于工业场景成为可能
- 无需基线数据:不需要预先测量无损伤状态
5.3 潜在应用场景
- 航空航天结构健康监测
- 风力发电叶片检测
- 汽车复合材料部件质检
- 在线快速损伤筛查
六、未来展望
作者指出了几个值得探索的方向:
- 超参数优化:进一步提升重建精度
- 自适应阈值:通过设置协方差矩阵对角线阈值实现自动损伤量化
- 跨结构泛化:将方法应用于更多结构类型和损伤场景
- 多传感器融合:与声发射等技术结合,构建综合监测系统
总结
这篇论文的核心贡献在于:
通过引入空间梯度 作为损伤敏感指标,结合浅层特征注入 和多阶段重建策略,实现了从仅25%采样率的稀疏波场数据中高精度重建空间梯度,并成功进行无基线损伤定位。
这不仅是一个技术上的突破,更是将实验室技术向工程应用推进的重要一步。当测量时间从数小时缩短到一小时以内时,SLDV技术才能真正走出实验室,服务于工业生产线上的快速检测需求。