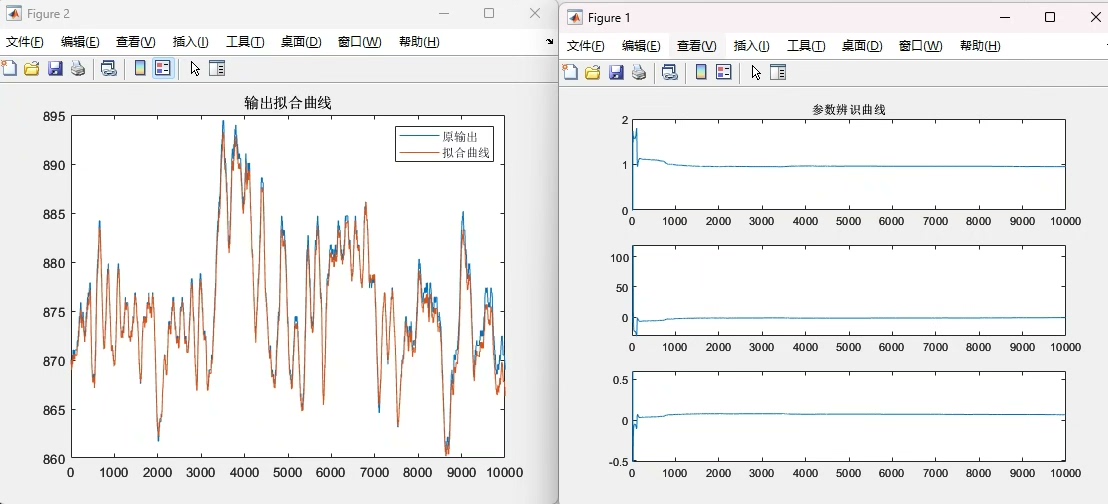
MATLAB多变量最小二乘辨识

matlab多变量最小二乘辨识

多变量最小二乘在系统辨识里算是老熟人了，咱们今天直接上Matlab整点实在的。先来个简单场景：假设有个双输入双输出系统，输出受白噪声干扰，咱们要通过输入输出数据把系统模型给扒出来。

先造点测试数据热身。假设真实系统模型是：

matlab 复制代码

% 真实参数矩阵
Theta_true = [0.8  -0.2; 
              0.1  0.6];
n = 1000;  % 数据点数
U = randn(n, 2);  % 输入信号
Y = zeros(n, 2);  % 输出信号

% 生成输出数据（带噪声）
for k = 2:n
    Y(k,:) = Y(k-1,:)*Theta_true' + U(k,:) + 0.5*randn(1,2);
end

这段代码故意留了个坑------生成数据时用了上一时刻的输出和当前输入，这会影响后续数据矩阵的构造。注意看Y的计算方式，后面构建H矩阵时要对应这个结构。

关键环节来了，构造数据矩阵：

matlab 复制代码

% 构建H矩阵
H = zeros(n-1, 4);  % 两输出，每个方程两个参数
for k = 2:n
    H(k-1, :) = [Y(k-1,1), Y(k-1,2), U(k,1), U(k,2)];
end

% 参数估计
Theta_hat = H \ Y(2:end, :)';

这里H矩阵的列对应[y1(k-1), y2(k-1), u1(k), u2(k)]，和生成数据的公式严格对应。Matlab的反斜杠运算符直接搞定最小二乘，但要注意维度对齐------Y需要转置并去掉第一个数据点。

验证环节不能少：

matlab 复制代码

% 计算拟合优度
Y_pred = H * Theta_hat;
R_squared = 1 - sum((Y(2:end,:) - Y_pred').^2) ./ sum((Y(2:end,:) - mean(Y)).^2)

% 参数对比
disp('真实参数矩阵:')
disp(Theta_true)
disp('估计参数矩阵:')
disp(Theta_hat')

R平方值超过0.8基本能看，但要注意残差的白噪声检验。有时候会遇到矩阵病态问题，可以加个正则化：

matlab 复制代码

% 带正则化的岭回归
lambda = 0.1;  % 正则化系数
Theta_hat_ridge = (H'*H + lambda*eye(4)) \ (H'*Y(2:end,:));

实际调试时得注意输入信号的持续激励性------别用全零或周期重复的信号。遇到过个坑，输入信号幅值太小导致数值计算不稳定，后来加了个数据标准化才解决：

matlab 复制代码

% 数据标准化
U_normalized = (U - mean(U)) ./ std(U);
Y_normalized = (Y - mean(Y)) ./ std(Y);

最后提醒下，多变量情况要注意输入输出的延迟匹配。曾经有个项目因为u(k)和y(k+1)的时序没对齐，参数估计直接跑偏到姥姥家了。代码里的时间索引建议画个时序图确认清楚再开跑。