六相永磁同步电机矢量控制仿真模型探索

六相永磁同步电机矢量控制仿真模型

在电机控制领域，六相永磁同步电机（PMSM）凭借其高功率密度、良好的容错性能等优势，逐渐成为研究热点。而矢量控制作为一种先进的电机控制策略，能有效实现对电机转矩和磁链的解耦控制，让电机性能更加出色。今天咱们就来聊聊六相永磁同步电机矢量控制仿真模型那些事儿。

矢量控制原理

矢量控制的核心思想是将交流电机的定子电流分解成产生磁场的励磁分量和产生转矩的转矩分量，并分别加以控制，从而实现类似于直流电机的控制效果。对于六相永磁同步电机，我们通常采用坐标变换的方法，将三相静止坐标系下的电流转换到两相旋转坐标系（d - q 坐标系）下。

下面是一段简单的 Python 代码示例，用于实现三相到两相的克拉克变换（Clarke Transformation）：

python 复制代码

import numpy as np

def clarke_transformation(ia, ib, ic):
    """
    克拉克变换，将三相静止坐标系下的电流转换到两相静止坐标系下
    :param ia: 相电流 A
    :param ib: 相电流 B
    :param ic: 相电流 C
    :return: 两相静止坐标系下的电流 alpha 和 beta
    """
    i_alpha = (2/3) * (ia - 0.5 * ib - 0.5 * ic)
    i_beta = (np.sqrt(3)/3) * (ib - ic)
    return i_alpha, i_beta

# 示例数据
ia = 1.0
ib = 0.5
ic = -1.5

i_alpha, i_beta = clarke_transformation(ia, ib, ic)
print(f"i_alpha: {i_alpha}, i_beta: {i_beta}")

代码分析：这段代码定义了一个 clarketransformation**函数，它接受三相电流 ia、ib、ic 作为输入，通过克拉克变换公式计算出两相静止坐标系下的电流 i alpha 和 i_beta。在实际应用中，我们可以利用这个变换将三相电流转换到两相坐标系，方便后续的控制算法设计。

仿真模型搭建

在搭建六相永磁同步电机矢量控制仿真模型时，我们通常会使用专业的仿真软件，如 MATLAB/Simulink。下面是一个简单的 Simulink 模型搭建步骤：

电机模型：在 Simulink 中选择合适的六相永磁同步电机模块，设置电机的参数，如定子电阻、电感、永磁体磁链等。
坐标变换模块：添加克拉克变换和帕克变换（Park Transformation）模块，将三相电流转换到 d - q 坐标系。
控制器模块：设计速度控制器和电流控制器，如 PI 控制器，用于控制电机的速度和电流。
逆变器模块：添加逆变器模块，将直流电压转换为交流电压，驱动电机运行。

下面是一段简单的 MATLAB 代码，用于实现 PI 控制器：

matlab 复制代码

% PI 控制器参数
Kp = 1.0;
Ki = 0.1;

% 误差积分项
integral_error = 0;

% 设定值和反馈值
setpoint = 10;
feedback = 5;

% 计算误差
error = setpoint - feedback;

% 积分项更新
integral_error = integral_error + error;

% 计算控制输出
output = Kp * error + Ki * integral_error;

disp(['PI 控制器输出: ', num2str(output)]);

代码分析：这段 MATLAB 代码实现了一个简单的 PI 控制器。通过设定比例系数 Kp 和积分系数 Ki，计算误差并更新积分项，最终得到控制输出。在实际的仿真模型中，我们可以将这个 PI 控制器应用到速度控制和电流控制环节。

仿真结果分析

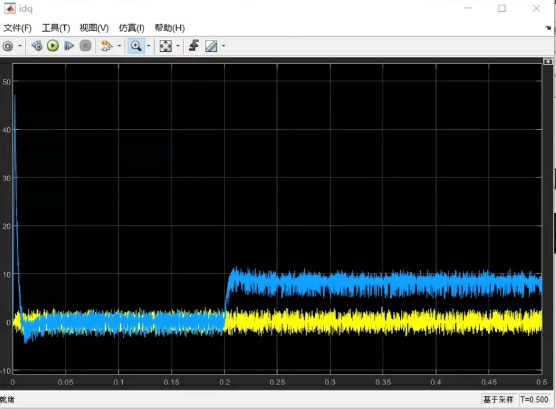
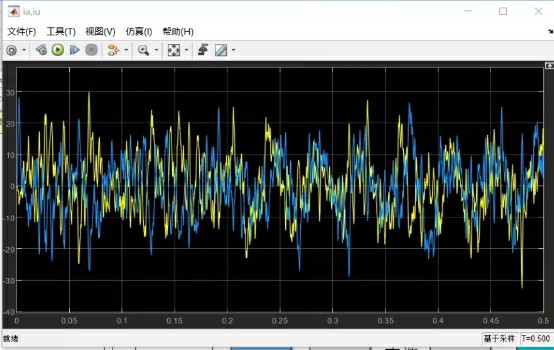
搭建好仿真模型后，我们可以进行仿真实验，观察电机的运行性能。通过分析仿真结果，如电机的转速、转矩、电流等波形，我们可以评估矢量控制策略的有效性。

例如，如果电机的转速能够快速跟踪设定值，并且转矩波动较小，说明矢量控制策略能够有效地控制电机的运行。反之，如果出现转速超调、转矩波动较大等问题，我们就需要调整控制器的参数，优化控制策略。

总之，六相永磁同步电机矢量控制仿真模型是研究和开发电机控制系统的重要工具。通过合理的模型搭建和参数调整，我们可以实现对电机的高效、精确控制，为实际应用提供有力的支持。希望这篇文章能让你对六相永磁同步电机矢量控制仿真模型有更深入的了解。