无人船、AUV与无人车编队路径跟踪的奇妙探索

无人船，AUV，无人车编队路径跟踪领航跟随los制导反步控制路径可调，模型可调 MATLAB程序

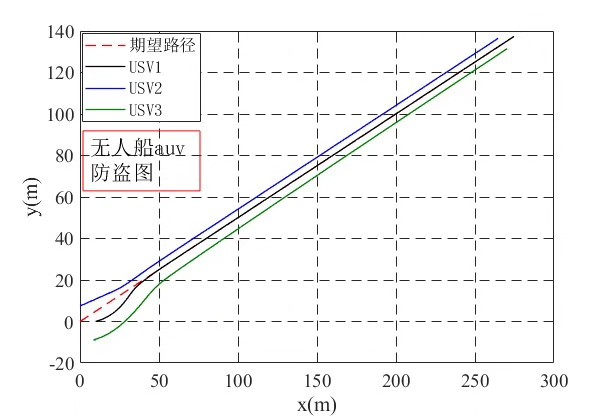
在自动化载具的领域中，无人船、AUV（自主水下航行器）以及无人车的编队路径跟踪是一个极富挑战与魅力的研究方向。今天咱就来唠唠基于领航跟随LOS（视线法）制导结合反步控制的实现，还得让路径和模型都能灵活调整，最后通过MATLAB程序来一展身手。

领航跟随LOS制导

LOS制导就像是给编队里的"小弟"们指了一条明路。想象一下，领航者在前面跑，跟随者得时刻盯着领航者，按照一定的规则去追。具体来讲，跟随者要保持和领航者之间有一条虚拟的视线（Line - of - Sight）。咱们来看段简单的代码示例（假设二维平面情况）：

matlab 复制代码

% 假设领航者位置
leader_x = 10; 
leader_y = 10; 
% 跟随者位置
follower_x = 5; 
follower_y = 5; 
% LOS向量计算
LOS_vector_x = leader_x - follower_x; 
LOS_vector_y = leader_y - follower_y; 
distance = sqrt(LOS_vector_x^2 + LOS_vector_y^2);

在这段代码里，我们先设定了领航者和跟随者的位置，然后通过计算两者坐标差值得到LOS向量，并且算出了两者之间的距离。这距离和LOS向量方向对于跟随者调整自己的路径至关重要。

反步控制

反步控制是一种逐步构建控制律的方法，就像搭积木一样，一步一步把复杂的控制系统搭建起来。比如说，我们先对系统的一部分设计一个虚拟控制输入，然后基于这个虚拟输入，再为整个系统设计实际的控制输入。代码实现起来大概是这样：

matlab 复制代码

% 假设系统状态变量
x = [1; 0]; % 例如 [位置; 速度]
% 第一步：设计虚拟控制输入
alpha1 = -x(1); % 简单示例，根据系统期望输出设计
% 第二步：设计实际控制输入
u = -x(2) - alpha1;

这里先定义了系统的状态变量，然后第一步设计了虚拟控制输入alpha1，它是基于系统的位置状态x(1)来设定的，目的是让系统朝着期望的位置变化。接着，在第二步根据虚拟控制输入和速度状态x(2)设计了实际的控制输入u，让系统能够按照我们设想的方式运行。

路径与模型可调

要实现路径可调，我们可以通过修改领航者的路径规划来达到目的。比如说，领航者原本是直线行驶，我们可以通过改变其目标点的设定，让它走曲线。对于模型可调，我们可以改变系统动力学模型中的参数。假设我们有一个简单的无人车动力学模型：

matlab 复制代码

% 无人车动力学模型参数
m = 100; % 质量
C_d = 0.3; % 阻力系数
% 改变模型参数，例如改变质量
m_new = 150;

这里先设定了原始的模型参数，然后可以轻松地改变质量m的值，来调整无人车的动力学模型，进而影响其运动特性。

MATLAB完整程序示例

matlab 复制代码

% 初始化参数
num_followers = 3; % 跟随者数量
time_step = 0.1; % 时间步长
total_time = 100; % 总模拟时间
% 初始化领航者路径
leader_path_x = zeros(1, total_time/time_step + 1); 
leader_path_y = zeros(1, total_time/time_step + 1); 
leader_path_x(1) = 0; 
leader_path_y(1) = 0; 
for i = 2:length(leader_path_x)
    leader_path_x(i) = leader_path_x(i - 1) + 0.5; % 简单直线运动示例，可调整为复杂路径
    leader_path_y(i) = leader_path_y(i - 1); 
end
% 初始化跟随者位置
follower_positions_x = zeros(num_followers, total_time/time_step + 1); 
follower_positions_y = zeros(num_followers, total_time/time_step + 1); 
follower_positions_x(:,1) = [-2; -4; -6]; 
follower_positions_y(:,1) = [0; 0; 0]; 
for t = 2:length(leader_path_x)
    for j = 1:num_followers
        % LOS制导计算
        LOS_vector_x = leader_path_x(t) - follower_positions_x(j,t - 1); 
        LOS_vector_y = leader_path_y(t) - follower_positions_y(j,t - 1); 
        distance = sqrt(LOS_vector_x^2 + LOS_vector_y^2); 
        % 反步控制计算
        % 假设简单动力学模型，此处省略详细推导
        u_x = -follower_positions_x(j,t - 1) + LOS_vector_x/distance; 
        u_y = -follower_positions_y(j,t - 1) + LOS_vector_y/distance; 
        follower_positions_x(j,t) = follower_positions_x(j,t - 1) + u_x * time_step; 
        follower_positions_y(j,t) = follower_positions_y(j,t - 1) + u_y * time_step; 
    end
end
% 绘图
figure; 
hold on; 
plot(leader_path_x, leader_path_y, 'r', 'LineWidth', 2); 
for j = 1:num_followers
    plot(follower_positions_x(j,:), follower_positions_y(j,:), 'b--'); 
end
xlabel('X position'); 
ylabel('Y position'); 
legend('Leader', 'Follower 1', 'Follower 2', 'Follower 3'); 
title('Formation Path Tracking');

这个完整的MATLAB程序，首先初始化了各种参数，包括跟随者数量、时间步长等。接着设定了领航者的路径，这里是简单的直线运动，你完全可以改成复杂的曲线等路径。然后对跟随者位置进行初始化，在主循环里，通过LOS制导和反步控制计算出每个跟随者下一时刻的位置，最后通过绘图展示出领航者和跟随者的运动轨迹。

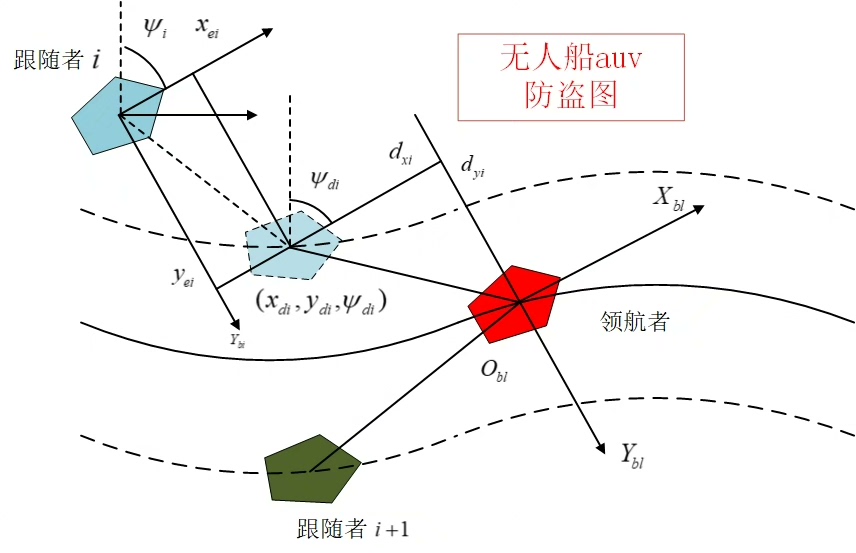
无人船、AUV和无人车的编队路径跟踪充满了无限可能，通过LOS制导、反步控制以及灵活可调的路径与模型，再借助MATLAB强大的计算和绘图能力，我们能不断探索这个有趣的领域，为未来自动化载具的协同作业打下坚实基础。