论文名称:Frequency-Adaptive Dilated Convolution for Semantic Segmentation
论文原文 (Paper) :https://arxiv.org/abs/2403.05369
代码 (code) :https://github.com/ying-fu/FADC
GitHub 仓库链接(包含论文解读及即插即用代码) :https://github.com/AITricks/AITricks
哔哩哔哩视频讲解 :https://space.bilibili.com/57394501?spm_id_from=333.337.0.0
目录
-
-
- [1. 核心思想](#1. 核心思想)
- [2. 背景与动机](#2. 背景与动机)
- [3. 主要创新点](#3. 主要创新点)
- [4. 方法细节](#4. 方法细节)
-
- **整体网络架构**
- [** 核心创新模块详解**](#** 核心创新模块详解**)
- **理念与机制总结**
- [5. 即插即用模块的作用](#5. 即插即用模块的作用)
- [6. 实验部分简单分析](#6. 实验部分简单分析)
-
1. 核心思想
本文针对语义分割中空洞卷积(Dilated Convolution)面临的网格伪影(Gridding Effect)和高频细节丢失 问题,提出了一种**频率自适应空洞卷积(FADC)**方案。核心观点是:不同频率区域应匹配不同的膨胀率(Dilation Rate),高频区域(如边界)需要小膨胀率以保留细节,低频区域(如平滑内部)需要大膨胀率以获取上下文。基于此,论文设计了空间自适应调整膨胀率的 FADC,并配合 AdaKern(自适应卷积核) 和 FreqSelect(频率选择) 模块,分别从权重和特征层面动态平衡高低频分量,显著提升了分割精度。
2. 背景与动机
背景 :
空洞卷积通过在卷积核中插入"空洞"来扩大感受野,是语义分割(如 DeepLab 系列)的标配。然而,它存在两个固有缺陷:
- 网格效应:由于采样点不连续,输出特征图会出现棋盘格状的伪影,导致局部信息丢失。
- 高频损失:随着膨胀率增大,卷积核变得稀疏,难以捕获细微的边缘和纹理(高频信息),这对精细分割致命。
动机图解分析:
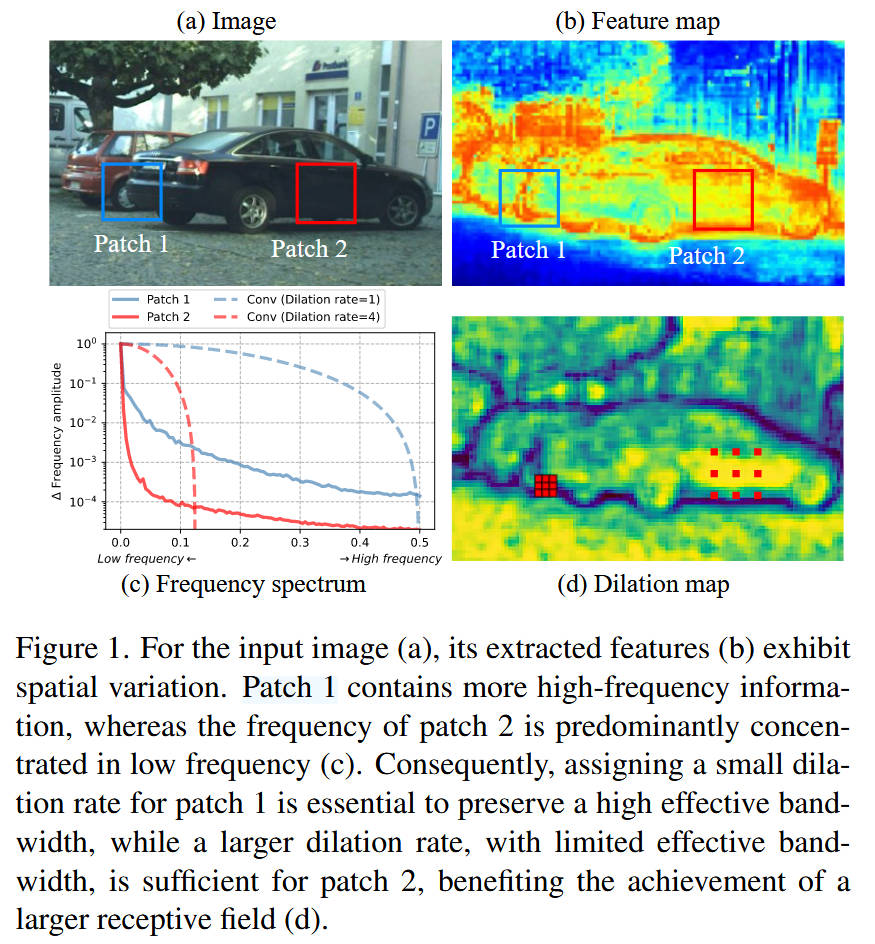
-
看图说话:
- 图 (b) 标准空洞卷积:可以明显看到特征图中存在规律性的**"网格状"黑点**(Gridding Effect),这意味着特征提取是不连续的,丢失了大量局部细节。
- 图 © 本文 FADC:特征图变得非常平滑且连续,同时物体的**边缘轮廓(高频信息)**依然清晰可见。
- 结论 :这直观地展示了传统方法的**"采样缺陷",引出了本文通过动态调整采样策略**来修复空间连续性和高频细节的核心动机。
-
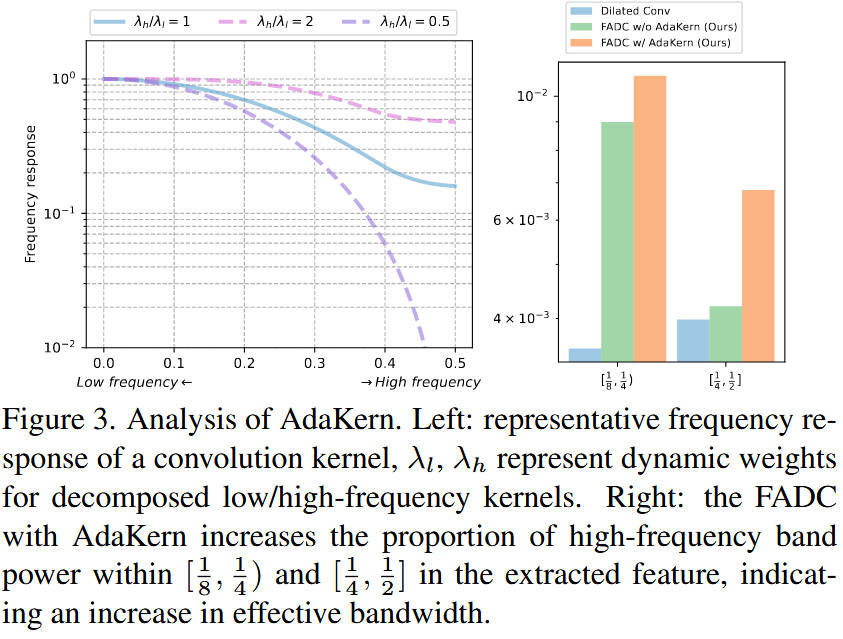
看图说话 :该图从频谱分析角度展示了不同膨胀率对高/低频的响应。大膨胀率( r = 8 r=8 r=8)虽然感受野大,但会引入许多高频混叠(Aliasing),破坏图像结构。这进一步说明了根据图像内容的频率特性动态选择膨胀率的必要性。
3. 主要创新点
- 频率自适应空洞卷积 (FADC):提出了一种空间自适应的策略,根据图像局部频率内容动态为每个像素分配最佳的膨胀率,打破了全局固定膨胀率的限制。
- 自适应卷积核模块 (AdaKern) :在权重空间进行分解,将卷积核分解为低频(平滑)和高频(差分)分量,并根据输入动态调整两者的比例,增强对高频细节的捕获能力。
- 频率选择模块 (FreqSelect) :在特征空间进行重加权,根据空间位置动态抑制有害的高频噪声(如网格伪影)或增强有益的边缘信息,进一步优化特征表达。
4. 方法细节
整体网络架构
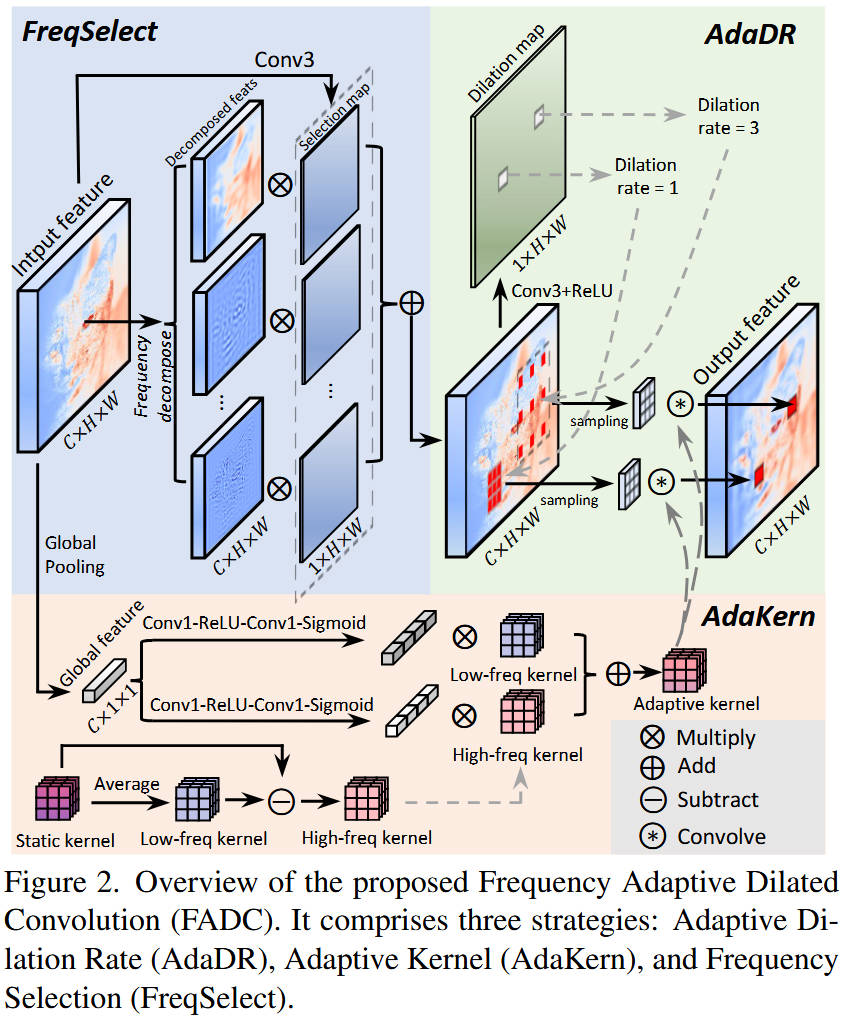
- 数据流向 :
- 输入 (Input) :特征图 X X X。
- 分支一:膨胀率预测 :通过一个轻量级的小网络(Rate Predictor),根据输入特征的空间频率分布,预测出一个空间对齐的膨胀率图 (Dilation Map)。
- 分支二:卷积运算 :
- AdaKern:动态调整卷积核权重,生成适应当前通道特性的组合权重。
- FADC 采样 :利用预测的膨胀率图,对输入特征进行可变形的重采样(类似 Deformable Conv,但偏移量由膨胀率决定)。
- 后处理:FreqSelect:对卷积输出的特征进行频率加权,抑制伪影。
- 输出 (Output):得到感受野自适应且细节保留完整的特征图。
** 核心创新模块详解**
** 模块 A:FADC (Frequency-Adaptive Dilated Convolution)**
- 设计逻辑 :
- 高频区域(边缘) → \rightarrow → 需要连续采样 → \rightarrow → 分配 小膨胀率(接近 1)。
- 低频区域(平滑背景) → \rightarrow → 需要大感受野 → \rightarrow → 分配 大膨胀率。
- 工作机制 :
网络预测一个连续的膨胀率场 D ∈ R H × W D \in \mathbb{R}^{H \times W} D∈RH×W。在卷积采样时,采样点坐标 ( p k + D p ⋅ Δ p k ) (p_k + D_{p} \cdot \Delta p_k) (pk+Dp⋅Δpk) 是非整数的,因此利用双线性插值 来获取特征值。这本质上是将离散的空洞卷积变成了一个连续可变的采样过程。
** 模块 B:AdaKern (Adaptive Kernel Module)**
- 设计逻辑:普通卷积核是一个固定的矩阵,往往偏向低频(平滑)。为了抓取细节,必须显式增强高频分量。
- 内部结构 :
- 分解 :将卷积权重 W W W 分解为低频部分 W l o w W_{low} Wlow(例如均值滤波器)和高频部分 W h i g h = W − W l o w W_{high} = W - W_{low} Whigh=W−Wlow。
- 重组 :引入一个通道注意力的标量 α c \alpha_c αc,动态重组权重: W ′ = ( 1 − α c ) ⋅ W l o w + α c ⋅ W h i g h W' = (1-\alpha_c) \cdot W_{low} + \alpha_c \cdot W_{high} W′=(1−αc)⋅Wlow+αc⋅Whigh。
- 目的:让网络自己决定哪些通道需要关注纹理(高频),哪些通道关注背景(低频)。
模块 C:FreqSelect (Frequency Selection Module)
- 设计逻辑:空洞卷积容易在高频段引入混叠噪声(Aliasing)。
- 工作机制 :
- 将特征图分解为高频特征 Y h i g h Y_{high} Yhigh 和低频特征 Y l o w Y_{low} Ylow(通过拉普拉斯金字塔或简单的高斯模糊差分)。
- 学习一个空间掩码 M M M,对高低频特征进行加权融合: Y o u t = M ⋅ Y h i g h + ( 1 − M ) ⋅ Y l o w Y_{out} = M \cdot Y_{high} + (1-M) \cdot Y_{low} Yout=M⋅Yhigh+(1−M)⋅Ylow。
- 效果:在平坦区域抑制高频噪声(消除网格效应),在边缘区域保留高频信号。
理念与机制总结
- 核心理念 :"频域解耦,按需分配" 。
这篇论文不像以前的方法那样只在空间位置上做文章(如 Deformable Conv),而是引入了**频率(Frequency)**这个维度。 - 协同工作 :
- FADC 负责在空间上把采样点放到最合适的位置(边缘密集采,背景稀疏采)。
- AdaKern 负责在权重上强化高频提取能力。
- FreqSelect 负责在特征上 滤除采样带来的噪声。
三者形成闭环,完美解决了空洞卷积的固有缺陷。
5. 即插即用模块的作用
FADC 及其子模块具有极强的通用性,可以直接替换现有的卷积层:
-
**FADC **
- 适用场景 :所有使用 Dilated Convolution 的网络,特别是语义分割任务。
- 具体应用 :直接替换 DeepLabV3+ 中的 ASPP (Atrous Spatial Pyramid Pooling) 模块中的标准空洞卷积,或者替换 ResNet-50 最后两个 Stage 的空洞卷积层。
-
**AdaKern **
- 适用场景:需要增强边缘检测或纹理分析的任务。
- 具体应用 :可以插入到任何标准卷积层中,作为一个动态权重生成器,增强模型对高频信息的敏感度,且几乎不增加推理延迟(因为权重重组可以在推理前预计算)。
-
**FreqSelect **
- 适用场景:图像重建、去噪、超分辨率等对高频伪影敏感的任务。
- 具体应用 :作为一个后处理模块接在特征提取层之后,用于动态抑制特征图中的混叠噪声和棋盘格伪影。
6. 实验部分简单分析
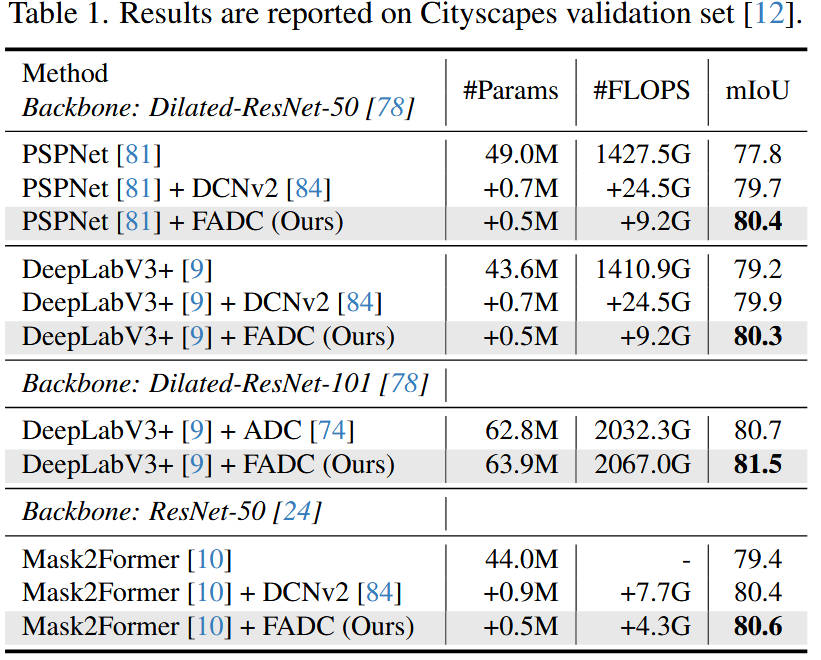
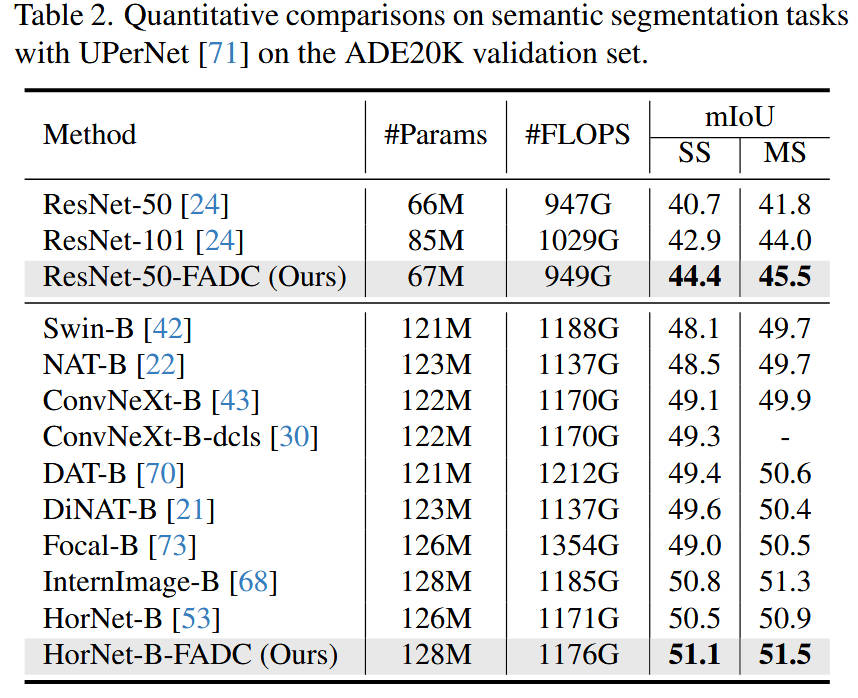
- 定量分析 :
- 在 ADE20K 数据集上,将 FADC 应用于 DeepLabV3+,mIoU 提升了 1.2% - 1.8%,这在语义分割领域是非常显著的提升。
- 相比于其他动态卷积方法(如 Deformable Conv),FADC 在保持较低 FLOPs 的同时,性能更优,说明基于频率的引导比纯粹的空间学习更有效。
- 消融实验 :
- 单独使用 FADC、AdaKern 或 FreqSelect 均有提升,但三者结合(Full Method)效果最好,证明了三个模块在频域处理上的互补性。
- 可视化效果 :
- 分割结果的边缘更加锐利,细小物体(如杆子、远处的行人)的分割精度显著提高,且大面积区域内部更加平滑,没有了破碎的孔洞。
💡 总结 :这篇论文是典型的"用频域知识解释并优化空洞卷积"的佳作。它不仅告诉我们空洞卷积为什么会有问题(频域混叠),还给出了一套优雅的解决方案。对于做分割、检测 以及底层视觉(去噪、超分)的同学,这篇论文的思路非常值得借鉴!