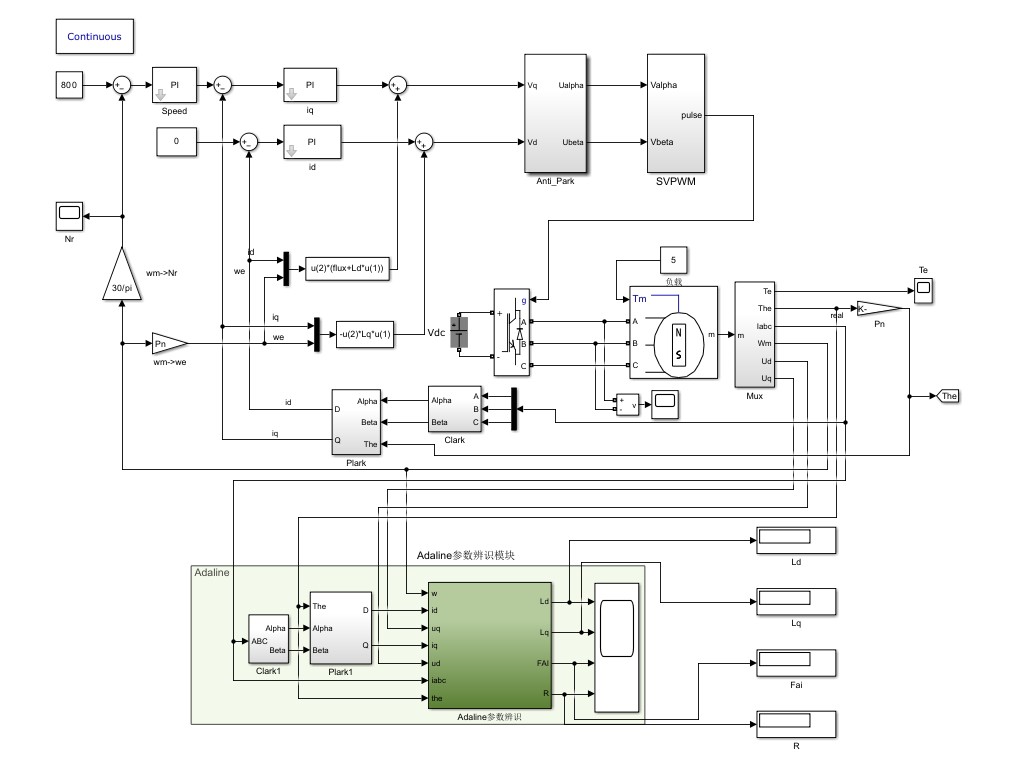
永磁同步电机参数辨识那些事儿

永磁同步电机参数辨识，注入法参数辨识，自适应神经网络法参数辨识，定子电阻，直轴电感，交轴电感，磁链在线辨识

在永磁同步电机（PMSM）的控制领域中，参数辨识可是个至关重要的环节。准确获取电机的各项参数，如定子电阻、直轴电感、交轴电感以及磁链等，对于提升电机控制性能、优化运行效率都起着关键作用。今天咱们就来唠唠永磁同步电机参数辨识中的注入法参数辨识和自适应神经网络法参数辨识。

注入法参数辨识

注入法参数辨识是一种常用的手段。简单来说，它是通过向电机系统中注入特定的信号，然后根据电机的响应来确定相关参数。

以定子电阻的辨识为例，假设我们注入一个高频电压信号 $u*{h}$ ，对应的电流响应为 $i*{h}$ 。在一定的假设条件下，定子电阻 $R_{s}$ 可以通过以下近似公式计算：

python 复制代码

# 假设已经获取到高频电压u_h和电流i_h
u_h = 10  # 这里假设高频电压值为10V
i_h = 2   # 这里假设高频电流值为2A
Rs = u_h / i_h
print("定子电阻Rs估计值为:", Rs, "Ω")

上述代码中，我们模拟了通过测量高频电压和电流来计算定子电阻的过程。实际应用中，这些测量值需要从电机的实际运行数据中获取，并且可能需要经过一些滤波等预处理操作以提高数据准确性。

对于直轴电感 $L*d$ 和交轴电感 $L* q$ 的辨识，注入法通常会利用高频旋转电压信号。在dq坐标系下，根据电机的电压方程和电流响应之间的关系，可以建立相应的数学模型来求解电感值。比如，通过注入一个高频正弦电压信号 $u*{h}(t) = U*{h}sin(\\omega_{h}t)$ ，并监测dq轴电流响应，经过一系列复杂的推导（这里省略详细的数学推导过程，毕竟咱们不是写学术论文嘛），可以得到电感的计算公式。

python 复制代码

# 实际代码实现中，需要对测量到的电流、电压数据进行处理
# 这里简单假设已经得到了用于计算Ld和Lq的相关数据
# 假设已经计算得到的中间变量
alpha = 0.5
beta = 0.3
Ud = 5  # d轴电压
Uq = 4  # q轴电压
Id = 1  # d轴电流
Iq = 1.2  # q轴电流
Ld = (Ud - alpha * Id) / (beta * Iq)
Lq = (Uq - alpha * Iq) / (beta * Id)
print("直轴电感Ld估计值为:", Ld, "H")
print("交轴电感Lq估计值为:", Lq, "H")

这段代码模拟了根据测量数据计算直轴电感和交轴电感的过程。实际应用中，数据处理和算法实现会更为复杂，还需要考虑电机运行状态的变化等多种因素。

自适应神经网络法参数辨识

自适应神经网络法参数辨识则是利用神经网络强大的非线性映射能力来对永磁同步电机参数进行估计。神经网络可以根据输入的电机运行数据（如电压、电流、转速等），通过不断调整自身的权重和阈值，来逼近真实的参数值。

假设我们构建一个简单的三层神经网络来辨识磁链。输入层接收电机的电压和电流信号，隐含层通过非线性激活函数对输入进行处理，输出层则输出磁链的估计值。

python 复制代码

import numpy as np


# 定义激活函数sigmoid
def sigmoid(x):
    return 1 / (1 + np.exp(-x))


# 初始化神经网络参数
input_size = 2  # 输入层节点数，对应电压和电流
hidden_size = 5  # 隐含层节点数
output_size = 1  # 输出层节点数，对应磁链

weights_ih = np.random.randn(input_size, hidden_size)
weights_ho = np.random.randn(hidden_size, output_size)

# 假设获取到的输入数据
voltage = 220
current = 5
input_data = np.array([[voltage, current]])

# 前向传播
hidden_layer = sigmoid(np.dot(input_data, weights_ih))
output_layer = sigmoid(np.dot(hidden_layer, weights_ho))
estimated_flux = output_layer[0][0]
print("估计的磁链值为:", estimated_flux)

在上述代码中，我们简单构建了一个神经网络并进行了前向传播计算。实际应用中，还需要大量的训练数据来调整神经网络的权重，常用的方法如梯度下降法，以最小化估计值与真实值之间的误差。通过不断迭代训练，使得神经网络能够准确地辨识出磁链值。

永磁同步电机参数辨识的注入法和自适应神经网络法各有千秋。注入法相对原理清晰，实现相对直接，但对信号注入和测量要求较高；自适应神经网络法具有强大的非线性处理能力，能够适应复杂的电机运行工况，但训练过程较为复杂，计算量较大。在实际应用中，我们需要根据具体的需求和场景来选择合适的辨识方法，以实现对永磁同步电机参数的精准在线辨识，让电机运行得更加高效稳定。