31 Reinforcement Learning Introduction
31.1 What is Reinforcement Learning?
强化学习 (RL) 是一种让 智能体(Agent) 通过与 环境(Environment) 的不断交互来学习最优行为策略的方法
- 目标 : 最大化在长期内获得的累计奖励(Reward)
- 学习过程 : 智能体执行一个动作(Action),环境会返回一个新的**状态(State)**和一个奖励。智能体通过这种试错机制,逐步发现哪些动作在哪些状态下能带来最高的长期回报
- 核心要素 : 状态、动作、奖励、策略(Policy)和价值函数(Value Function)
- 应用: 机器人控制、自动驾驶、游戏AI(如 AlphaGo)、资源调度等
注:强化学习解决有监督学习和无监督学习无法处理的序列决策 和长期规划 问题,因为它不依赖于人类提供的"正确答案"标签,而是通过奖励反馈自主学习
31.2 Example (Mars Rover)
以一个简化版的火星探测器模型作为例子,介绍强化学习
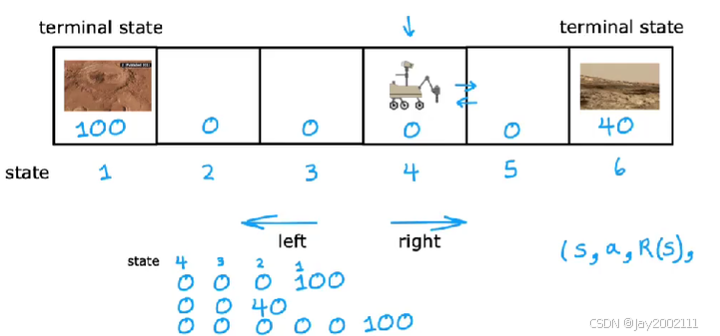
如上图,简化为6个状态,且只能向左或向右移动,最左和最右为终端状态(Terminal State),标志着一个训练或运行回合的终点,最左边奖励为100,最右边奖励为40,中间都为0
31.3 The Return in Reinforcement Learning
如果执行一次动作,即向左或向右走,这个行动的代价为0的话,那么显然一直向左走比较好,因为左边的终端状态奖励更大。但是在实际任务中往往不是这样,而是要考虑行动的成本
我们用回报(Return)来表示从某个时间步开始,到本回合结束,智能体能够获得的所有未来奖励的累积总和 。用 折扣因子(Discount Factor) 是衡量未来奖励相对于即时奖励的价值,当前状态的奖励乘折扣因子的0次方,下一个状态乘1次方,再下一个乘2次方,以此类推
以探测器为例,假设折扣因子设为0.9,初始在状态4,一直向左走的回报即为:Return=0+(0.9)×0+(0.9)2×0+(0.9)3×100=72.9Return = 0 + (0.9) \times 0 + (0.9)^2 \times 0 + (0.9)^3 \times 100 = 72.9Return=0+(0.9)×0+(0.9)2×0+(0.9)3×100=72.9
注:
- 折扣因子通常用γ\gammaγ表示
- 折扣因子通常取0.9,0.99,0.999这类数字,但是后续的例子中为了在较少的步骤中体现出折扣因子的作用,设为0.5
- 如果存在负奖励,那么折扣因子的出现,最优策略会将负奖励尽量推迟
31.4 Policies in Reinforcement Learning
策略(Policy,π\piπ)是智能体在特定状态下,选择动作的规则或函数。即π(s)=a\pi (s) = aπ(s)=a,输入state,输出action
31.5 Review of Key Concepts
前面介绍的强化学习的流程,实际上是马尔科夫决策过程(Markov Decision Process,MDP)
关键在于其马尔科夫性:未来只取决于当前状态和动作,与过去的历史无关 。这使得我们只需要关注当前状态就能进行决策,极大地简化了问题
32 State-action Value Function
32.1 State-action Value Function Definition
为了找到最优策略,我们需要评估一个策略的好坏。在实际决策时,我们更需要知道在某个特定状态下,采取某个特定动作后,能获得多少期望回报。
我们引入状态-动作值函数(State-action Value Function) ,又称Q函数(Q-Function) :Q(s,a)Q(s, a)Q(s,a)
Q函数的值等于,在某个状态s后只采取一次动作a,并且之后都采用最优策略所得到的回报
这个定义中出现了"最优策略"可能有些奇怪,但是后续的介绍会说明。总之,计算出了Q函数的值,我们就能知道当前状态应该采取什么策略最优
注:在某些文献中,用Q∗Q^{*}Q∗表示Q函数
32.2 Bellman Equation 贝尔曼方程
贝尔曼方程可以用来帮助计算Q函数
记s为当前状态,a为当前采取的动作,s'为采取动作a后到达的状态,a'为状态s'下采取的动作,R(s)表示当前状态s的奖励,那么贝尔曼方程为:
Q(s,a)=R(s)+γmaxa′Q(s′,a′)Q(s, a) = R(s) + \gamma \max_{a'} Q(s', a')Q(s,a)=R(s)+γa′maxQ(s′,a′)
这非常符合直觉,当前价值 Q(s,a)Q(s, a)Q(s,a) = 立即回报 R(s)R(s)R(s) + 对未来的期望 γmaxa′Q(s′,a′)\gamma \max_{a'} Q(s', a')γmaxa′Q(s′,a′)。因为当前这一步比下一步多一步,所以后一项要乘以折扣因子γ\gammaγ
32.3 Stochastic Environment 随机环境
有时,我们根据策略采取动作a,但是实际上会因为一些意外情况,并不会实际执行a,例如,发指令给火星探测车向左走,但可能因为滑坡导致有一定概率向右走了
随机环境指的是在给定当前状态s并采取动作a后,环境不是确定性地转移到下一个状态s',而是以一定的概率转移到多个可能的状态s1′,s2′,...s_1', s_2', \dotss1′,s2′,...
此时,我们考虑最优策略,是最大化汇报的期望,那么贝尔曼方程改为:
Q(s,a)=R(s)+γE(maxa′Q(s′,a′))Q(s, a) = R(s) + \gamma E(\max_{a'} Q(s', a'))Q(s,a)=R(s)+γE(a′maxQ(s′,a′))