基于粒子群算法的 33 节点配电网重构 MATLAB 程序探索

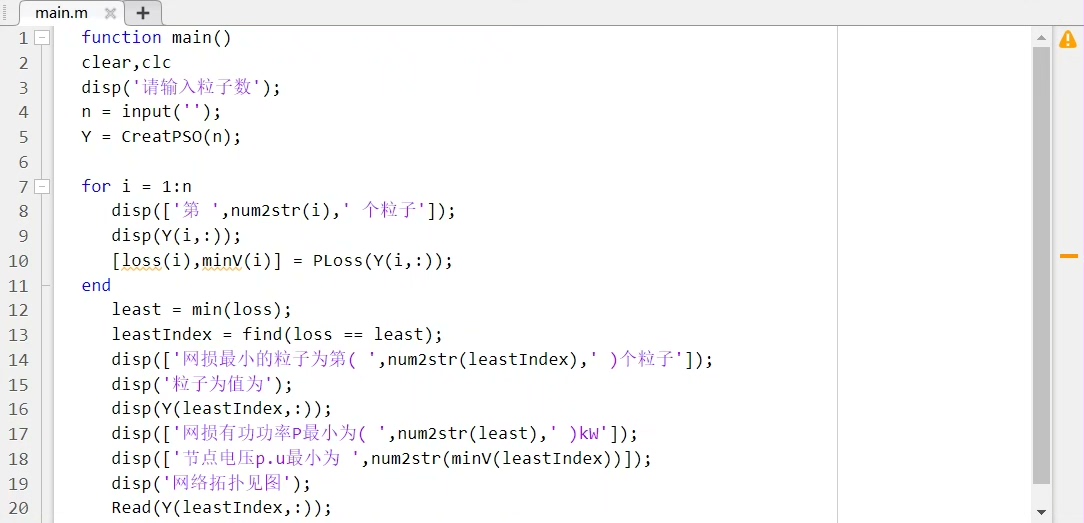
基于粒子群算法的配电网重构 MATLAB程序 33节点

在电力系统领域，配电网重构是一项重要任务，旨在通过改变配电网中开关的状态，优化网络结构，降低网损、提高供电可靠性等。粒子群算法（PSO）因其高效、易实现等特点，常被用于解决这类复杂的优化问题。今天咱就来唠唠基于粒子群算法的 33 节点配电网重构的 MATLAB 程序。

粒子群算法基本原理

粒子群算法模拟鸟群觅食行为。想象一群鸟在一个空间里找食物，每只鸟（粒子）都知道自己当前位置和到目前为止找到的最优位置（个体极值 pbest），同时也知道整个鸟群找到的最优位置（全局极值 gbest）。粒子通过不断调整自己的速度和位置，向着更好的解飞行。

在数学上，粒子 i 在第 d 维的速度更新公式为：

\[ v*{id}(t + 1) = w \cdot v* {id}(t) + c1r {1id}(t) (p*{id}(t) - x* {id}(t)) + c2r {2id}(t) (g*{d}(t) - x*{id}(t)) \]

其中，\( w \) 是惯性权重，影响粒子对自身历史速度的继承程度；\( c1 \) 和 \( c 2 \) 是学习因子，控制粒子向个体极值和全局极值飞行的步长；\( r*{1id} \) 和 \( r*{2id} \) 是介于 0 到 1 之间的随机数。粒子位置更新公式为：

\[ x*{id}(t + 1) = x*{id}(t) + v_{id}(t + 1) \]

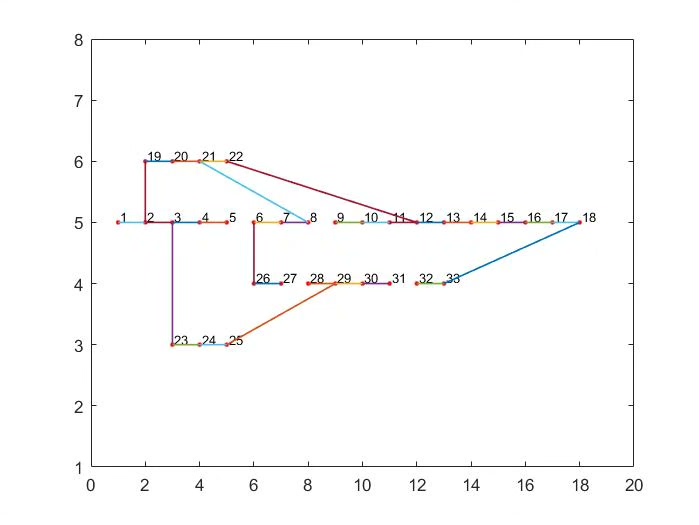
33 节点配电网模型

33 节点配电网是一个经典的测试系统，它有特定的拓扑结构和参数。在 MATLAB 中，我们可以通过矩阵来描述其网络结构，比如用一个支路矩阵来记录每条支路的起点、终点、电阻、电抗等信息。

matlab 复制代码

% 33节点配电网支路数据
branch = [1 2 0.0922 0.0470;
          2 3 0.4930 0.2511;
          3 4 0.3660 0.1864;
          % 省略其他支路数据
         ];

上面这段代码简单定义了部分 33 节点配电网的支路数据，每行分别代表一条支路的起点、终点、电阻和电抗。

基于粒子群算法的配电网重构 MATLAB 实现

matlab 复制代码

% 参数设置
npop = 50; % 粒子数量
maxgen = 100; % 最大迭代次数
w = 0.7; % 惯性权重
c1 = 1.5; % 学习因子1
c2 = 1.5; % 学习因子2

% 初始化粒子位置和速度
pos = zeros(npop, size(branch, 1));
vel = zeros(npop, size(branch, 1));
for i = 1:npop
    pos(i, :) = randi([0 1], 1, size(branch, 1)); % 随机初始化开关状态（0或1）
    vel(i, :) = randn(1, size(branch, 1));
end

% 初始化个体极值和全局极值
pbest = pos;
pbest_fitness = Inf(npop, 1);
gbest = pos(1, :);
gbest_fitness = Inf;

for gen = 1:maxgen
    for i = 1:npop
        % 计算适应度（这里以网损为例）
        fitness = calculate_loss(pos(i, :), branch);
        if fitness < pbest_fitness(i)
            pbest_fitness(i) = fitness;
            pbest(i, :) = pos(i, :);
        end
        if fitness < gbest_fitness
            gbest_fitness = fitness;
            gbest = pos(i, :);
        end
    end
    % 更新速度和位置
    for i = 1:npop
        vel(i, :) = w * vel(i, :) + c1 * rand(1, size(branch, 1)).*(pbest(i, :) - pos(i, :)) + c2 * rand(1, size(branch, 1)).*(gbest - pos(i, :));
        pos(i, :) = pos(i, :) + vel(i, :);
        % 限制位置在0和1之间
        pos(i, pos(i, :) > 1) = 1;
        pos(i, pos(i, :) < 0) = 0;
    end
end

代码分析

参数设置 ：定义了粒子群算法所需的关键参数，像粒子数量 npop、最大迭代次数 maxgen 以及惯性权重 w 和学习因子 c1、c2。这些参数对算法的收敛速度和寻优效果有很大影响。比如 w 较大时，粒子更倾向于保持之前的搜索方向，全局搜索能力强；较小时，粒子更关注局部区域，利于精细搜索。
初始化粒子 ：随机生成粒子的初始位置 pos，这里用 0 和 1 表示开关状态，1 表示闭合，0 表示断开。速度 vel 也随机初始化。
个体极值和全局极值初始化 ：将每个粒子的初始位置设为个体极值 pbest，适应度设为无穷大 Inf。全局极值 gbest 初始化为第一个粒子的位置，全局适应度也设为无穷大。
迭代寻优 ：在每次迭代中，计算每个粒子位置对应的适应度（这里以网损作为适应度函数，通过 calculate_loss 函数计算）。如果当前粒子的适应度比其个体极值好，更新个体极值；如果比全局极值好，更新全局极值。然后根据速度和位置更新公式更新粒子的速度和位置，并将位置限制在 0 到 1 之间，确保其代表合理的开关状态。

通过这样的 MATLAB 程序实现，利用粒子群算法可以有效地对 33 节点配电网进行重构，找到使网损等目标最优的开关状态组合。当然，实际应用中还可能需要考虑更多因素，如电压约束、负荷变化等，但这个基础的程序框架为进一步研究提供了很好的起点。