探索Matlab/Simulink下基于ADRC的半车主动悬架建模与控制

matlab/simulink半车主动悬架建模：基于ADRC(自抗扰控制)的主动悬架控制。主体模型为半车主动悬架，采取ADRC控制。输出为车身加速度，悬架动挠度，轮胎动变形。默认输入为正弦路面输入。有与pid控制的效果对比。

在汽车工程领域，悬架系统对于车辆行驶舒适性和安全性起着至关重要的作用。主动悬架作为一种先进的悬架技术，能够根据路面状况和车辆行驶状态实时调整悬架参数，从而显著提升车辆性能。今天咱们就来聊聊在Matlab/Simulink环境下，基于自抗扰控制（ADRC）的半车主动悬架建模与控制，顺便对比一下它和PID控制的效果。

一、半车主动悬架主体模型搭建

半车模型是在研究悬架系统时常用的一种简化模型，它考虑了车身垂直运动、俯仰运动以及两个车轴的垂直运动，能较好地反映车辆悬架系统的动态特性。在Simulink中搭建这个模型，我们需要定义各个部件的参数，像车身质量、悬架刚度、阻尼系数等等。

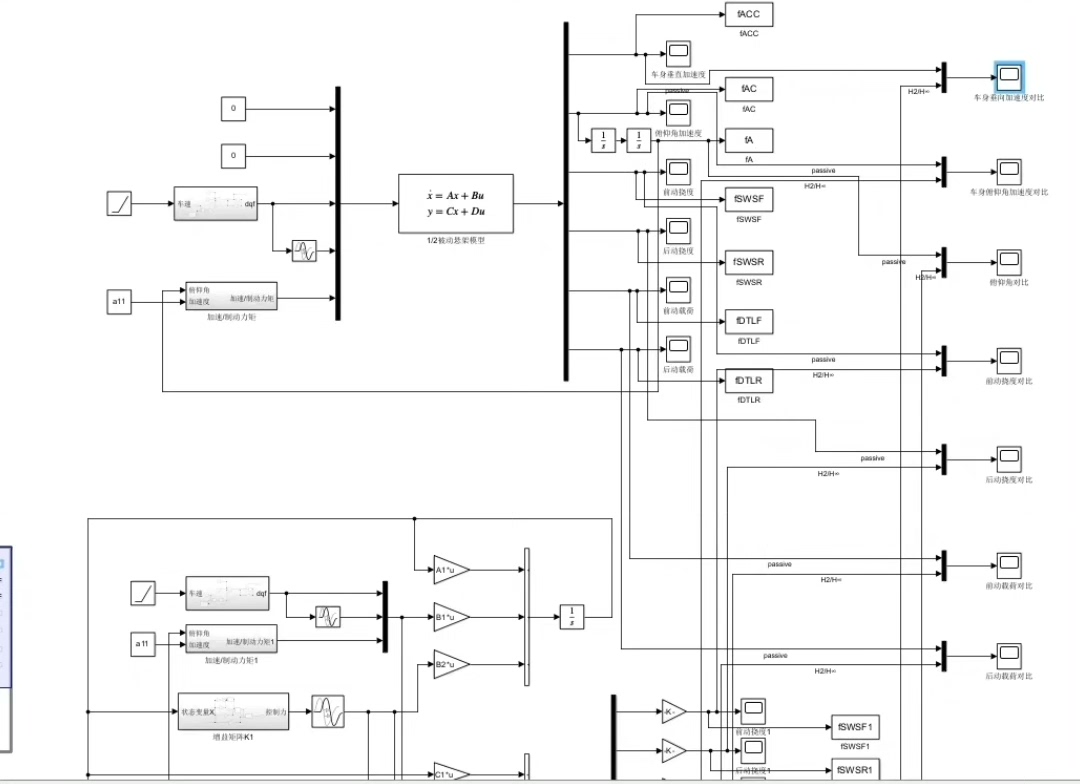
比如，以下是一段简单的Matlab代码用于定义部分模型参数：

matlab 复制代码

% 定义车身质量
m_s = 1000; % 单位：kg
% 定义悬架刚度
k_s = 20000; % 单位：N/m
% 定义悬架阻尼系数
c_s = 1000; % 单位：N·s/m

这些参数的设置会直接影响到悬架系统的性能表现，在实际建模过程中，需要根据具体车型和研究目的进行调整优化。

二、ADRC控制策略实现

自抗扰控制（ADRC）是一种不依赖精确数学模型的新型控制策略，它具有较强的抗干扰能力和自适应能力。在主动悬架控制中应用ADRC，可以有效地抑制路面不平度等干扰对车辆行驶性能的影响。

在Simulink里实现ADRC控制，首先要搭建扩张状态观测器（ESO）来估计系统的状态和干扰。以下是一个简单的ESO结构代码示意（以离散形式为例）：

matlab 复制代码

% 假设系统状态 x1,x2
% 离散时间步长 dt
dt = 0.01;
% 观测器增益
beta01 = 100;
beta02 = 1000;
% 初始化观测状态
z1 = 0;
z2 = 0;
% 系统输入 u 和输出 y
u = 0;
y = 0;
for k = 1:1000
    e = y - z1;
    z1 = z1 + dt * (z2 - beta01 * e);
    z2 = z2 + dt * (-beta02 * e);
    % 根据估计状态计算控制量等后续操作
end

这段代码简单展示了ESO如何根据系统输出和输入，通过不断迭代来估计系统状态。这里的beta01和beta02是观测器增益，它们的取值会影响观测器的收敛速度和估计精度，需要通过调试优化来确定合适的值。

然后，基于ESO的估计结果，设计非线性状态误差反馈控制律（NLSEF）来计算控制输入。例如：

matlab 复制代码

% 控制律增益
k_p = 10;
k_d = 2;
% 参考输入 r
r = 0;
for k = 1:1000
    % 状态误差
    e1 = r - z1;
    e2 = 0 - z2;
    % 控制量
    u0 = k_p * e1 + k_d * e2;
    % 补偿干扰估计值
    u = u0 - z2;
end

这里kp**和k d是控制律增益，决定了控制器对状态误差的响应程度。最终计算得到的u就是施加到主动悬架系统的控制输入。

三、输入设定与输出指标

咱们默认输入为正弦路面输入，这可以通过Simulink中的信号发生器模块轻松实现。设置合适的幅值和频率，来模拟不同路况。比如设置幅值为0.05m，频率为1Hz，就大概模拟了一种中等颠簸程度的路面。

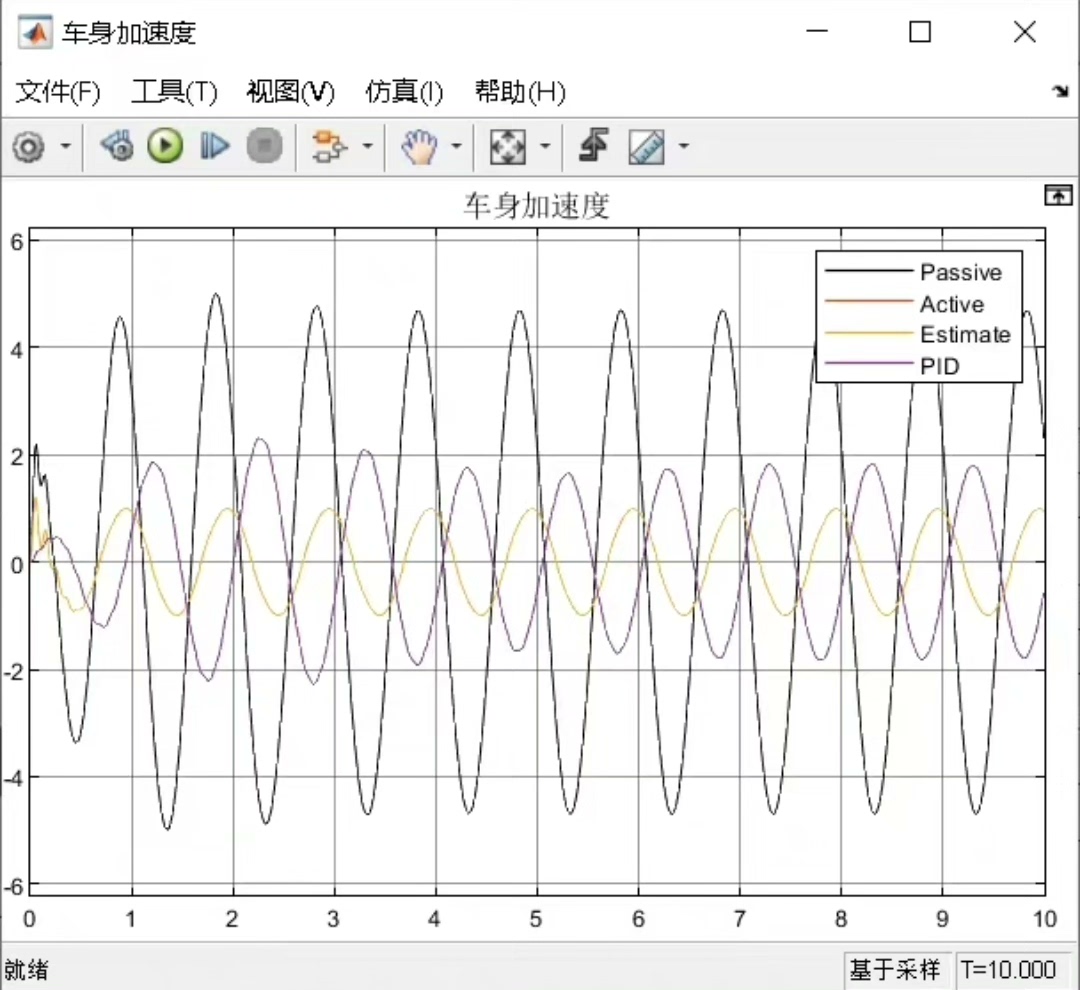
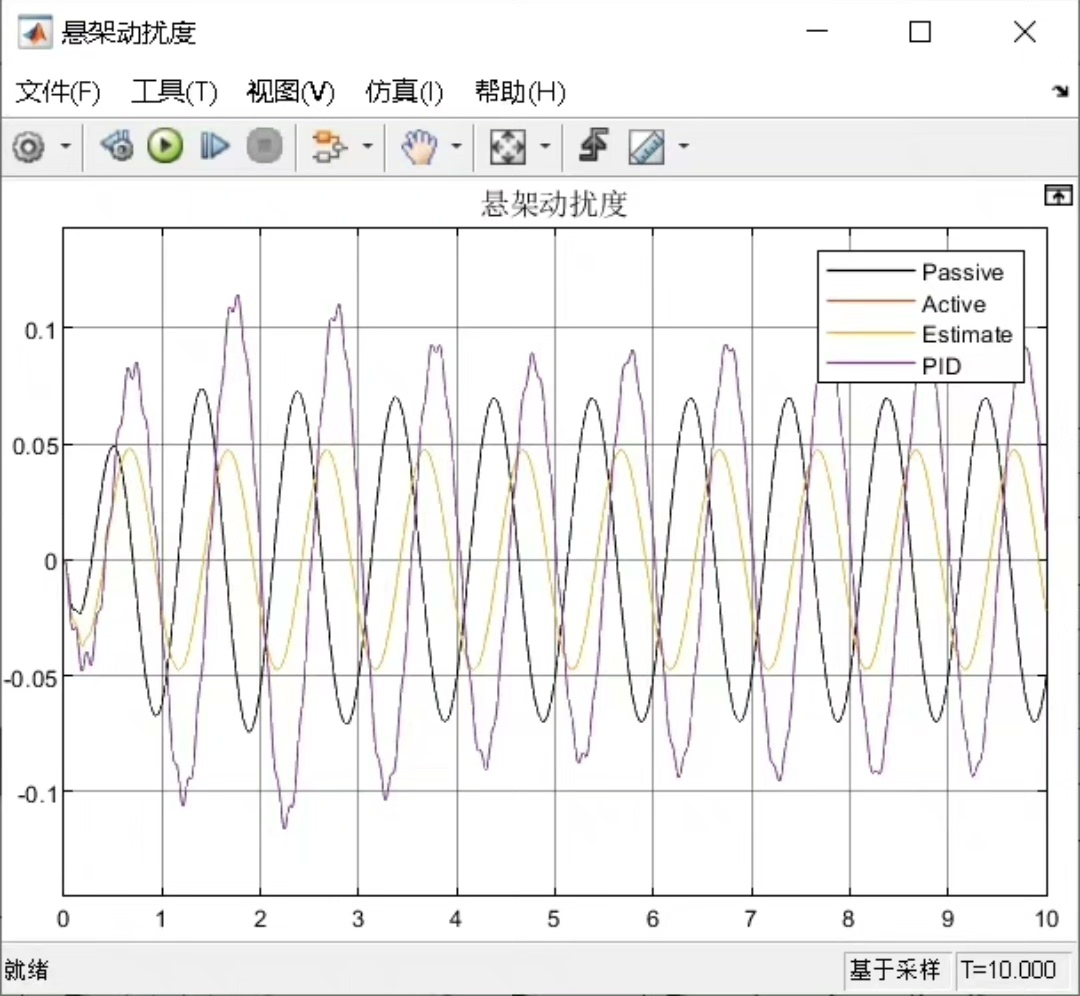
模型的输出主要关注车身加速度、悬架动挠度和轮胎动变形这几个指标。车身加速度直接关系到乘坐舒适性，悬架动挠度反映了悬架的工作范围，轮胎动变形则与轮胎接地性和行驶安全性相关。在Simulink模型中，我们可以通过添加相应的传感器模块来获取这些输出信号，并利用示波器等工具进行实时观测和分析。

四、与PID控制效果对比

PID控制是一种经典且广泛应用的控制策略。为了对比ADRC和PID控制在半车主动悬架系统中的效果，我们在同样的模型和输入条件下搭建PID控制器。

PID控制的核心代码如下：

matlab 复制代码

% PID参数
Kp = 5;
Ki = 0.1;
Kd = 1;
% 积分项
integral = 0;
% 上一时刻误差
prev_error = 0;
for k = 1:1000
    % 参考输入 r 和实际输出 y
    r = 0;
    y = 0;
    error = r - y;
    integral = integral + error * dt;
    derivative = (error - prev_error) / dt;
    u = Kp * error + Ki * integral + Kd * derivative;
    prev_error = error;
end

这里Kp、Ki和Kd分别是比例、积分和微分系数，它们的取值需要反复调试来达到较好的控制效果。

从实际对比结果来看，在正弦路面输入下，ADRC控制的车身加速度波动更小，能更好地维持车辆的平稳行驶，乘坐舒适性明显提升；在悬架动挠度方面，ADRC也能将其控制在更合理的范围内，减少悬架过度压缩或拉伸的情况；对于轮胎动变形，ADRC同样展现出了比PID控制更好的抑制能力，保障了轮胎与地面的良好接触。

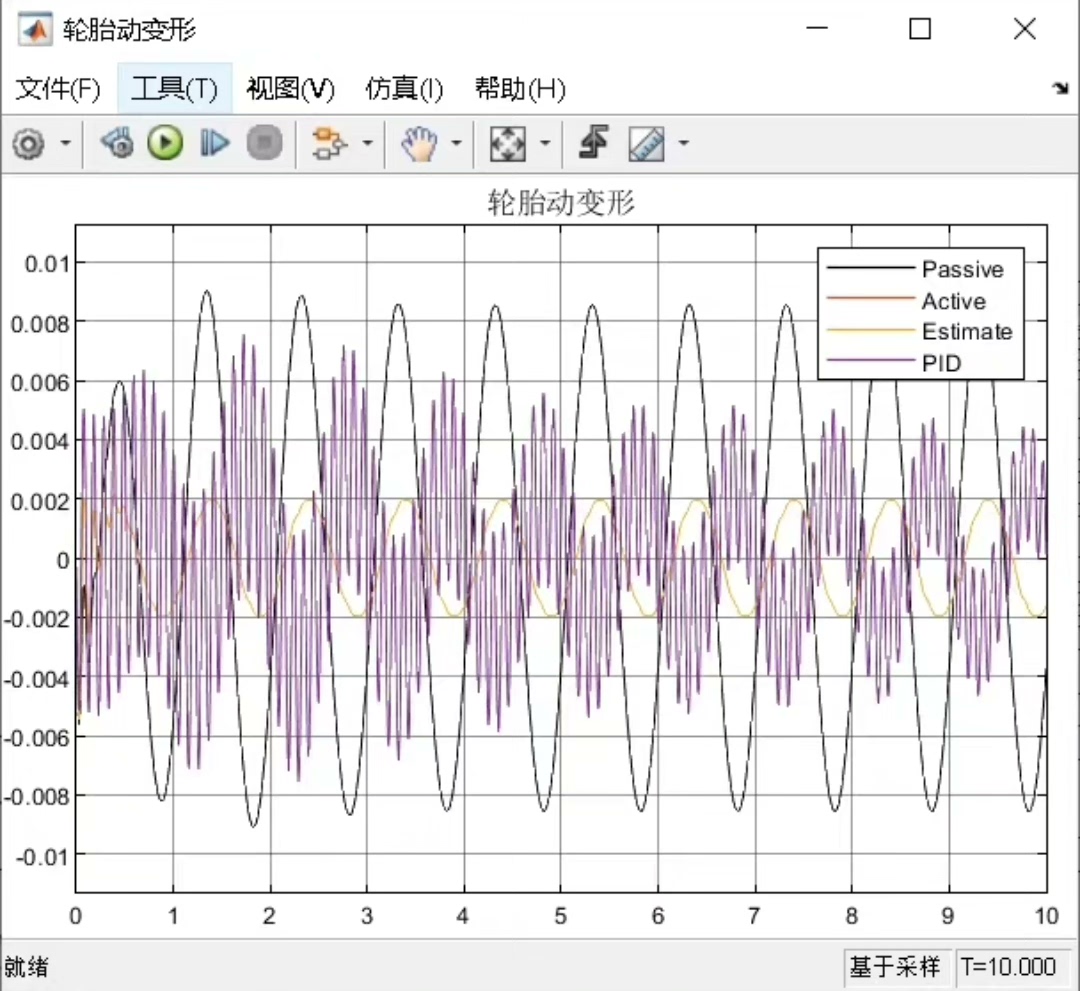
总的来说，基于ADRC的半车主动悬架控制在Matlab/Simulink环境下展现出了优秀的性能，相比传统PID控制在车辆行驶舒适性和安全性方面有显著优势。当然，实际应用中还需要考虑更多复杂因素，但这个研究为主动悬架控制技术的发展提供了有价值的参考。希望这篇博文能让大家对基于ADRC的半车主动悬架建模与控制有更深入的理解，欢迎一起探讨交流。