今天继续进行机器学习算法的学习,在上一篇博客中我们介绍了knn算法和线性回归。逻辑回归其实是在线性回归的基础上演变出来的。
逻辑回归的作用:
实现二分类。
原理拆解:
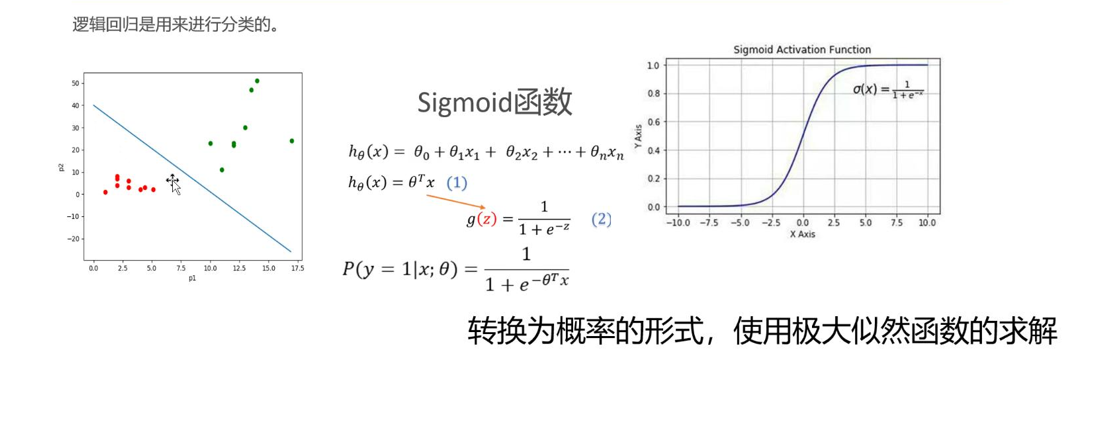
本质:
为什么说逻辑回归还是线性模型,因为逻辑回归本质上就是通过找到一条线把数据分成两类。如图,我们用一条线分隔红色和绿色的数据集。
求解直线:
我们通过极大似然函数来求解直线方程。
思路和我们上一篇博客线性回归是一样的,我们通过"把所有数据集带入直线得到分类的概率的累乘取得最大值"这个关系来求解方程系数。
具体操作:
容易知道,红色数据集带入直线方程得到负数值;绿色数据集带入方程得到正数值,即我们可以通过数据集带入方程得到结果的正负实现分类。我们先介绍一个函数:sigmoid,如上图所示,这个函数把实数集投射到0到1之间,并且有如图所示特征。那么我们把数据集带入直线方程的结果带入sigmoid函数就能实现:当结果小于0.5为红色类,当结果大于0.5为绿色类。我们可以找到这样一条直线,这条直线的参数(回归系数)使得:红色类带入方程结果趋向0,绿色类结果趋向1。
于是,我们可以把直线方程带入sigmoid函数得到的函数h(x)看作每个数据取得相应分类的概率:
这里我们有一个处理,根据sigmoid函数的特点,红色数据集带入我们构造的函数h(x),结果会趋向0,我们可以把1-h(x)看作为分类的概率。如图整合,我们就得到了任意数据点属于相应分类的概率,把所有数据点取得相应分类的概率累乘,我们所需要求解的直线应该使得这个概率最大。
即: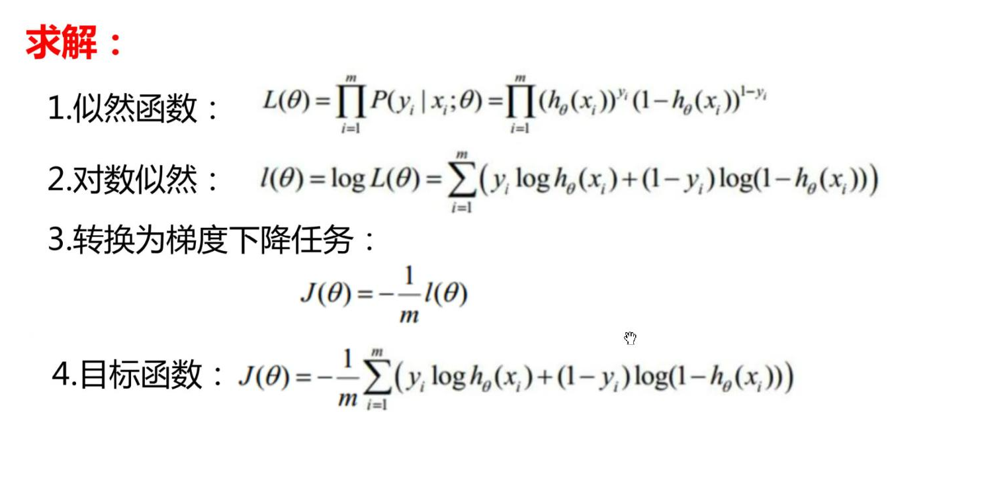
我们把求解似然函数的最大值转化为最终目标函数的最小值,这样我们就可以使用梯度下降的方法来求函数最值:
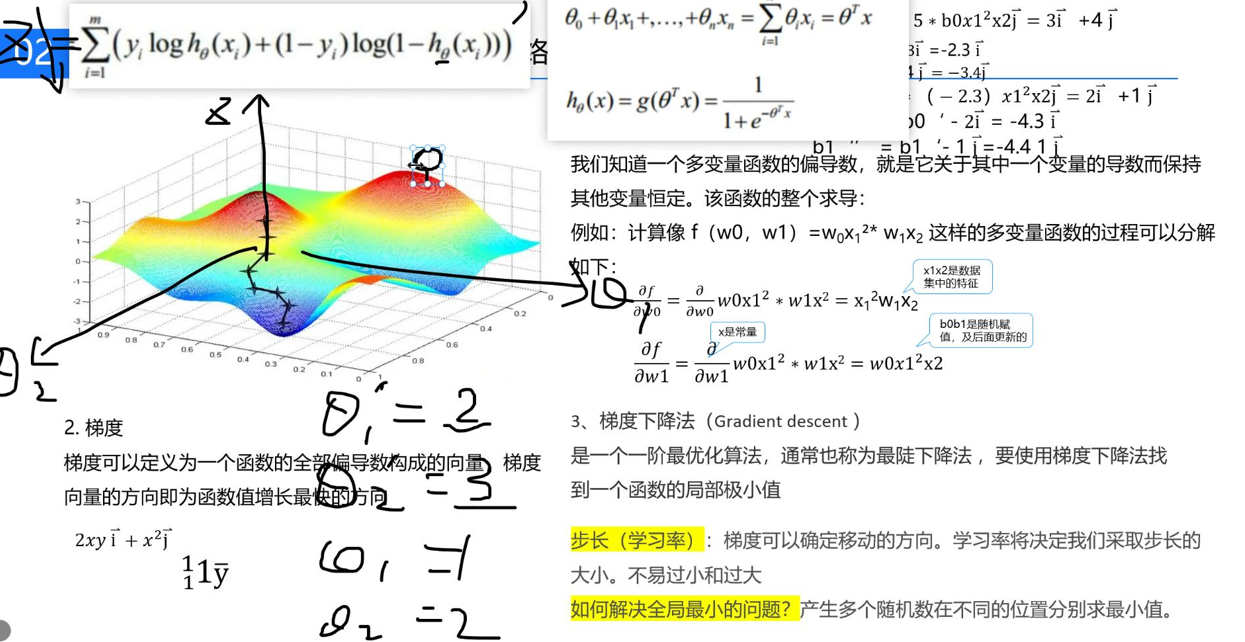
梯度下降法:假设我们在图中彩色区域(看作一片大山),我们如何到达山脚呢?到达山脚的方法,也就是求的整个函数的最小值。
我们采取这样的方法下山:我们现在位于山上某个位置,观察坡度最陡峭的方向,朝这个方向前进一个固定距离,再次重新观察最陡峭的方向,前进相同距离,以此类推。
把这样的步骤转化为数学求解函数最小值就是我们的梯度下降法:从函数上某一点开始,沿着方向导数的方向(变化率最大),前进一个步长,循环往复,从而得到最小值。
有人可能想到,我们随便从山上某一点出发,也可能没走到山脚,最终走到山中间的某个山沟子,确实有这样的情况,所以我们可以采取多个起始点来避免某个点出现这种情况。
这就是我们逻辑回归算法的内在原理。我们根据自己制定的步长来训练算法模型。
案例:
实现银行贷款申请判别系统:
这里是部分数据:
总表格包含三十万条数据,最后class为判定结果(0和1)。
我们先用python 画图直观看一下标签数据class:
画图代码:
python
#画图
import matplotlib.pyplot as plt
from pylab import mpl
#matplotlib不能显示中文,借助于pylab实现中文显示
mpl.rcParams['font.sans-serif']=['Microsoft YaHei']#显示中文
mpl.rcParams['axes.unicode_minus']= False
Labels_count = pd.value_counts(date['Class'])#统计data['class']中每类的个数L6print(labels_count)
plt.title("正负例样本数")
#设置标题#设置x轴标题
plt.xlabel("类别")
plt.ylabel("频数")#设置y轴标题
Labels_count.plot(kind='bar')#设置图像类型为bar
plt.show()
#显示数据极度样本不均衡运行: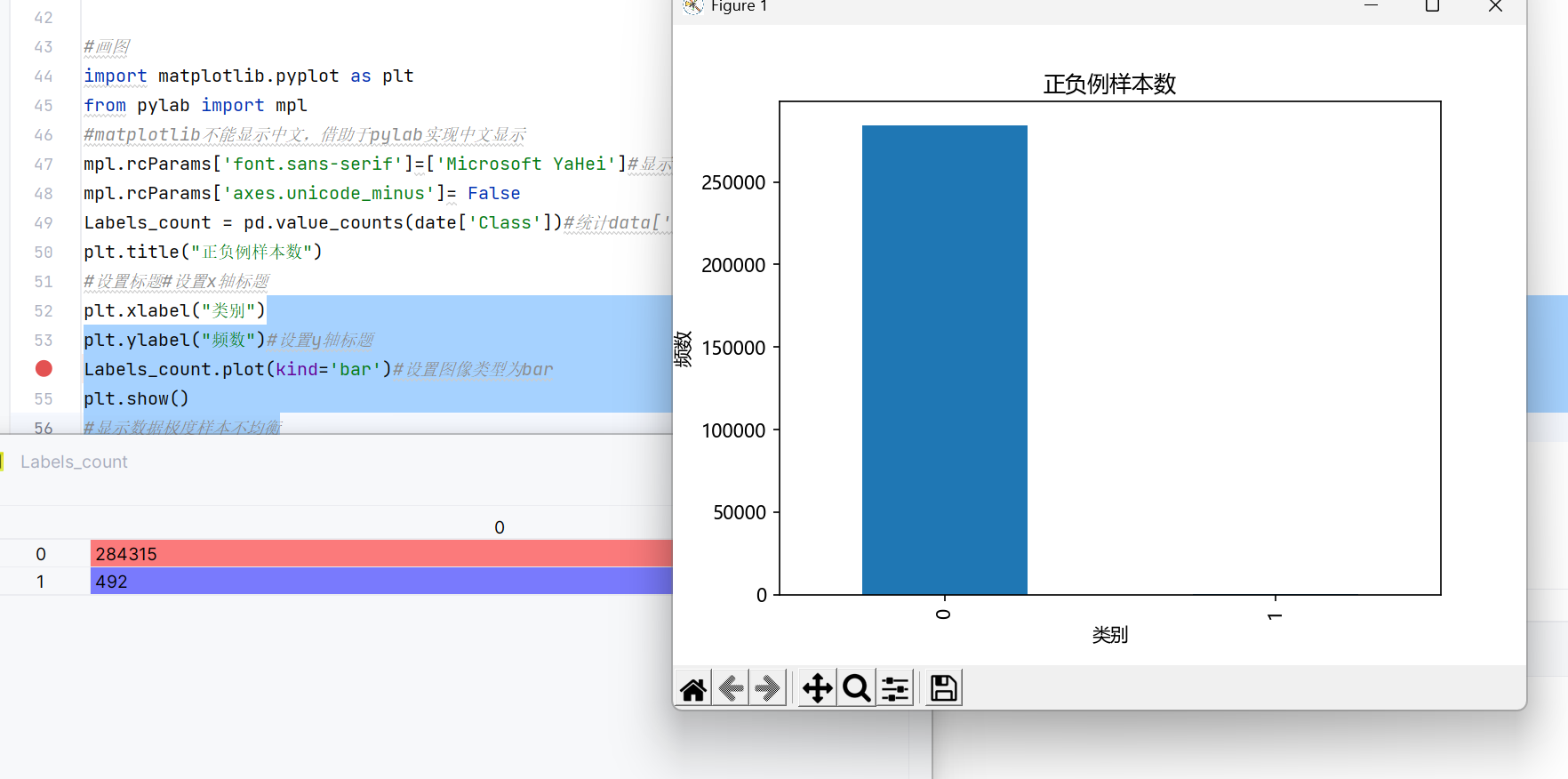
案例代码设计思路:导入相关库(逻辑回归,数据处理),对文件数据处理(读取,标准化,这里只有amount列需要标准化,删除序号列,分割成训练数据和测试数据),模型训练,模型评价。
案例代码实现:
python
import pandas as pd
from sklearn.preprocessing import StandardScaler, MinMaxScaler
date=pd.read_csv("creditcard.csv")
print(date.head()) #打印前五行数据
scaler_z = StandardScaler() #初始化类
date["Amount"]=scaler_z.fit_transform(date[["Amount"]]) #实现标准化,注意.fit_transform()方法需要二维数据,因此使用双括号
date.drop(columns="Time",inplace=True)#删除列,后面参数表示直接在原表格中删除
from sklearn.model_selection import train_test_split
X = date.drop('Class', axis=1) # 特征集(二维DataFrame)
y = date['Class'] # 标签集(一维Series)
X_train, X_test, y_train, y_test = train_test_split(
X, # 特征集
y, # 标签集
test_size=0.3, # 测试集占比(如0.2表示20%测试集,80%训练集)
random_state=42 # 随机种子(固定值可让每次切分结果一致)
)
from sklearn.linear_model import LogisticRegression
# 初始化逻辑回归模型(关键参数说明见下文)
lr = LogisticRegression(
random_state=42, # 随机种子,保证结果可复现
max_iter=1000, # 最大迭代次数(解决收敛警告)
C=1.0 # 正则化强度(C越小,正则化越强,防止过拟合)
)
# 训练模型(传入标准化后的训练集)
lr.fit(X_train, y_train)
y_pre=lr.predict(X_test)
print(lr.score(X_test,y_test))
from sklearn import metrics
print(metrics.classification_report(y_test, y_pre))运行结果: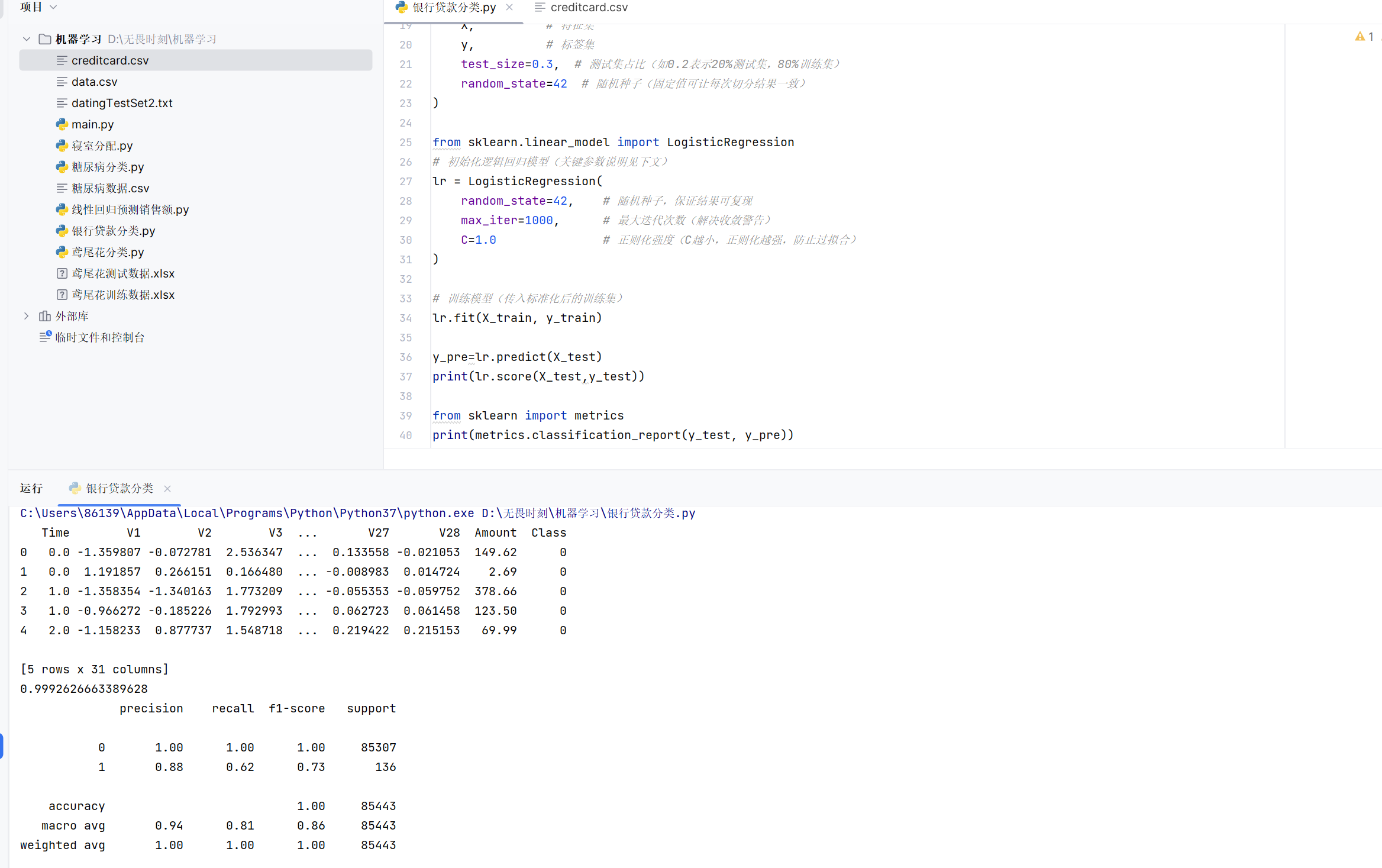
评价模块:
可以看到我们的score函数得到了0.99这样的概率,看似模型训练的很好,那么银行是不是可以使用我们的模型了呢?
答案是否定的。
我们的score得到的评价结果,完全基于准确率:预测值和真实值相同的数量占全部数据的比例。
但是我们银行最看重的是预测值的真实率,即我们预测结果为1(假设1代表是老赖),如果我们判定误判了老赖可以贷款,对银行将是巨大的损失,可以看到运行结果的recall和1对应的结果:预测值为真的概率,只有0.62,因此我们的模型对饮银行来说是完全不可行的,这个概率称为召回率。
同样我们还有精确率:真实值判定为真的概率。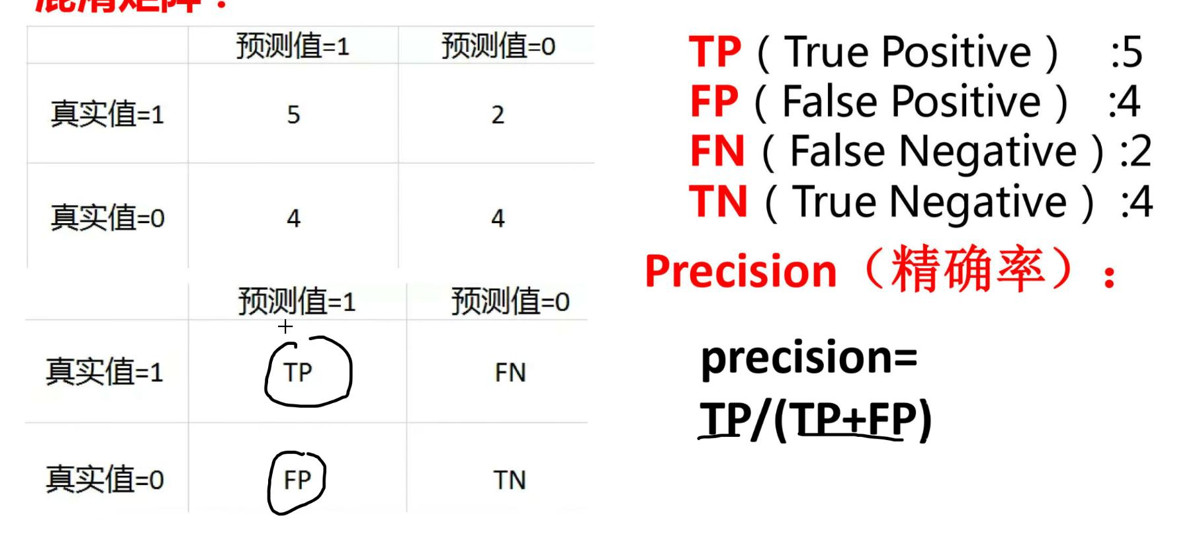
召回率:即tp/(tp+fn)
补充
过拟合,欠拟合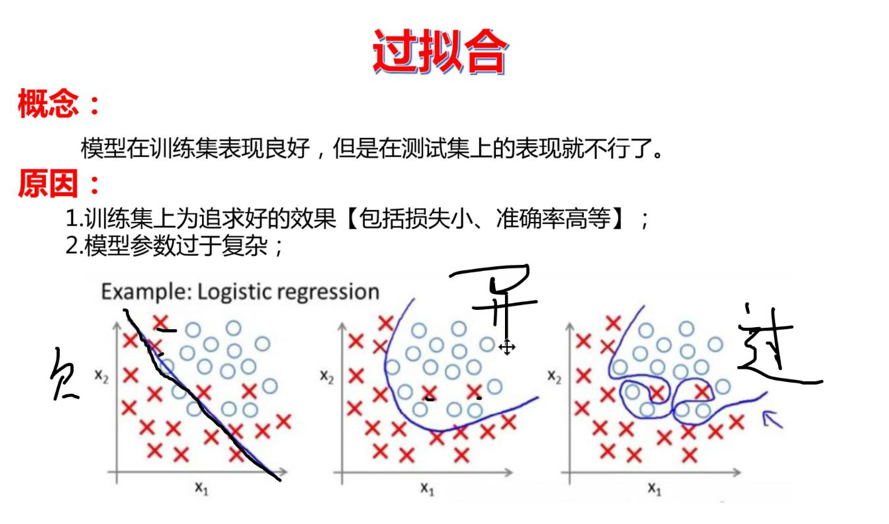
如图,模型训练的不够为欠拟合,训练过头了为过拟合(参数很复杂),我们最好的模型应该是中间这张图,因为这两个叉叉应该是异常数据。
欠拟合:训练不够,理解为,我们下山走的步长次数不够。
过拟合:训练次数过多,即步长稍大,我们走的次数又很多,于是在山脚来回横跳。
如何防止过拟合:正则化惩罚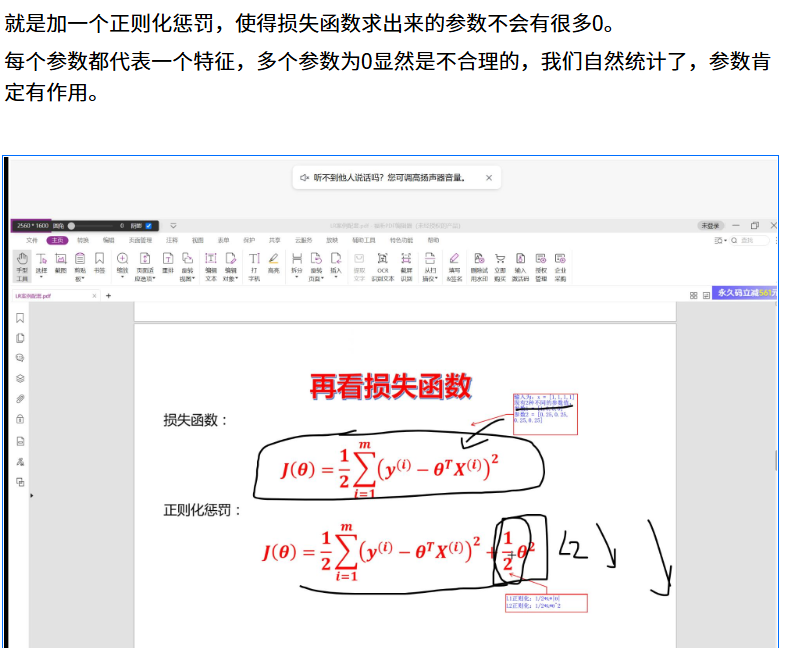
具体而言:

举例来说: