物体的多个维度
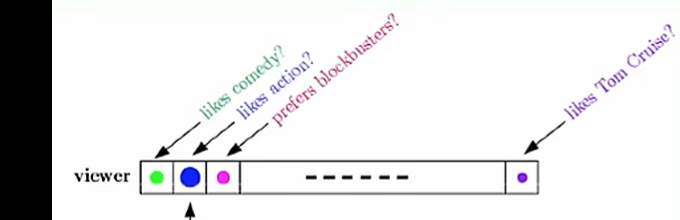
W是个多维向量,比如:苹果可以从 形状、颜色、大小、重量...方面去分析他是否是一个苹果。
W就是在这多维上的值。
公式
机器学习的分类公式如下图: f(x) = WX + b
这是一个证明某人是否能够贷款的公式,当他的分数大于threshold的时候则认为可以贷款。相当于一个二分类。
经过变换之后得到h(x),这个threshold其实就是常见的 f(x) = WX + b中的b,直线公式就是WX + b = 0

几何意义

机器学习就是在不断迭代更新W的过程,直到找到一个最适合的W
在某一t轮中,此时的W已经确定,输入X,输出Y。其中的Y是正负分类值。
定义:
g(x) 为不断迭代过程中的函数,让其趋近于真实函数;
t:迭代的轮次
以几何的形式展现出来,就是一条与W垂直的直线。
预期输出为Y=-1,在对比xg的时候,输出为y=1那么此时修正W。让WX往xg的反方向旋转,让最终的输出更加偏向于-1。于是,下一轮的W(t+1)就等于 Wt + y*X
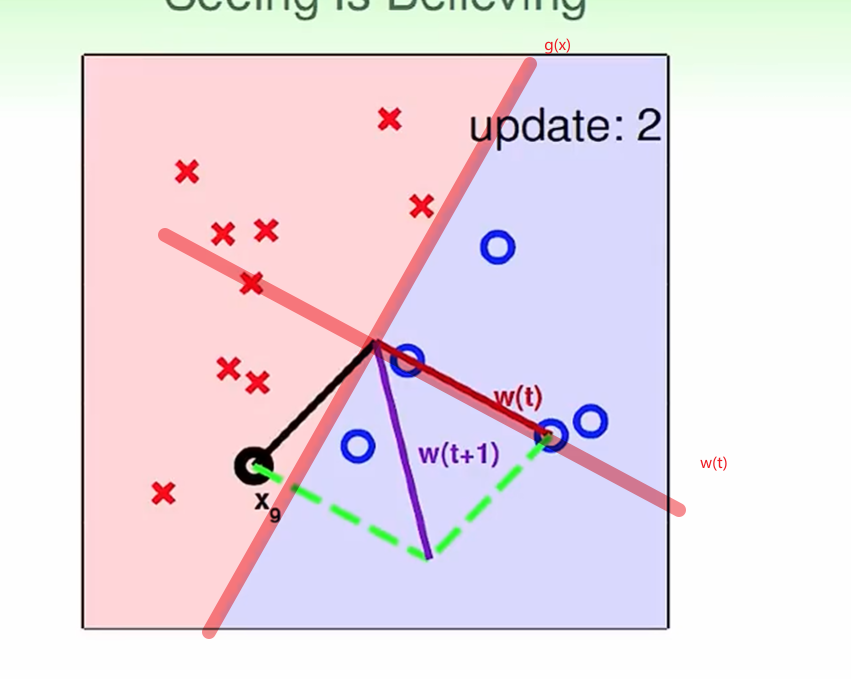
推导,以二维为例:
x + 2y + 1 = 0 --> 斜率K = - 1/2
W = (1, 2) ---> 斜率K = 2
由此可得W与分类直线在几何上垂直,推理到高纬也是如此,另外W也被叫做法向量。