用遗传算法（GA）攻克分布式置换流水车间调度问题（DPFSP）

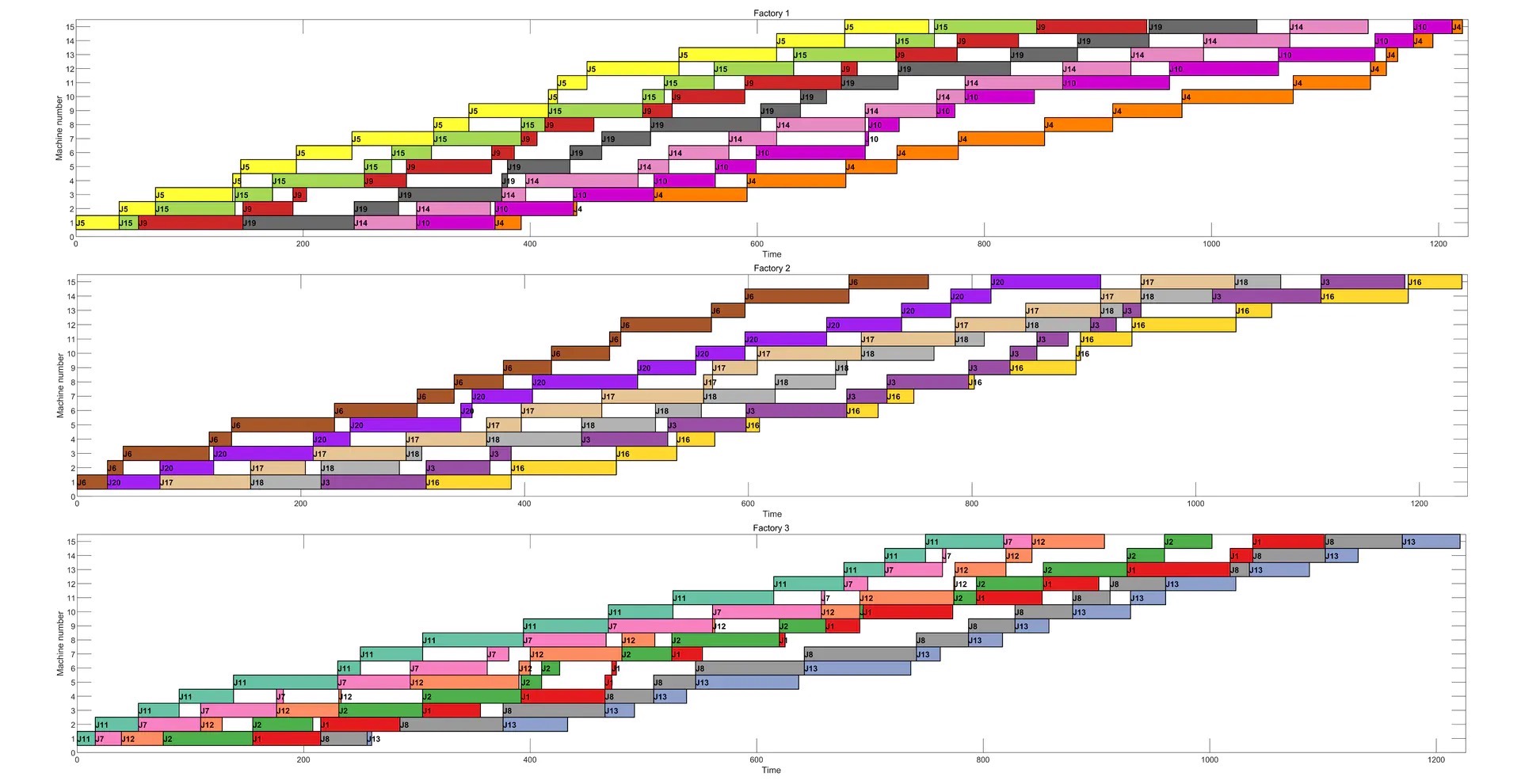
利用遗传算法(GA)求解分布式置换流水车间调度问题(Distributed permutation flow-shop scheduling problem, DPFSP) 其中：main.m是主函数运行即可；GA.m是算法的代码；color_selection用于获得甘特图的颜色配置；gantt_chart.m绘制每个工厂的甘特图；objective.m是目标函数，即计算每个工厂的Makespan并取最大值；sorting.m根据每个工厂调度方案计算每台机器任意时刻的加工信息(开始时间、结束时间、工件号、机器号), 用于绘制甘特图；调度测试集使用Rec 输出结果包括：总的Makespan、每个工厂的工件分配情况和工件排序、计算时间、最优适宜度收敛曲线、平均适宜度收敛曲线、每个工厂中的甘特图利用GA得到的20工件×15机器、3工厂的调度结果甘特图演示如下(随机运行一次的结果)：

在制造业的复杂调度场景中，分布式置换流水车间调度问题（DPFSP）一直是个颇具挑战性的任务。而遗传算法（GA）作为一种强大的优化算法，为解决此类问题提供了有效的途径。今天咱们就来唠唠如何利用GA求解DPFSP。

整体框架和关键代码文件

main.m：这就是主函数，运行它就相当于打响了这场优化战役的第一枪。就像一个总指挥，负责调用各个模块协同工作。比如：

matlab 复制代码

% main.m示例代码片段
clear all;
close all;
clc;

% 初始化参数
pop_size = 100; % 种群大小
gen = 200; % 迭代代数
% 这里省略其他参数初始化

% 调用GA算法模块
[best_sol, best_fitness, avg_fitness, time] = GA(pop_size, gen);

这段代码里，我们先清理了之前的变量，关闭所有图形窗口，然后初始化了种群大小和迭代代数，接着调用GA函数开始执行遗传算法。

GA.m：算法的核心代码就在这儿啦，它实现了遗传算法的选择、交叉、变异等一系列关键操作。以选择操作为例，假设我们采用轮盘赌选择法：

matlab 复制代码

% GA.m中轮盘赌选择法片段
function selected_pop = roulette_wheel_selection(pop, fitness)
    total_fitness = sum(fitness);
    selection_prob = fitness / total_fitness;
    selected_pop = zeros(size(pop));
    for i = 1:size(pop, 1)
        r = rand();
        sum_prob = 0;
        for j = 1:size(pop, 1)
            sum_prob = sum_prob + selection_prob(j);
            if r <= sum_prob
                selected_pop(i, :) = pop(j, :);
                break;
            end
        end
    end
end

这段代码通过计算每个个体的适应度占总适应度的比例，作为选择概率，然后通过随机数来模拟轮盘转动，选出下一代种群。

color_selection：这个模块负责获取甘特图的颜色配置，让我们的甘特图更加美观和易于区分不同任务。虽然代码可能相对简单，但作用可不小：

matlab 复制代码

% color_selection示例代码
function colors = color_selection(num_colors)
    colors = distinguishable_colors(num_colors); % 假设这里有个获取可区分颜色的函数
end

这里通过调用一个函数获取一定数量可区分的颜色，用于在甘特图中标识不同的工件或机器。

gantt_chart.m：专门绘制每个工厂的甘特图，直观展示调度结果。比如绘制甘特图的关键代码：

matlab 复制代码

% gantt_chart.m片段
figure;
hold on;
for i = 1:size(schedule, 1)
    start_time = schedule(i, 1);
    end_time = schedule(i, 2);
    job_num = schedule(i, 3);
    machine_num = schedule(i, 4);
    rectangle('Position', [start_time, machine_num, end_time - start_time, 1], 'FaceColor', colors(job_num));
end
xlabel('Time');
ylabel('Machine');
title('Gantt Chart of Factory X');
hold off;

这段代码遍历每个加工任务的信息，利用rectangle函数绘制甘特图的矩形条，展示每个任务在不同机器上的加工时间范围。

objective.m：目标函数，计算每个工厂的Makespan并取最大值。Makespan代表完成所有任务所需的总时间，是衡量调度方案优劣的重要指标。

matlab 复制代码

% objective.m代码
function makespan = objective(solutions)
    num_factories = size(solutions, 1);
    makespan_per_factory = zeros(num_factories, 1);
    for i = 1:num_factories
        % 这里省略计算每个工厂Makespan的具体逻辑
        makespan_per_factory(i) = calculate_makespan(solutions(i, :)); 
    end
    makespan = max(makespan_per_factory);
end

这段代码先遍历每个工厂的调度方案，计算各自的Makespan，然后取这些值中的最大值作为整个调度方案的Makespan。

sorting.m：根据每个工厂调度方案计算每台机器任意时刻的加工信息（开始时间、结束时间、工件号、机器号），为绘制甘特图提供数据支持。

matlab 复制代码

% sorting.m示例片段
function schedule = sorting(solution)
    % 初始化schedule矩阵
    schedule = [];
    % 遍历每个工件和机器获取加工时间信息
    for job = 1:num_jobs
        for machine = 1:num_machines
            start_time = get_start_time(solution, job, machine);
            end_time = get_end_time(solution, job, machine);
            schedule = [schedule; start_time, end_time, job, machine];
        end
    end
    % 对schedule按开始时间排序
    schedule = sortrows(schedule, 1);
end

这段代码通过遍历工件和机器，获取每个加工任务的开始和结束时间，将这些信息整理成schedule矩阵，并按开始时间排序，方便后续绘制甘特图。

调度测试集和输出结果

我们使用Rec作为调度测试集，这个测试集包含了各种复杂的调度场景，用来验证我们算法的有效性。

输出结果非常丰富：

总的Makespan ：直接反映整个调度方案的优劣，数值越小越好。通过objective.m计算得出。
每个工厂的工件分配情况和工件排序：这能让我们清晰了解每个工厂具体负责哪些工件以及加工顺序，对实际生产安排有重要指导意义。
计算时间 ：在main.m中通过记录算法开始和结束时间的差值来获取，它能帮助我们评估算法的效率。
最优适宜度收敛曲线、平均适宜度收敛曲线：可以直观展示遗传算法在迭代过程中的收敛情况，判断算法是否有效收敛到较优解。
每个工厂中的甘特图 ：由gantt_chart.m绘制，是调度结果最直观的可视化展示。就像前面提到的20工件×15机器、3工厂的调度结果甘特图，能让我们一眼看清每个工件在各个机器上的加工安排。

通过以上这些代码模块的协同工作，利用遗传算法，我们能够有效地求解分布式置换流水车间调度问题，为实际生产调度提供科学合理的方案。希望这篇博文能让大家对GA求解DPFSP有更深入的理解，一起在优化调度的道路上继续探索！