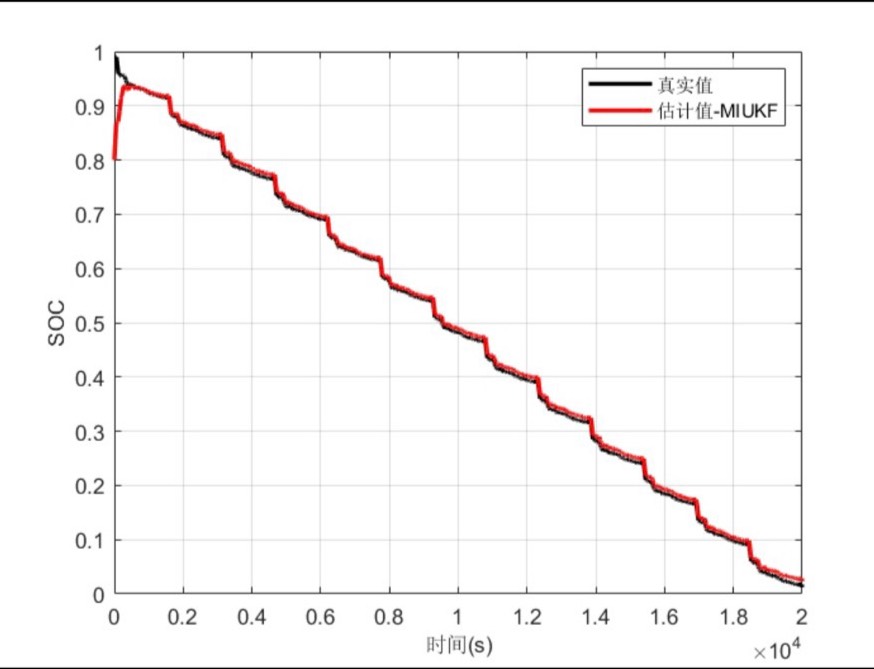
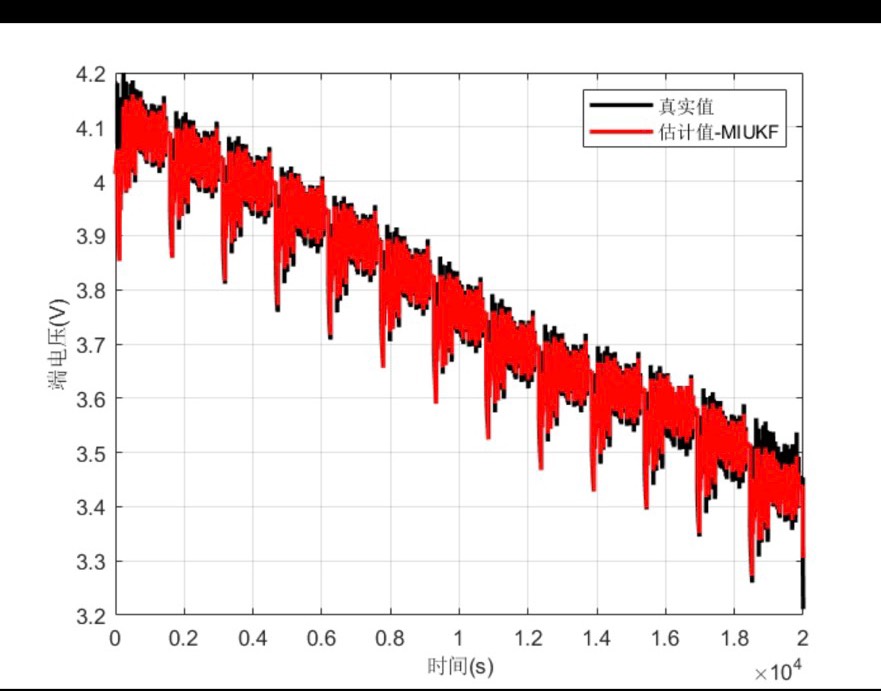
探索 MI - UKF 多新息无迹卡尔曼滤波在电池电量 SOC 估算中的应用

MI-UKF多新息无迹卡尔曼滤波电池电量SOC估算MIUKF，无迹卡尔曼滤波中加入多新息方法，文件包含有 UKF 和 EKF 的代码和仿真及对比，端电压误差等，文件中还包含 FFRLS 带遗忘因子的最小二乘法参数辨识代码和数据有参考文献，代码有注释

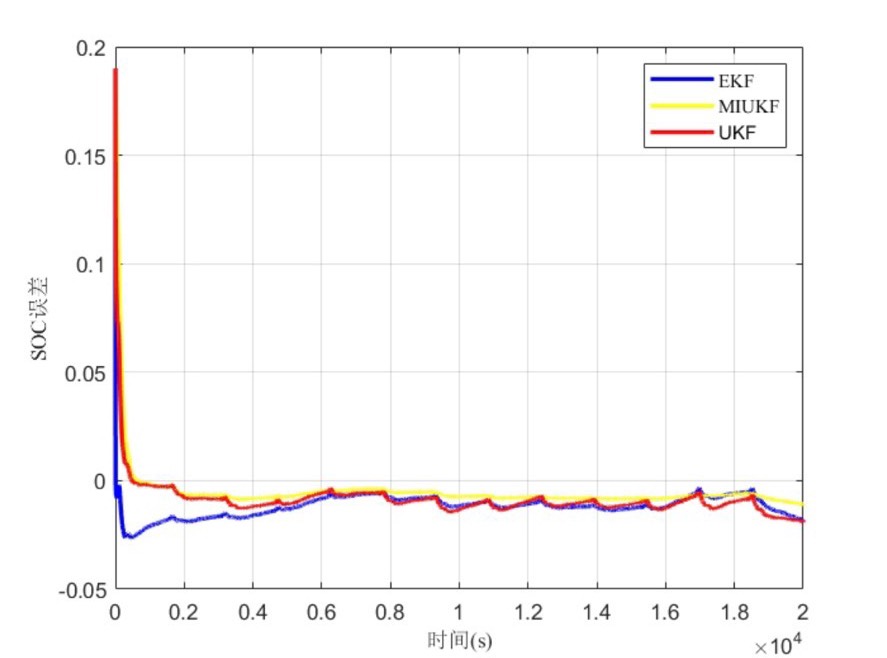
在电池管理系统中，准确估算电池电量状态（SOC）至关重要。今天咱就来唠唠 MI - UKF（多新息无迹卡尔曼滤波）在这方面的应用，这可是在无迹卡尔曼滤波基础上融入多新息方法的"秘密武器"。

一、现有代码中的宝藏：UKF 与 EKF 的对比及仿真

在提供的文件里，有 UKF 和 EKF 的代码以及它们的仿真和对比。咱们先瞧瞧 UKF 的代码片段（以下代码为示意简化版，仅为展示思路）：

python 复制代码

import numpy as np

def ukf_predict(X_hat, P, Q, f, h, R, alpha, beta, kappa):
    n = X_hat.shape[0]
    lambda_ = alpha ** 2 * (n + kappa) - n
    Wm = np.zeros(2 * n + 1)
    Wc = np.zeros(2 * n + 1)
    Wm[0] = lambda_ / (n + lambda_)
    Wc[0] = lambda_ / (n + lambda_) + (1 - alpha ** 2 + beta)
    for i in range(1, 2 * n + 1):
        Wm[i] = 1 / (2 * (n + lambda_))
        Wc[i] = 1 / (2 * (n + lambda_))

    X_sig = np.zeros((n, 2 * n + 1))
    X_sig[:, 0] = X_hat
    for i in range(1, n + 1):
        X_sig[:, i] = X_hat + np.sqrt((n + lambda_) * P)[:, i - 1]
        X_sig[:, i + n] = X_hat - np.sqrt((n + lambda_) * P)[:, i - 1]

    X_sig_p = np.zeros((n, 2 * n + 1))
    for i in range(2 * n + 1):
        X_sig_p[:, i] = f(X_sig[:, i])

    X_hat_p = np.dot(Wm, X_sig_p)
    P_p = np.zeros((n, n))
    for i in range(2 * n + 1):
        P_p += Wc[i] * np.outer(X_sig_p[:, i] - X_hat_p, X_sig_p[:, i] - X_hat_p)
    P_p += Q

    return X_hat_p, P_p

这段代码里，ukfpredict**函数实现了 UKF 的预测步骤。通过计算西格玛点、加权均值和协方差等操作，对状态进行预测。lambda 是一个关键参数，它由 ``alpha``、``kappa`` 和状态维度 ``n`` 决定，影响着西格玛点的分布。``Wm`` 和 ``Wc`` 分别是均值加权和协方差加权，为后续计算提供权重。

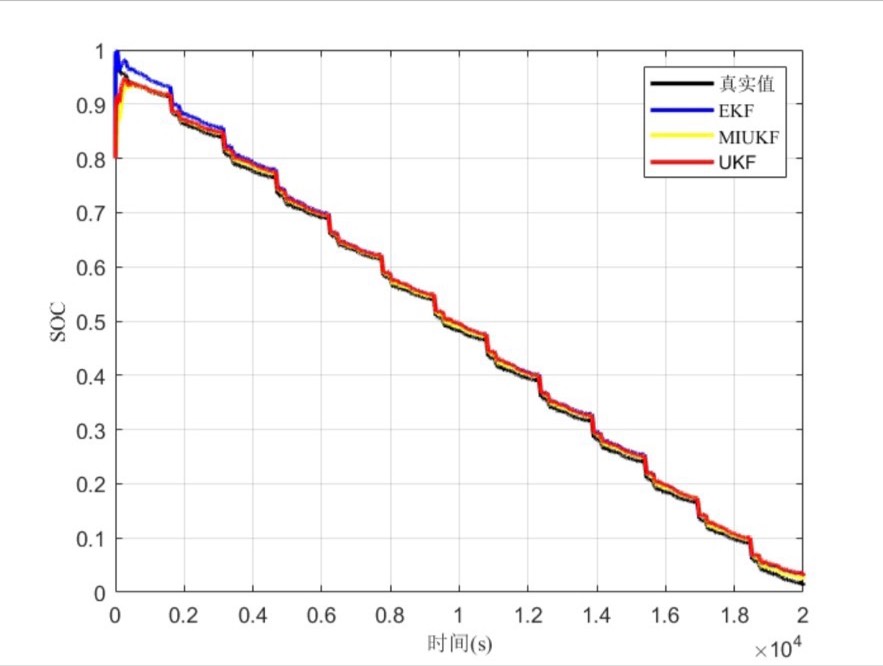
而 EKF 的代码在原理上与 UKF 不同，它基于泰勒展开线性化系统方程和观测方程。以下是 EKF 预测步骤的大致代码片段：

python 复制代码

def ekf_predict(X_hat, P, Q, F, H, R):
    X_hat = F.dot(X_hat)
    P = F.dot(P).dot(F.T) + Q
    return X_hat, P

在 EKF 里，直接利用状态转移矩阵 F 和观测矩阵 H 对状态和协方差进行更新。与 UKF 相比，EKF 计算相对简单，但线性化过程可能引入误差，在非线性较强的系统中表现可能不如 UKF。

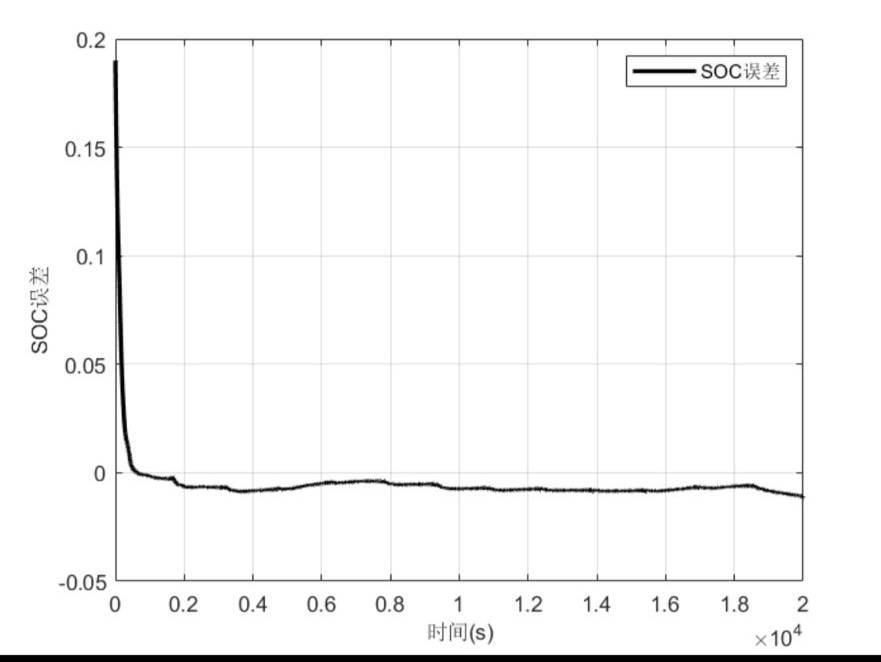
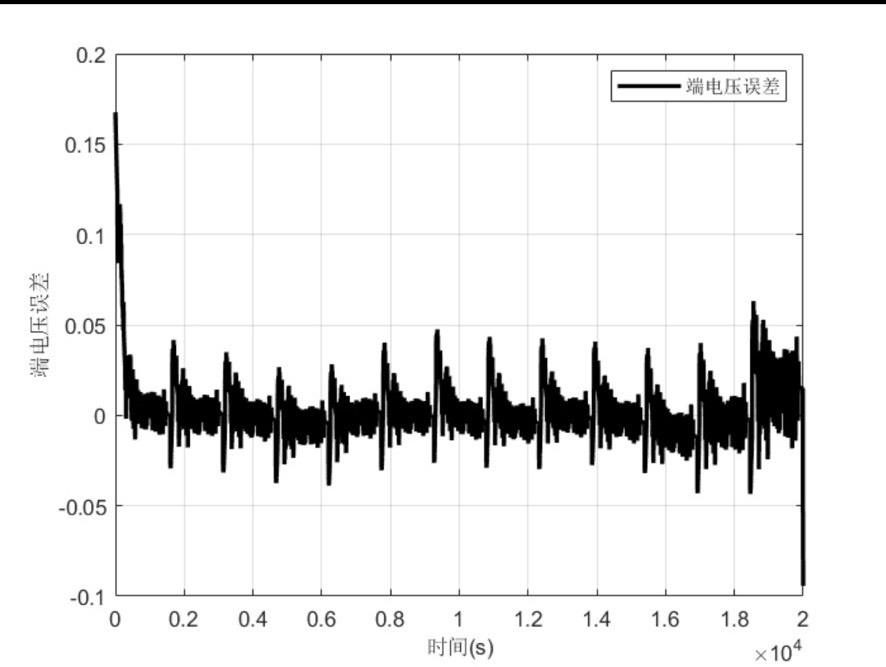
通过仿真对比两者，可以看到在估算电池 SOC 时，UKF 在处理非线性系统时往往能提供更准确的结果，特别是在端电压误差方面，UKF 展现出更好的性能。

二、FFRLS 带遗忘因子的最小二乘法参数辨识

文件里还有 FFRLS（带遗忘因子的最小二乘法）的代码和数据。这个方法在电池参数辨识中发挥着重要作用。看看下面的代码示例：

python 复制代码

import numpy as np

def ffrls(y, u, theta_hat, P, lambda_):
    phi = np.vstack((u, -y[: -1]))
    k = P.dot(phi) / (lambda_ + phi.T.dot(P).dot(phi))
    theta_hat = theta_hat + k * (y[-1] - phi.T.dot(theta_hat))
    P = (np.eye(2) - k.dot(phi.T)) / lambda_ * P
    return theta_hat, P

在这个 ffrls 函数中，y 是输出数据，u 是输入数据，thetahat**是参数估计值，P 是协方差矩阵，lambda
是遗忘因子。每次迭代时，根据新的输入输出数据，通过计算增益 ``k`` 来更新参数估计值 ``thetahat**和协方差矩阵 P。遗忘因子 lambda的作用是对旧数据进行"遗忘"，使得算法能更快适应系统参数的变化，在电池参数随时间变化的情况下，能更准确地辨识参数。

这些代码和方法相互配合，为电池电量 SOC 的准确估算提供了有力支持。结合参考文献进一步深入研究，能更好地理解这些方法背后的理论以及它们在实际应用中的优势与局限。无论是 UKF、EKF 还是 FFRLS，都在电池管理系统这个大舞台上有着独特的角色，共同推动着电池 SOC 估算技术的发展。