Lecture 2 - Image Formation
1. 2D Points
2D的点可以用常规的非齐次坐标 (inhomogeneous coordinates) 表示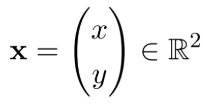
，也可以用齐次坐标 (homogeneous coordinates) 表示
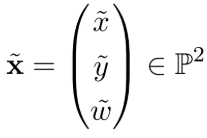，增加了一个维度
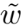，其中
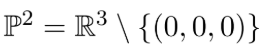(即不包括原点) 称为投影空间 。齐次坐标下坐标本身的等比例缩放不改变它所表示的点，这正是齐次的意义。
这两种表达可以相互转换。
- 非齐次 -> 齐次： 增加一个维度并设为 1 变为增广向量 (augmented vector)
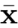，然后乘以任意的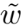进行缩放。
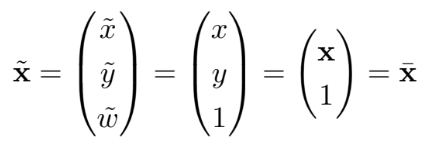
- 齐次 -> 非齐次： 上面的逆过程，除以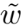使第三个维度变为1，然后去掉最后一个维度。
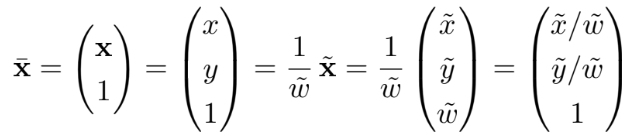
对于**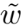 = 0** 的点称为理想点 (ideal points) 或无穷远点 (points at infinity) ，这些点不能用非齐次坐标表示。
如下图所示，增广向量的终点所在的平面 (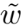= 1) 就对应了非齐次坐标平面，而齐次坐标下从原点出发的那一条射线上的所有点 (除了原点) 都代表非齐次坐标的同一个点。
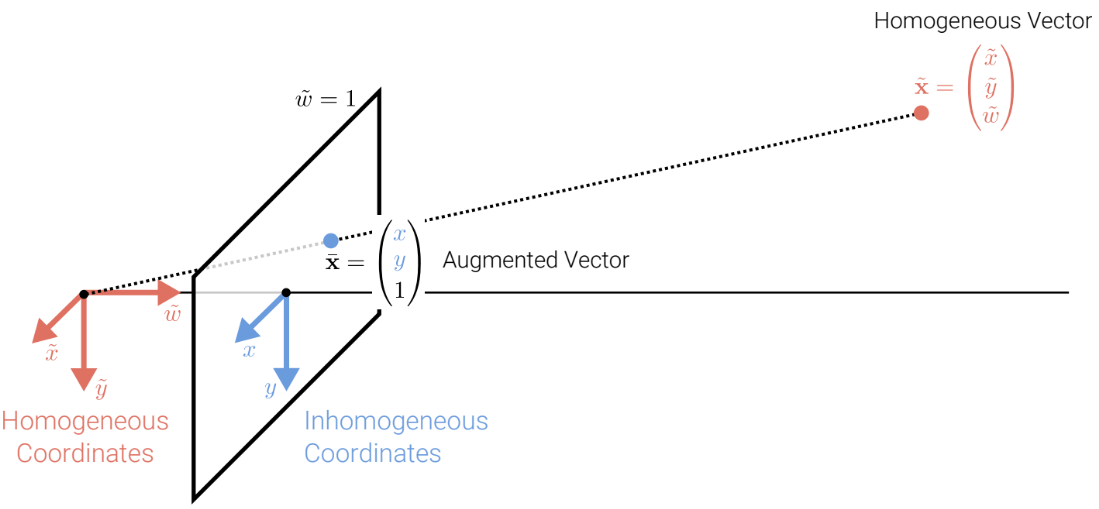
非齐次坐标与齐次坐标的映射关系
2. 2D Lines
2D的线也可以用齐次坐标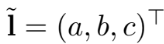
表示，其定义为
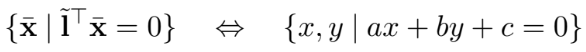，同时也满足
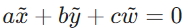. 可以对其进行缩放以规范化 (normalize) ，即令
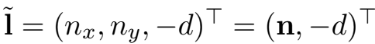，其中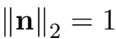
，
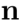是垂直于直线的法向量，
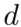是直线到原点的距离。
对于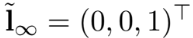
这条直线称其为无穷远线 (line at infinity) ，它穿过所有理想点。
3. Cross Product
两个向量的**叉乘 (Cross product)**可以表示为一个反对称矩阵和一个向量的乘法：
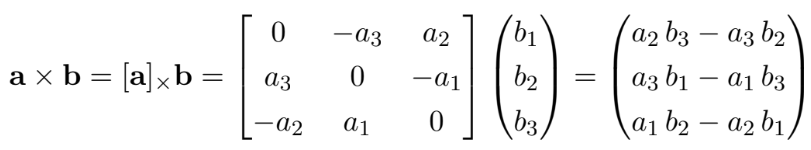
4. 2D Line Arithmetic
在齐次坐标系下，两条线的交点就是这两条线的叉乘：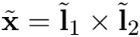
，而连接两个点的直线是这两个点的叉乘：
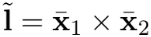. 对于证明可以从叉乘的性质 (垂直) 以及前面的定义得证。