利用PMU测量估计电力系统状态：Matlab实践与探讨

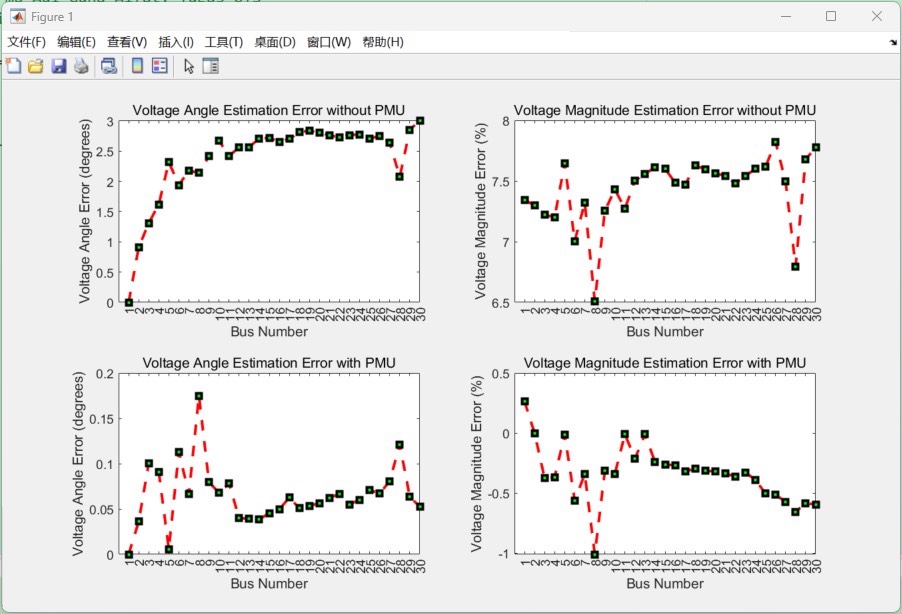
PMU测量来估计电力系统的状态。解释了使用PMU测量来估计电力系统的状态，编写了Matlab程序，并在IEEE-14总线和IEEE-30总线系统上进行了仿真，以验证该方法。该方法使用单独的线性状态估计器模型，该模型利用来自WLS的状态估计以及通过后处理的PMU电压和电流测量。首先，该模型使用传统测量的WLS状态估计方法估计极坐标中的状态。然后，该状态和PMU测量值（均以直角坐标表示）用于估计系统的最终状态。保证能运行

在电力系统的研究与运行管理中，准确估计系统状态至关重要。今天咱们就聊聊通过PMU（相量测量单元）测量来估计电力系统状态的方法，并且用Matlab撸个代码实践下，在IEEE - 14总线和IEEE - 30总线系统上仿真验证验证。

方法原理

我们采用的是单独的线性状态估计器模型，这个模型结合了WLS（加权最小二乘）的状态估计成果，同时利用后处理的PMU电压和电流测量数据。

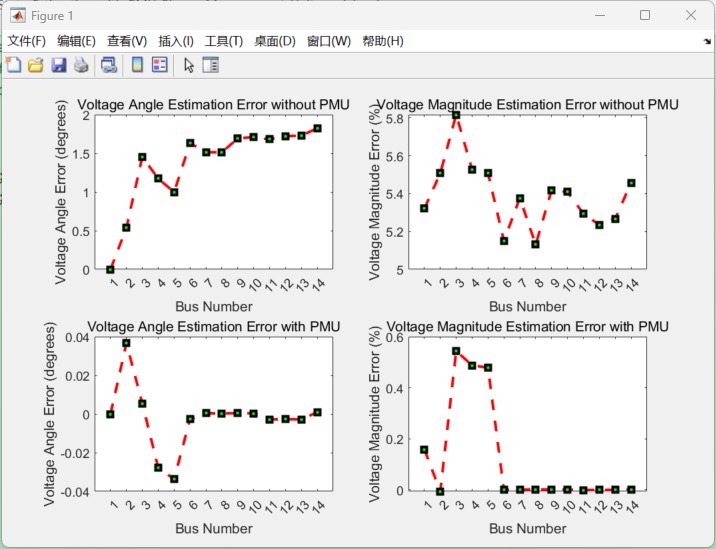
具体来说，先是用传统测量的WLS状态估计方法在极坐标中估计系统状态。假设我们有一系列电力系统的测量值 \(z\)，包含节点电压幅值、相角、支路功率等，这些测量值和系统状态变量 \(x\)（节点电压幅值和相角）存在一定的非线性关系 \(z = h(x) + v\)，其中 \(v\) 是测量噪声。WLS方法就是通过最小化 \(\sum*{i = 1}^{m} w* i (zi - h i(x))^2\) 来求解系统状态 \(x\)，这里 \(wi\) 是对应测量值 \(zi\) 的权重。

然后呢，将这个极坐标下估计出来的状态，和以直角坐标表示的PMU测量值一起，用来估计系统的最终状态。

Matlab代码实现

matlab 复制代码

% 假设已经有IEEE - 14总线或IEEE - 30总线系统的相关参数数据
% 这里以IEEE - 14总线系统为例，简单示意数据读取与处理
busdata = load('IEEE14bus_busdata.txt'); % 假设总线数据存储在这个文件
linedata = load('IEEE14bus_linedata.txt'); % 假设线路数据存储在这个文件

% WLS状态估计部分
% 构建雅可比矩阵和H矩阵
% 这里省略具体构建过程，因为涉及复杂的电力系统模型计算
% 简单假设已经有构建好的H矩阵和权重矩阵W
H = calculate_H_matrix(busdata, linedata); 
W = calculate_W_matrix(busdata, linedata); 

% 测量值z
z = get_measurement_values(busdata, linedata); 

% 初始化状态估计值x_est
x_est = initial_guess(busdata); 

% WLS迭代求解
max_iterations = 100;
tolerance = 1e - 6;
for k = 1:max_iterations
    J = calculate_Jacobian_matrix(x_est); % 计算雅可比矩阵
    residual = z - h(x_est); 
    delta_x = (J' * W * J) \ (J' * W * residual); 
    x_est = x_est + delta_x; 
    if norm(delta_x) < tolerance
        break;
    end
end

% 结合PMU测量估计最终状态
% 假设已经获取到PMU测量值pmu_measurements
pmu_measurements = get_PMU_measurements(); 
% 这里需要将极坐标的x_est转换为直角坐标
x_est_rectangular = polar_to_rectangular(x_est); 
final_state = estimate_final_state(x_est_rectangular, pmu_measurements);

代码分析

数据读取 ：通过 load 函数读取IEEE - 14总线系统的总线数据和线路数据文件，这些数据是后续计算的基础。
WLS状态估计 ：
- 构建相关矩阵：calculateHmatrix 和 calculateWmatrix 函数分别用于构建H矩阵和权重矩阵W，虽然这里省略了具体构建过程，但实际中它们依赖于电力系统的拓扑结构和测量配置。
- 测量值获取：getmeasurementvalues 函数用于从读取的数据中提取测量值 \(z\)。
- 迭代求解：通过循环不断更新状态估计值 \(xest\)，直到满足收敛条件（norm(delta x) < tolerance）。每次迭代中，计算雅可比矩阵 \(J\)，根据测量残差 residual 计算状态修正量 delta_x，进而更新状态估计值。
结合PMU测量 ：
- 坐标转换：polartorectangular 函数将极坐标下的状态估计值转换为直角坐标，以便和直角坐标表示的PMU测量值结合。
- 最终状态估计：estimatefinalstate 函数根据转换后的状态估计值和PMU测量值，估计系统的最终状态。

通过在IEEE - 14总线和IEEE - 30总线系统上运行上述类似的代码，就可以验证我们利用PMU测量估计电力系统状态的方法啦。这样的实践不仅能让我们更深入理解电力系统状态估计的原理，还能通过代码实现提升解决实际问题的能力。希望这篇博文能给研究电力系统状态估计的小伙伴们一些启发。