平面几何：如何绘制一个星形？

大家好，我是前端西瓜哥。

也是有一个月没写文章了。主要是 AI 太强了，简单的东西已经没有写的必要的，复杂的不好写。但多少还是要写点。

今天我们来绘制 Figma 的星形。

星形的绘制，比较简单，其实就是求两个同心圆的内接正多边形的点，将两组点两两连接即可。

方法的参数有：width、height、count、innerScale。方法签名为：

less 复制代码

(
  width: number,
  height: number,
  count: number,
  innerScale: number,
) => Point[];

首先是归一，求出宽高为 1 的矩形下（其实也是半径为 0.5 的原型）的内接多边形的点集。

从最顶部的点开始，不断地旋转 360 / count 的角度，得到 count 个点。中心点是坐标原点。

ini 复制代码

const getInnerRegularPolygon = (radius: number, count: number): Point[] => {
const p = { x: 0, y: -radius };
const points: Point[] = [p];

const dAngle = (Math.PI * 2) / count;

for (let i = 1; i < count; i++) {
    points.push(rotate(p, dAngle * i));
  }

return points;
};

const rotate = (p: Point, rad: number) => {
return {
    x: p.x * Math.cos(rad) - p.y * Math.sin(rad),
    y: p.x * Math.sin(rad) + p.y * Math.cos(rad),
  };
};

这里是基于第一个点，不断地应用一个新的旋转角度。

还有一种方案是基于上一个点，做同样的增量旋转矩阵，但不是很建议，这是一种 "累加" 的策略，会导致误差的累加。

中间步骤越多，误差就累加的越大。类似的有对图形的移动，基于起点的位移会更可靠，基于 mousemove 的上一个点位移则会有很多问题。

接下来是绘制更小内接多边形。

半径改为 innerScale 就好了。innerScale 代表的小圆是相对大圆的大小。

不过起点的位置需要调整下，要顺时针旋转 360 / count / 2 的角度，然后再基于这个点去旋转。

否则你可能得到下面这样一个多边形环。

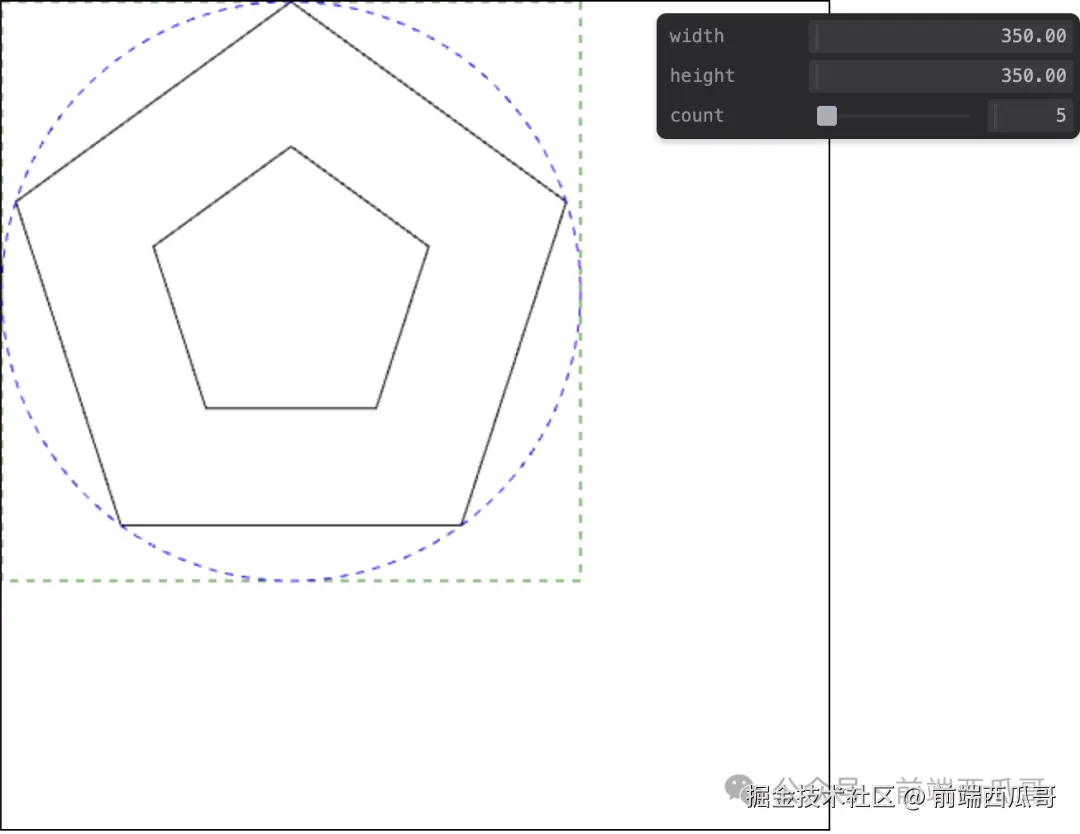
所以需要改造下 getInnerRegularPolygon，提供个起始角度。

ini 复制代码

const getInnerRegularPolygon = (
  radius: number,
  count: number,
  startAngle: number = 0,
): Point[] => {
let p = { x: 0, y: -radius };
if (startAngle) {
    p = rotate(p, startAngle);
  }
const points: Point[] = [p];

const dAngle = (Math.PI * 2) / count;

for (let i = 1; i < count; i++) {
    points.push(rotate(p, dAngle * i));
  }

return points;
};

然后我们得到一个大的正多边形，和一个小的歪了点的正多边形。

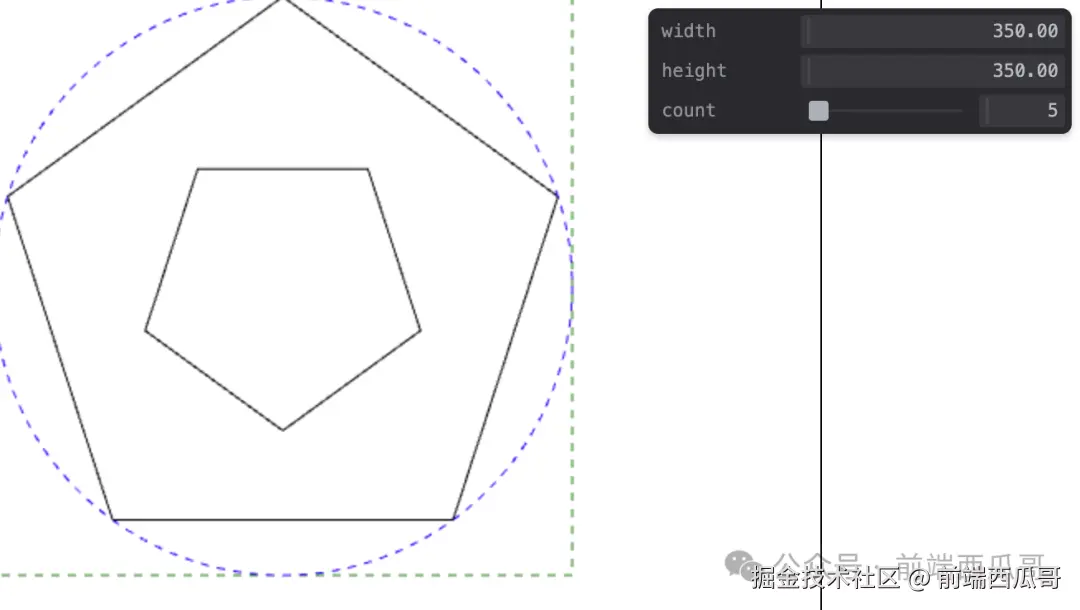
点是对了，就是点的顺序要调整下。我们对大多边形和小多边形的两组点，两两顺排。

ini 复制代码

const outerPoints = getInnerRegularPolygon(1, count);
const innerPoints = getInnerRegularPolygon(
  innerScale,
  count,
  Math.PI / count,
);

const points = [];
for (let i = 0; i < count; i++) {
  points.push(outerPoints[i]);
  points.push(innerPoints[i]);
}

到这里我们绘制了一个 2x2 圆的内接星形。（到这里才发现 1x1 要传入 0.5 或者改多边形算法实现才行，想了下 2x2 也问题不大）

后面我们给这些点放大和位移 就齐活了。scale(width/2, height/2) * translate(width/2, height/2)

ini 复制代码

for (let i = 0; i < points.length; i++) {
  points[i].x = points[i].x * halfWidth + halfWidth;
  points[i].y = points[i].y * halfHeight + halfHeight;
}

return points;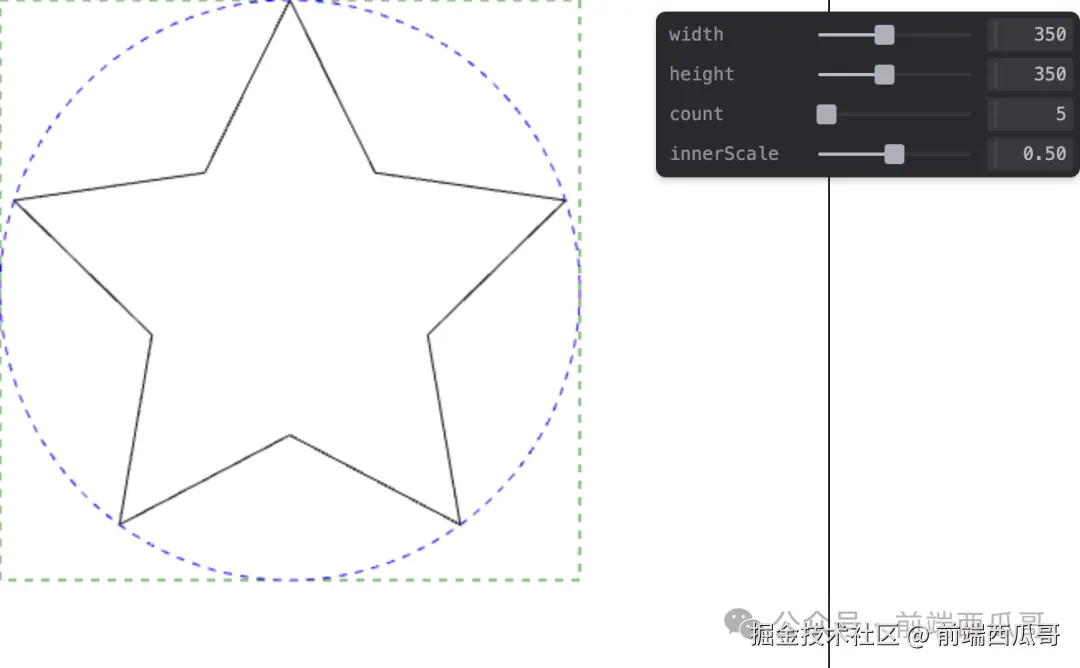

体验

线上体验地址：

geo-play-nv7v.vercel.app/src/page/st...

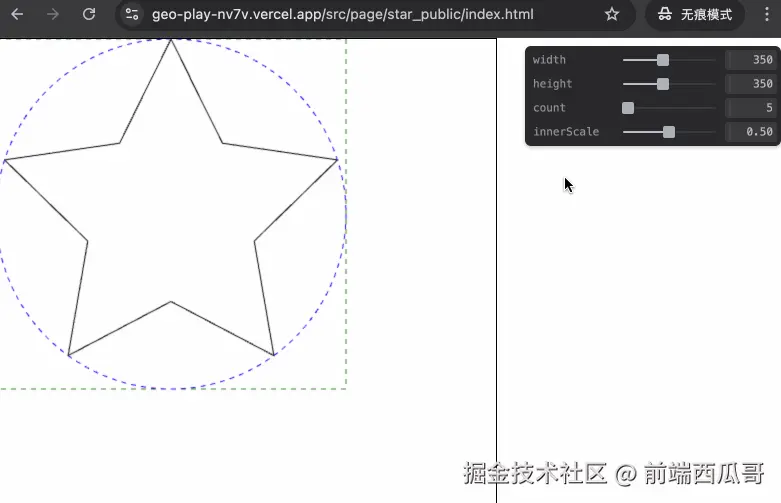
特殊的，innerScale 是 1 的话，就会让 n 角星形变成 2n 多边形。

另外，可以看到，包围盒其实是一个圆形，而不是矩形 ，这就是为什么 Figma 的 星形和多边形在矩形包围盒下会有空隙 的原因。因为包围盒它不是圆形的。

代码实现

ini 复制代码

interface Point {
  x: number;
  y: number;
}

const getInnerRegularPolygon = (
  radius: number,
  count: number,
  startAngle: number = 0,
): Point[] => {
let p = { x: 0, y: -radius };
if (startAngle) {
    p = rotate(p, startAngle);
  }
const points: Point[] = [p];

const dAngle = (Math.PI * 2) / count;

for (let i = 1; i < count; i++) {
    points.push(rotate(p, dAngle * i));
  }

return points;
};

const rotate = (p: Point, rad: number) => {
return {
    x: p.x * Math.cos(rad) - p.y * Math.sin(rad),
    y: p.x * Math.sin(rad) + p.y * Math.cos(rad),
  };
};

exportconst getStarPoints = (
  width: number,
  height: number,
  count: number,
  innerScale: number,
): Point[] => {
const outerPoints = getInnerRegularPolygon(1, count);
const innerPoints = getInnerRegularPolygon(
    innerScale,
    count,
    Math.PI / count,
  );

const points = [];
for (let i = 0; i < count; i++) {
    points.push(outerPoints[i]);
    points.push(innerPoints[i]);
  }

const halfWidth = width / 2;
const halfHeight = height / 2;

// scale(width/2, height/2) * translate(width/2, height/2)
for (let i = 0; i < points.length; i++) {
    points[i].x = points[i].x * halfWidth + halfWidth;
    points[i].y = points[i].y * halfHeight + halfHeight;
  }

return points;
};

结尾

星形，本质是两个多边形的点的交替连接。

几何算法很有趣吧。

我是前端西瓜哥，关注我，学习更多平面几何知识。