每天五分钟：leetcode动态规划-递归与递推_day2

0）先记住一句话（贯穿两种写法）

到第 n 阶的方法数：

最后一步要么走 1 阶：从 n-1 来
要么走 2 阶：从 n-2 来

所以永远是：

f(n) = f(n-1) + f(n-2)

1）递归版本（从"大问题"往下问"小问题"）

✅ 1.1 纯递归（不推荐：会爆炸慢）

想法：我想知道 f(n)，那就去问 f(n-1) 和 f(n-2)。

python 复制代码

def climbStairs(n):
    if n <= 2:
        return n
    return climbStairs(n-1) + climbStairs(n-2)

为什么慢？

因为它会"重复算同一个问题"：

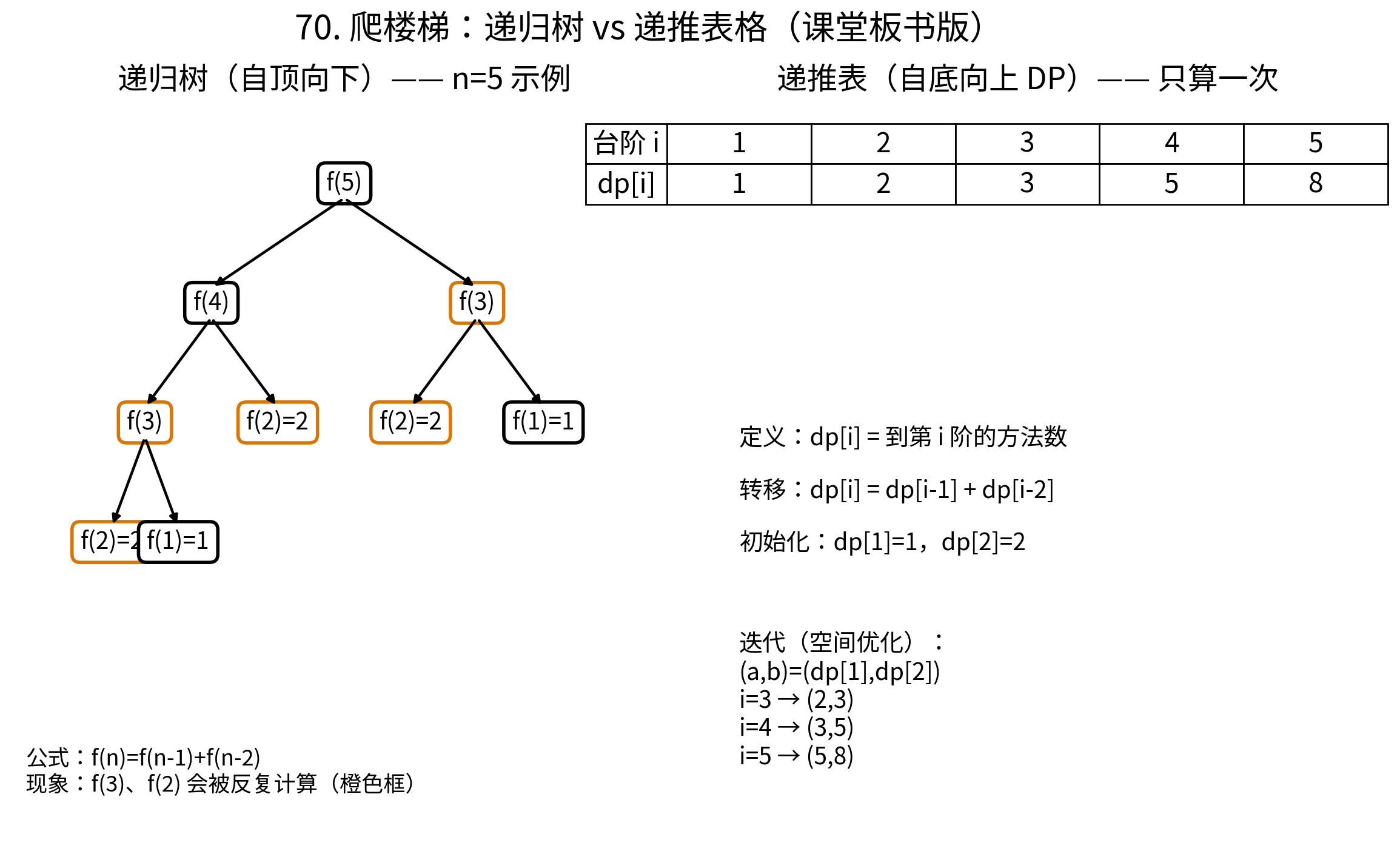
比如算 f(5)：

复制代码

f(5)=f(4)+f(3)

f(4)=f(3)+f(2)

f(3)=f(2)+f(1)

你看：f(3)、f(2) 被算了很多遍。

复杂度 ：接近 O(2^n)，n 稍大就非常慢。

✅ 1.2 递归 + 记忆化（推荐：递归也能很快）

核心：每个 f(k) 只算一次，算过就记下来，下次直接拿。

python 复制代码

def climbStairs(n):
    memo = {}

    def dfs(k):
        if k <= 2:
            return k
        if k in memo:
            return memo[k]
        memo[k] = dfs(k-1) + dfs(k-2)
        return memo[k]

    return dfs(n)

复杂度 ：O(n)

因为 1...n 每个值只算一次。

2）递推版本（从"小问题"一路推到"大问题"）

递推就是：我先知道最小的答案，然后一步步算到 n。

✅ 2.1 DP 数组版（最直观）

python 复制代码

dp[i] 代表到 i 阶的方法数

从 i=3 推到 n

复杂度 ：O(n) 时间，O(n) 空间。

✅ 2.2 空间优化版（你写的版本：最常用

观察转移方程：

dp[i] 只依赖 dp[i-1] 和 dp[i-2]

所以没必要保存整个数组，只保留最近两个数就够了。

python 复制代码

class Solution:
    def climbStairs(self, n: int) -> int:
        if n <= 2:
            return n
        a, b = 1, 2  # dp[1], dp[2]
        for _ in range(3, n + 1):
            a, b = b, a + b
        return b

复杂度 ：O(n) 时间，O(1) 空间。

3）递归 vs 递推：一眼对比

写法	思维方向	是否重复计算	时间复杂度	空间复杂度
纯递归	自顶向下（n→1）	✅会大量重复	O(2^n)	O(n) 递归栈
递归+记忆化	自顶向下（n→1）	❌不重复	O(n)	O(n)
递推 DP 数组	自底向上（1→n）	❌不重复	O(n)	O(n)
递推空间优化	自底向上（1→n）	❌不重复	O(n)	O(1)

4）一句话解释

递归：像问路------"到第 n 阶怎么走？那我先问到 n-1 怎么走，再问到 n-2 怎么走。"
递推：像建楼------"先把 1 阶、2 阶的答案写出来，然后一层层推上去。"