【AAAI-26：时序概念漂移】DeepBooTS：用于时序漂移的双流残差增强

- [1. 一段话总结](#1. 一段话总结)
- [2. 思维导图（mindmap）](#2. 思维导图（mindmap）)
- [3. 详细总结](#3. 详细总结)
- - 一、研究背景与问题
  - 二、核心理论与模型创新
  - - （1）理论依据：偏差-方差视角分析
    - [（2）模型架构：DeepBooTS 双流残差递减提升](#（2）模型架构：DeepBooTS 双流残差递减提升)
  - 三、实验设计与核心结果
- [4. 关键问题与答案](#4. 关键问题与答案)
- - [问题1：DeepBooTS 解决时间序列预测中概念漂移问题的核心逻辑是什么？](#问题1：DeepBooTS 解决时间序列预测中概念漂移问题的核心逻辑是什么？)
  - [问题2：与现有SOTA模型相比，DeepBooTS 的性能优势体现在哪些具体场景？](#问题2：与现有SOTA模型相比，DeepBooTS 的性能优势体现在哪些具体场景？)
  - [问题3：DeepBooTS 的架构设计中，哪些组件是确保其抗漂移、高通用的关键？各组件作用是什么？](#问题3：DeepBooTS 的架构设计中，哪些组件是确保其抗漂移、高通用的关键？各组件作用是什么？)
- 结论

1. 一段话总结

DeepBooTS 是针对时间序列预测中概念漂移 问题提出的双流残差递减提升模型，通过偏差-方差分解理论证明集成学习可在不增加偏差的前提下降低预测方差，核心创新包括输入与标签双流分解、逐层残差校正及门控系数自适应调节，在多元、单变量及大规模数据集上均超越18种SOTA方法，实现 15.8% 的平均性能提升，同时兼具高通用性、可解释性及深度扩展能力（支持16层深度而无过拟合）。

图1:TS预测模型存在概念漂移问题，附录H提供了更多的实验。

复制代码

论文：DeepBoo TS: Dual-Stream Residual Boosting for Drift- Resilient Time-Series Forecasting
作者：Daojun Liang  Jing Chen, Xiao Wang, Yinglong Wang, Shuo Li
单位：Qilu University of Technology (Shandong Academy of Sciences), Qilu Institute of Technology, Case Westem Reserve University
代码：https:/github.com/Anoise/DeepBooTS

请各位同学给我点赞，激励我创作更好、更多、更优质的内容！^_^

关注微信公众号 ，获取更多资讯

2. 思维导图（mindmap）

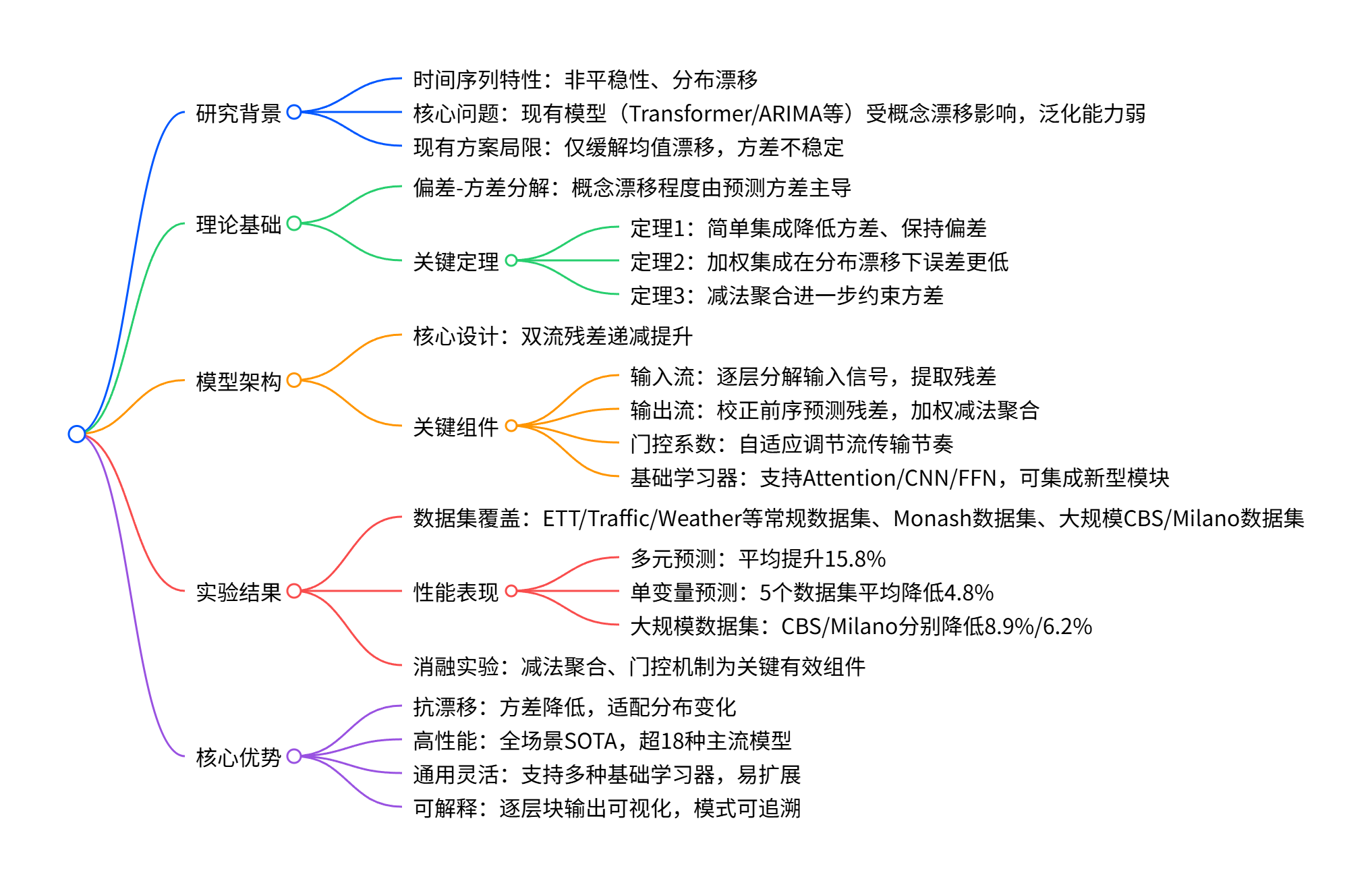
3. 详细总结

时序预测中普遍存在概念漂移问题，即训练数据与实际应用数据分布不匹配，长期困扰着预测模型的鲁棒性，即便当下主流深度学习模型，也常因方差不稳定导致预测误差骤升。

该论文首先通过"偏差-方差分解 "理论证明了当模型的预测偏差与数据噪声固定时，概念漂移的严重程度由预测方差决定 ，同时证明了通过加权集成学习，可在不增加模型偏差的前提下显著降低其方差。基于此，提出了 DeepBooTS（双流残差提升架构） ，其核心在于双流并行学习与残差渐进校正。其中，输入流 用于分解原始数据，输出流 采用分层学习的思想，每一学习器均聚焦前一阶段的预测残差，通过加权减法聚合进一步降低方差，逐步修正预测结果。DeepBooTS在 11 类常用时间序列数据集、7 类 Monash 基准数据集，以及 2 类大规模数据集上对比现有 18 种 SOTA 方法，性能提升了15.8%，大幅降低了预测误差。

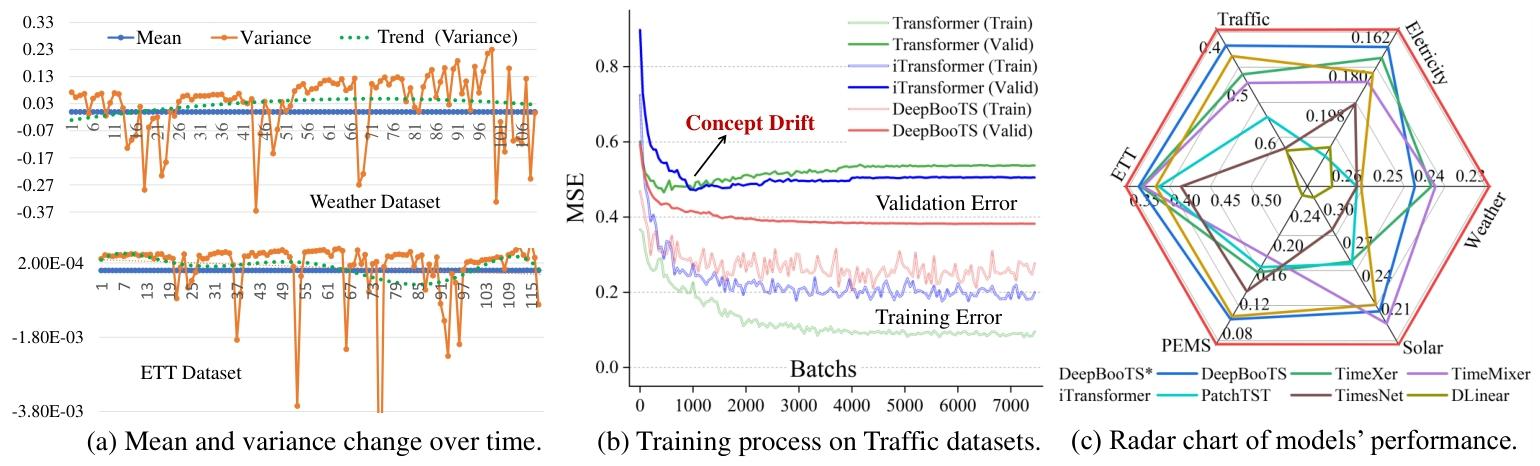
图2:(a)当前TS数据集中存在概念漂移。(b)概念漂移导致模型训练误差减小而验证误差增大。©减少概念漂移后DeepBooTS的性能。

一、研究背景与问题

时间序列（TS）普遍存在非平稳性，导致训练与测试分布不匹配（概念漂移），现有模型（Transformer、ARIMA等）泛化能力受限。
现有解决方案（如RevIN、DLinear）仅缓解均值漂移，方差不稳定仍是核心痛点，导致预测波动大。
深度模型（如Transformer）存在高推理开销，且深度增加易过拟合，难以平衡性能与泛化性。

二、核心理论与模型创新

（1）理论依据：偏差-方差视角分析

核心结论：固定偏差与噪声时，概念漂移程度由预测方差主导。
三大定理支撑：
1. 定理1：简单集成（平均聚合）可降低预测方差，且不增加偏差。
2. 定理2：加权集成在分布漂移下，误差严格低于单一模型。
3. 定理3：减法聚合方式能进一步约束方差，方差上界为 ( \frac{4}{L} \alpha^2 (v+\mu) )（L为块数，v为块误差方差，μ为块间协方差）。

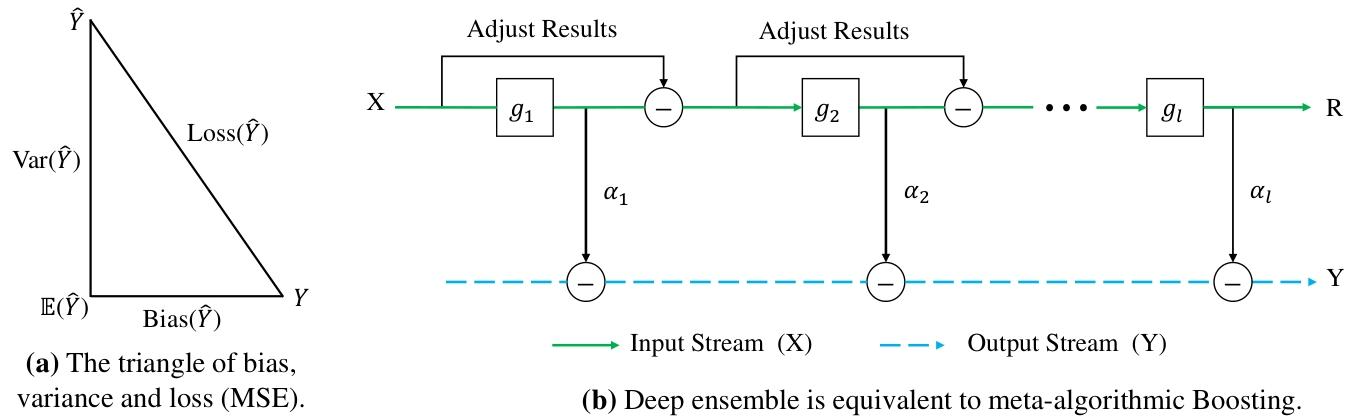
图3:(a)模型偏差、方差和损失之间的关系。(b)深度提升集成学习过程。

（2）模型架构：DeepBooTS 双流残差递减提升

组件	功能描述
双流分解	输入流分解原始信号为残差与有效成分，输出流分解标签为逐层可学习目标
残差校正机制	后续块输出减去前序块预测，逐层降低残差误差，类似梯度提升的深度实现
门控系数	可学习参数调节流传输节奏，适配不同数据模式
基础学习器	支持Attention（含频域FFT优化）、CNN、FFN，可灵活替换新型模块

三、实验设计与核心结果

（1）实验设置

对比模型：18种SOTA方法（iTransformer、PatchTST、Autoformer、Informer等）。
数据集类型：常规数据集（ETT、Traffic、Weather等6类）、Monash数据集（7类）、大规模数据集（CBS：4454节点；Milano：10000节点）。
评价指标：MSE、MAE、MAPE等7种指标，覆盖不同预测长度（96/192/336/720）。

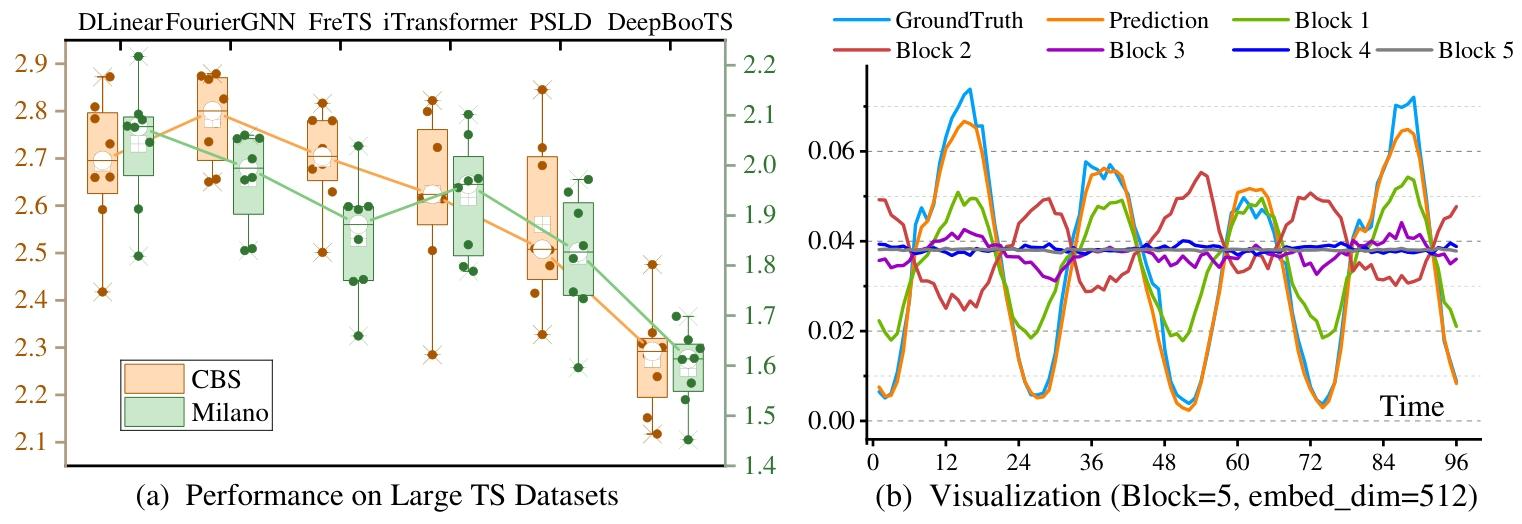
图5:(a)大规模TS数据集的比较。(b)可视化描述DeepBooTS中每个区块的输出。

（2）关键性能结果

任务类型	核心表现
多元时间序列预测	全数据集SOTA，平均性能提升15.8%，ETTm1数据集MSE低至0.029（对比Periodformer 0.033）
单变量时间序列预测	5个数据集平均误差降低4.8%，Traffic数据集输入96-预测96场景MSE从0.143降至0.127（降11.2%）
大规模数据集预测	CBS数据集MSE降低8.9% ，Milano数据集降低6.2%，支持超10000节点场景高效推理
消融实验	减法聚合（-X/-Y）较加法聚合误差降低2.3%-4.9%，门控机制进一步提升性能4.9%

（3）附加优势验证

深度扩展性：块数增至16层无过拟合，而iTransformer块数从4增至8即出现严重过拟合。
超参不敏感：学习率、 batch size 等超参变化时，性能波动小于同类模型。
可解释性：逐层块输出可可视化，能捕捉季节周期、趋势等不同尺度模式。

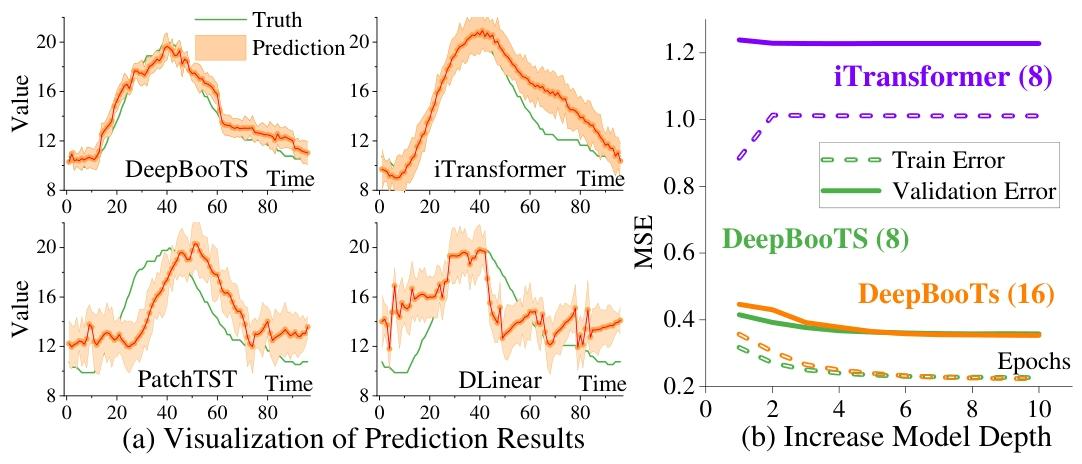
图8：模型方差和深度的比较。

4. 关键问题与答案

问题1：DeepBooTS 解决时间序列预测中概念漂移问题的核心逻辑是什么？

答案：核心逻辑基于偏差-方差分解理论------固定模型偏差与数据噪声时，概念漂移程度由预测方差主导。DeepBooTS 通过集成学习（加权减法聚合）降低预测方差，同时不增加偏差；再结合双流分解（输入与标签逐层分解）和残差校正机制，让模型逐层学习有效模式、降低残差误差，最终实现对分布漂移的适配。

问题2：与现有SOTA模型相比，DeepBooTS 的性能优势体现在哪些具体场景？

答案：性能优势覆盖全场景：① 常规数据集（ETT/Traffic等）：多元预测平均提升15.8%，单变量预测平均降低4.8%；② 大规模数据集（10000节点级）：CBS/Milano数据集MSE分别降低8.9%/6.2%，支持高效推理；③ 长预测长度（720步）：ETTh1数据集MSE低至0.079，显著优于Informer（0.183）；④ 深度扩展：块数增至16层无过拟合，而同类模型（iTransformer）8层即过拟合。

问题3：DeepBooTS 的架构设计中，哪些组件是确保其抗漂移、高通用的关键？各组件作用是什么？

答案：关键组件及作用：① 双流分解：输入流分解原始信号为残差与有效成分，输出流分解标签为可逐层学习目标，实现学习驱动的模式分离；② 减法聚合机制：约束预测方差，方差上界低于加法聚合，直接缓解概念漂移；③ 门控系数：可学习参数自适应调节流传输节奏，适配不同数据模式；④ 灵活基础学习器：支持Attention（含FFT优化）、CNN等，可集成新型模块，提升通用性。

结论

DeepBooTS 通过偏差-方差理论指导，创新双流残差递减提升架构，从根本上缓解概念漂移问题，在常规、大规模、多元/单变量时间序列预测中均实现SOTA性能，同时兼具通用性、可解释性与扩展灵活性，为时间序列预测提供了新范式。