探索多虚拟电厂联合调度优化模型：集中式算法的实践

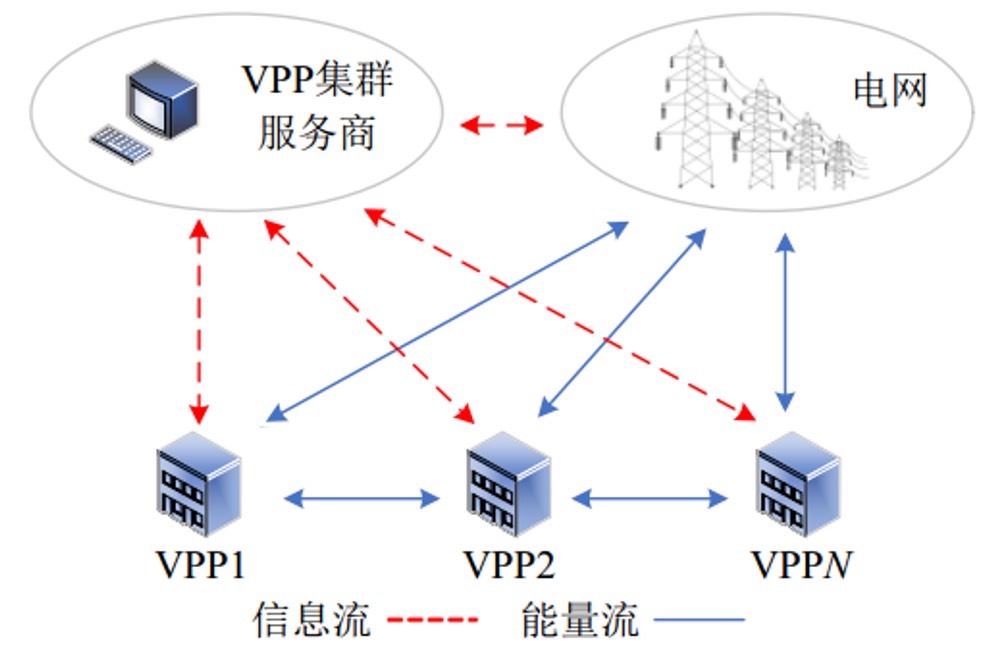
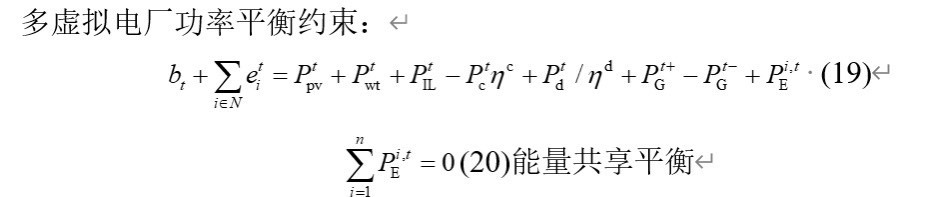（集中式算法）多虚拟电厂联合调度优化模型，包括电动汽车，柔性负荷等，有建模文件，代码根据文件编写，注释清晰。可扩展改写性强，运行平台：matlab+yalmip+cplex 代码一经，不易望理解。

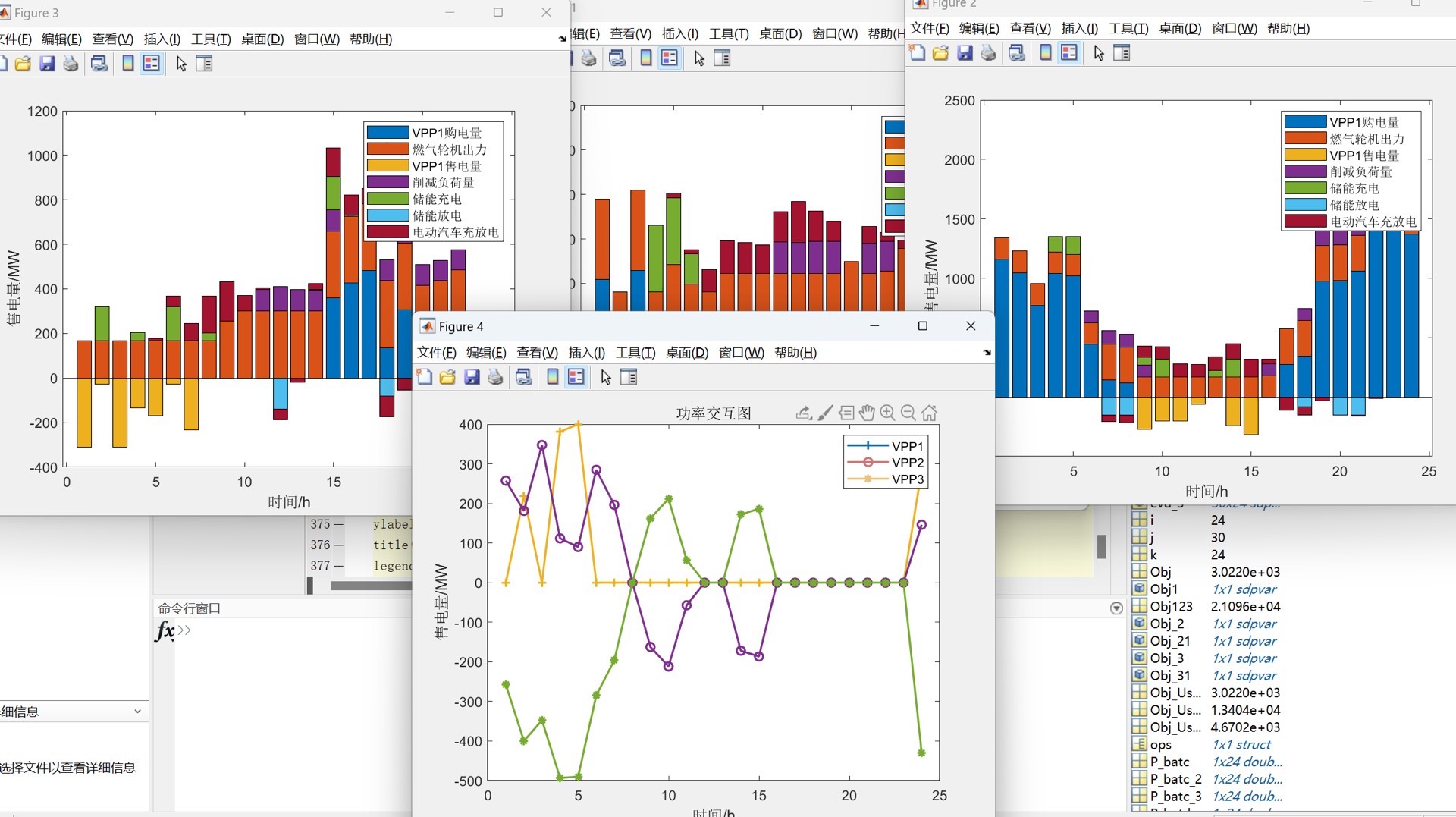
在能源管理领域，多虚拟电厂联合调度优化模型正逐渐成为热门话题。今天咱就唠唠这其中涉及电动汽车、柔性负荷等元素的集中式算法实现，用的平台是 matlab + yalmip + cplex。

建模文件是基石

建模文件为整个代码实现指明了方向。比如说，在考虑电动汽车这一元素时，建模文件会定义电动汽车的充电和放电特性，像充电功率限制、初始电量、不同时段的充放电需求等关键参数。而柔性负荷部分，则会刻画其可调节的范围、调节速度以及不同时段的响应特性。这些细致的模型定义，就像是建筑蓝图，让后续代码编写有的放矢。

Matlab 代码实战

matlab 复制代码

% 1. 参数定义
% 假设虚拟电厂数量为 N
N = 3; 
% 时段数量为 T
T = 24; 

% 电动汽车相关参数
EV_charging_rate = 5; % 充电功率 5kW
EV_discharging_rate = 4; % 放电功率 4kW
EV_max_charge = 30; % 最大充电量 30kWh
EV_max_discharge = 20; % 最大放电量 20kWh

% 柔性负荷相关参数
flexible_load_min = 10; % 最小负荷 10kW
flexible_load_max = 50; % 最大负荷 50kW
flexible_load_adjust_rate = 0.2; % 负荷调节速率 20%

% 2. 变量声明
% 虚拟电厂出力
P_VPP = sdpvar(N, T); 
% 电动汽车充电量
P_EV_charge = sdpvar(1, T); 
% 电动汽车放电量
P_EV_discharge = sdpvar(1, T); 
% 柔性负荷调节量
P_flexible_load = sdpvar(1, T); 

% 3. 约束条件
Constraints = [];

% 虚拟电厂出力限制
for n = 1:N
    for t = 1:T
        Constraints = [Constraints, P_VPP(n, t) >= 0];
        Constraints = [Constraints, P_VPP(n, t) <= 100]; % 假设最大出力 100kW
    end
end

% 电动汽车充放电约束
for t = 1:T
    Constraints = [Constraints, P_EV_charge(t) >= 0];
    Constraints = [Constraints, P_EV_charge(t) <= EV_max_charge];
    Constraints = [Constraints, P_EV_discharge(t) >= 0];
    Constraints = [Constraints, P_EV_discharge(t) <= EV_max_discharge];
    Constraints = [Constraints, P_EV_charge(t) * EV_charging_rate - P_EV_discharge(t) * EV_discharging_rate <= 0]; % 电量平衡约束简化版
end

% 柔性负荷约束
for t = 1:T
    Constraints = [Constraints, P_flexible_load(t) >= flexible_load_min];
    Constraints = [Constraints, P_flexible_load(t) <= flexible_load_max];
    if t > 1
        Constraints = [Constraints, abs(P_flexible_load(t) - P_flexible_load(t - 1)) <= flexible_load_max * flexible_load_adjust_rate];
    end
end

% 4. 目标函数 - 假设最小化总发电成本
Cost_VPP = sum(sum(P_VPP)); % 简单假设发电成本与出力成正比
Cost_EV = sum(P_EV_charge * 0.5 + P_EV_discharge * 0.3); % 充电和放电成本假设
Cost_flexible_load = sum(P_flexible_load * 0.2); % 柔性负荷调节成本假设
Objective = Cost_VPP + Cost_EV + Cost_flexible_load;

% 5. 求解
ops = sdpsettings('solver', 'cplex');
sol = optimize(Constraints, Objective, ops);

% 6. 结果展示
if sol.problem == 0
    disp('优化成功');
    disp('虚拟电厂出力:');
    disp(value(P_VPP));
    disp('电动汽车充电量:');
    disp(value(P_EV_charge));
    disp('电动汽车放电量:');
    disp(value(P_EV_discharge));
    disp('柔性负荷调节量:');
    disp(value(P_flexible_load));
else
    disp('优化失败');
end

代码分析

参数定义部分 ：我们先明确了模型中的各种关键参数，比如虚拟电厂数量 N、时段数量 T，以及电动汽车和柔性负荷的特性参数。这一步是为后续变量和约束条件设置做准备。
变量声明 ：用 sdpvar 声明了我们需要求解的变量，包括虚拟电厂出力 PVPP*、电动汽车充放电量 P* EVcharge**和 P EVdischarge*，以及柔性负荷调节量 P* flexible_load。这些变量就是模型要找的最优解。
约束条件 ：
- 虚拟电厂出力限制，保证每个虚拟电厂在各个时段的出力在合理范围内。
- 电动汽车充放电约束，不仅限制了充放电量，还简单考虑了电量平衡。
- 柔性负荷约束，确保负荷在允许范围，并且考虑了调节速率限制。
目标函数：这里假设最小化总发电成本，把虚拟电厂发电成本、电动汽车充放电成本和柔性负荷调节成本都加起来。不同成本的权重假设是根据实际情况预估的，实际应用中可以调整。
求解与结果展示 ：使用 optimize 函数，结合 cplex 求解器，根据我们设定的约束和目标来求解。最后根据求解结果输出相应信息，如果成功就展示各个变量的最优值。

整个模型的代码可扩展改写性强。要是以后考虑更多的虚拟电厂特性，比如不同的发电成本函数，或者更复杂的电动汽车电池寿命损耗模型，都可以在现有基础上轻松修改。

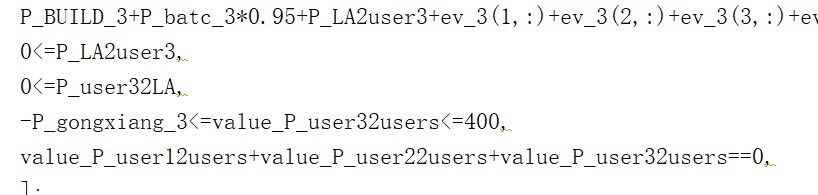
总之，这个多虚拟电厂联合调度优化模型通过合理的建模和代码实现，在 matlab + yalmip + cplex 平台上为能源调度提供了一种有效的解决方案。