用三次样条插值法求解信号包络线的Matlab实现

三次样条插值法求解信号包络线，内容为matlab程序。

在信号处理领域，我们常常需要获取信号的包络线，这对于分析信号的特性、提取关键信息至关重要。三次样条插值法是一种非常有效的求解信号包络线的方法，今天咱们就来聊聊如何用Matlab实现它。

三次样条插值法原理简述

三次样条插值是在给定的离散数据点之间构造一个分段的三次多项式函数。它要求在每个数据点上函数值与给定值相等，并且在节点处函数的一阶导数和二阶导数连续。简单理解，就是让构造的曲线不仅经过已知点，还能平滑过渡，这样就可以很好地拟合出信号的包络线。

Matlab 程序实现

下面直接上代码：

% 生成示例信号数据
t = 0:0.01:1; % 时间向量，从0到1，步长0.01
y = 2 * sin(2 * pi * 5 * t) + sin(2 * pi * 15 * t); % 复合正弦信号

% 寻找信号的峰值点
[pks, locs] = findpeaks(y); % findpeaks函数找到信号的峰值及位置

% 三次样条插值
pp = spline(locs, pks); % 使用spline函数进行三次样条插值

% 插值后的包络线数据
t_interp = 0:0.001:1; % 更密集的时间向量用于绘制光滑包络线
y_envelope = ppval(pp, t_interp); % 通过ppval函数计算插值后的包络线值

% 绘图
figure;
plot(t, y, 'b', 'DisplayName', '原始信号'); hold on;
plot(t_interp, y_envelope, 'r--', 'DisplayName', '包络线');
scatter(locs, pks, 'filled', 'DisplayName', '峰值点');
legend;
title('三次样条插值法求解信号包络线');
xlabel('时间 t (s)');
ylabel('幅值');

代码分析

1. 生成示例信号数据：

t = 0:0.01:1; 
y = 2 * sin(2 * pi * 5 * t) + sin(2 * pi * 15 * t); 

这里我们首先定义了一个时间向量 t，从 0 到 1，步长为 0.01。然后构建了一个复合正弦信号 y，由两个不同频率的正弦波叠加而成，这就是我们要处理的原始信号。

1. 寻找信号的峰值点：

[pks, locs] = findpeaks(y); 

Matlab 的 findpeaks 函数非常方便，它直接帮我们找出了信号 y 中的峰值 pks 以及对应的时间位置 locs。这些峰值点是构建包络线的关键数据点。

1. 三次样条插值：

pp = spline(locs, pks); 

Spline 函数以峰值点的位置 locs 和峰值 pks 作为输入，返回一个分段多项式结构体 pp。这个结构体包含了构建三次样条插值曲线所需的所有信息。

1. 插值后的包络线数据：

t_interp = 0:0.001:1; 
y_envelope = ppval(pp, t_interp); 

为了绘制出更光滑的包络线，我们定义了一个更密集的时间向量 tinterp*，步长为 0.001。然后通过 ppval 函数，根据之前得到的分段多项式结构体 pp，计算出在 t* interp 各时间点上的包络线值 y_envelope。

1. 绘图：

figure;
plot(t, y, 'b', 'DisplayName', '原始信号'); hold on;
plot(t_interp, y_envelope, 'r--', 'DisplayName', '包络线');
scatter(locs, pks, 'filled', 'DisplayName', '峰值点');
legend;
title('三次样条插值法求解信号包络线');
xlabel('时间 t (s)');
ylabel('幅值');

最后，我们使用 plot 函数分别绘制原始信号、包络线，并用 scatter 函数标记出峰值点。hold on 确保多个图形能在同一坐标系中显示。通过添加标题、坐标轴标签和图例，让图形更加清晰易读。

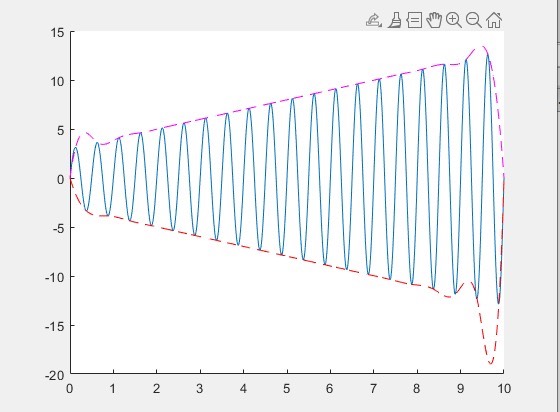
通过以上Matlab程序，我们就能利用三次样条插值法轻松求解信号的包络线啦，希望这能帮大家在信号处理相关工作中有所助力。