每天五分钟：动态规划-LeetCode高频题_day2

下面这 4 道题本质都是 动态规划 DP：DP 定义 → 转移方程 → 初始化 → 代码

70. 爬楼梯

借本题，写一下动态规划问题中的 "递归与递推" ~

118. 杨辉三角

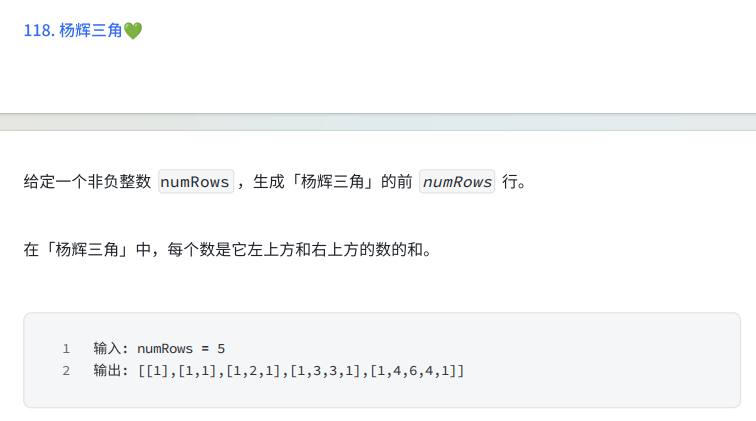
TIPS:每个位置的数 = 它左上方 + 右上方。边上永远是 1。

DP 思路

第 r 行（从 0 开始）有 r+1 个数
边界：row[0]=row[-1]=1
中间：row[j] = prev[j-1] + prev[j]

python 复制代码

class Solution:
    def generate(self, numRows: int):
        res = []
        for r in range(numRows):
            row = [1] * (r + 1)
            for j in range(1, r):
                row[j] = res[r-1][j-1] + res[r-1][j]
            res.append(row)
        return res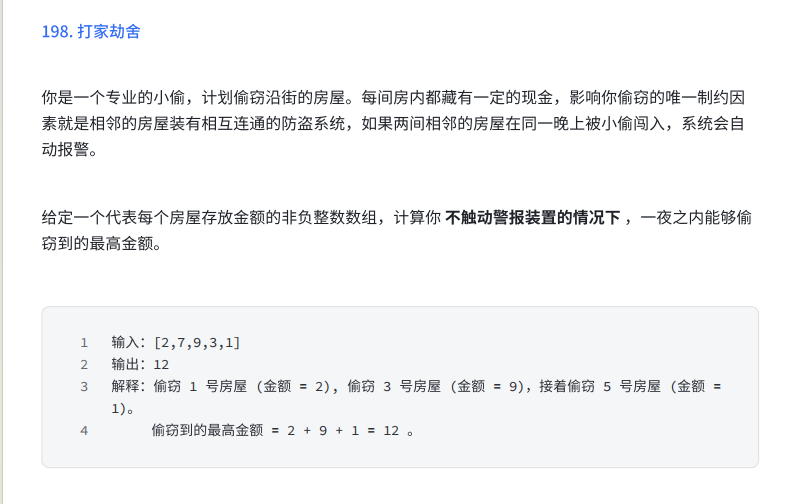

198. 打家劫舍

DP 思路

dp $i$ ：偷到第 i 间房（下标 i）为止的最大金额
第 i 间有两种选择：
1. 不偷第 i 间：dp[i] = dp[i-1]
2. 偷第 i 间：dp[i] = dp[i-2] + nums[i]
转移方程 ：dp[i] = max(dp[i-1], dp[i-2] + nums[i])
初始化：
- dp[0]=nums[0]
- dp[1]=max(nums[0], nums[1])

python 复制代码

class Solution:
    def rob(self, nums):
        prev2, prev1 = 0, 0  # dp[i-2], dp[i-1]
        for x in nums:
            cur = max(prev1, prev2 + x)
            prev2, prev1 = prev1, cur
        return prev1

279. 完全平方数

最少块数 = "枚举最后一块平方数"

DP 思路（把大问题拆成小问题）

状态定义

dp[i]：拼出数字 i 的最少平方数块数

最后一步怎么来？

假设最后拿的是一块 j*j（比如 1、4、9、16...）

那拼出 i 就等于：

先拼出 i - j*j，再加上这 1 块 j*j

所以候选答案是：

dp[i - j*j] + 1

python 复制代码

class Solution:
    def numSquares(self, n: int) -> int:
        """
        使用动态规划求解"完全平方数"问题
        目标：找到最少的完全平方数（如 1, 4, 9, 16, ...）使其和等于 n
        """
        
        # dp[i] 表示拼出数字 i 所需的最少完全平方数的个数
        # 初始化 dp[0] = 0（拼出 0 需要 0 个平方数）
        # 其他位置初始化为一个较大的值（这里用 10**9 表示无穷大），
        # 因为我们要寻找最小值，所以初始化为大数以便后续用 min 更新
        dp = [0] + [10**9] * n    #dp = [0] + [10**9 for _ in range(n)]

        # 从 1 到 n 依次计算每个 dp[i] 的值
        for i in range(1, n + 1):
            j = 1
            # 尝试所有小于等于 i 的完全平方数 j*j
            while j * j <= i:
                sq = j * j  # 当前尝试的完全平方数
                # 关键递推关系：
                # 要拼出 i，可以从 (i - sq) 的基础上再加一个平方数 sq
                # 因此候选方案是 dp[i - sq] + 1
                # 从所有可能的 sq 中选出最小值
                dp[i] = min(dp[i], dp[i - sq] + 1)
                j += 1

        # dp[n] 即为拼出 n 所需的最少完全平方数个数
        return dp[n]

# 示例说明：
# 输入 n = 12
# 计算过程：
# dp[0]=0
# i=1: j=1, sq=1 -> dp[1] = min(∞, dp[0]+1) = 1
# i=2: j=1, sq=1 -> dp[2] = min(∞, dp[1]+1) = 2
# i=3: j=1, sq=1 -> dp[3] = min(∞, dp[2]+1) = 3
# i=4: j=1, sq=1 -> dp[4] = min(∞, dp[3]+1) = 4
#      j=2, sq=4 -> dp[4] = min(4, dp[0]+1) = 1 （更新为更优解）
# i=12: 最终 dp[12] 会从 dp[12-9]+1=dp[3]+1=4 和 dp[12-4]+1=dp[8]+1 等方案中选出最小值 3（4+4+4）
# 输出: 3

# 时间复杂度: O(n * sqrt(n))，外层循环 n 次，内层最多 sqrt(n) 次
# 空间复杂度: O(n)，用于存储 dp 数组