文章目录
如果细说的话,这个专题应该叫推公式+排序。其中推公式就是寻找排序规则,排序就是在该排序规则下对整个对象排序。
在解决某些问题的时,当我们发现最终结果需要调整每个对象的先后顺序,也就是对整个对象排序时,那么我们就可以⽤推公式的⽅式,得出我们的排序规则,进⽽对整个对象排序。
正确性证明:利⽤排序解决问题,最重要的就是需要证明"在新的排序规则下,整个集合可以排序"。这需要⽤到离散数学中"全序关系"的知识,也就是需要证明排序的比较器cmp具有全序关系。小编会在第⼀道题中证明该题的排序规则下,整个集合是可以排序的。
但是证明过程很⿇烦,后续题⽬中我们只要发现该题最终结果需要排序,并且交换相邻两个元素的时候,对其余元素不会产⽣影响,那么我们就可以推导出排序的规则,然后直接去排序,就不去证明了。
拼数
题目描述
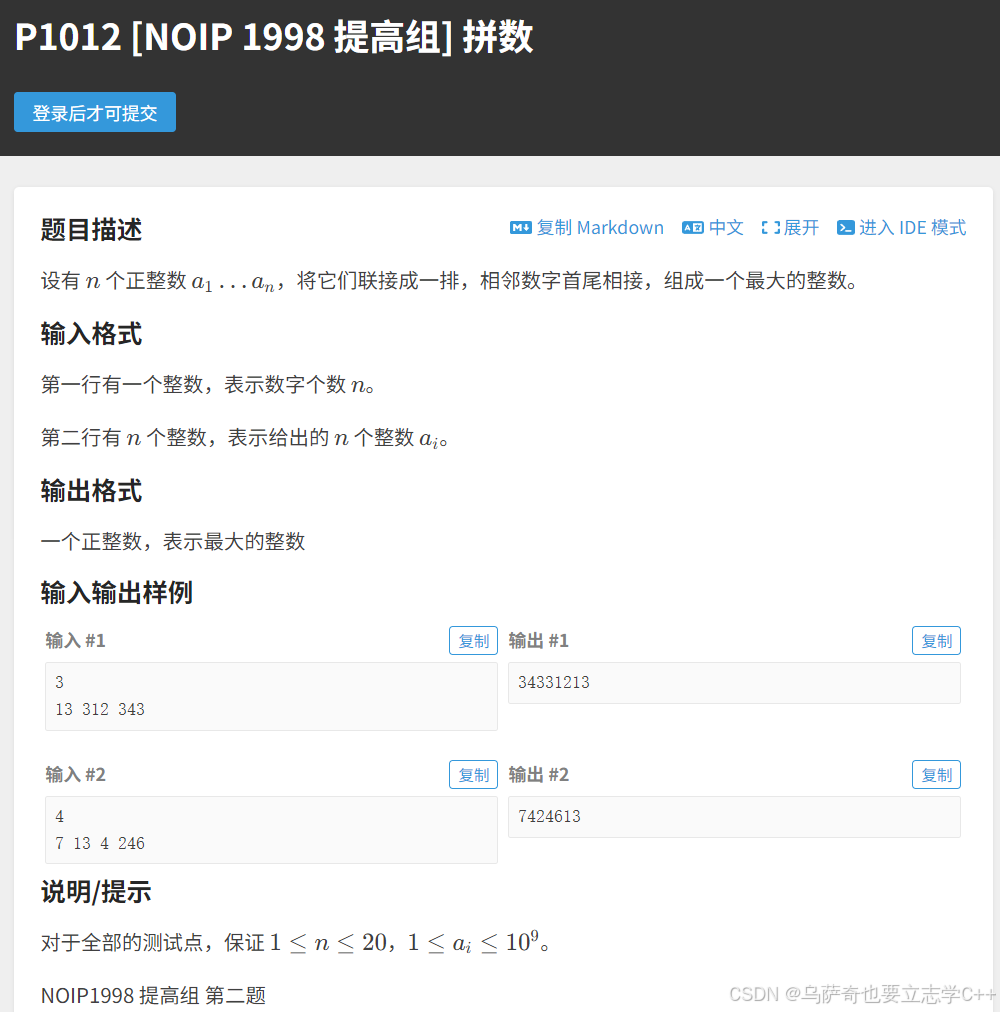
题目解析
本题我们最先能想到的策略就是通过字典序进行排序,但是这种策略是错误的,比如543和54进行拼接,根据字典序543比54大,那么543在前,54在后就会拼接出54354,但是54354并不是最大值,最大值应该是54在前,543在后的54543。
所以本题的策略应该把数直接拼接,然后比较大小确定拼接的前后关系,最后结合排序确定最终序列的前后顺序。
1、比较方法如下: ab > ba,a在前,b在后 ab < ba,b在前,a在后 ab = ba,a、b顺序无所谓。
2、排序利用algorithm的sort。(补充:sort 函数会根据 cmp(sx, sy) 的返回值决定 sx 是否应该排在 sy 前面 ------ 返回 true 则 sx 在前,返回 false 则 sy 在前)
下面我们需要证明两点:1、这个新的排序规则是否可以排序,这里就需要用到全序关系的知识。
2、这个贪心策略是否正确,这个证明非常啰嗦也不重要小编就不证明了。
下面我们来证明第一点,首先明确全序关系是什么:1、完全性:任意两个元素可以进行大小比较。
2、反对称性:当 a <= b 且 a >= b 时要能推出 a = b,也就是当a b相等时它们的先后顺序是无所谓的。
3、传递性:a > b, b > c 能推出 a > c 说明具有传递性。
证明本题的集合具有全序关系:完全性:
我们需要证明ab和ba是能比较大小的,最佳思路就是把ab和ba转化成两个整型变量,我们设a的位数是x,b的位数是y,那么ab就可以转化成a * 10^y + b,ab就可以转化成b * 10^x + a,都转换成整型变量就可以进行大小比较了。(为了证明严谨,本题中我们可以把0当作一位数,方便计算,但是小编要提醒各位一个细节,在我们实际研究整数的时候0是没有位数的,因为如果0是一位数的话,那么00就是两位数,这样的话最小的两位数就是00了,但是实际上最小的两位数是10。)
反对称性:
当我们把ab和ba转化成两个整型变量后,整型变量本身就具有反对称性了: a * 10^y >= b * 10^x + a,并且 a * 10^y <= b * 10^x + a 是能推出 a * 10^y == b * 10^x + a 的。
传递性:
证明同反对称性。
代码
cpp
#include <iostream>
#include <string>
#include <algorithm>
using namespace std;
const int N = 25;
string a[N];
bool cmp(string& s1, string& s2)
{
return s1 + s2 > s2 + s1;
}
int main()
{
int n;
cin >> n;
//初始化数据
for (int i = 1; i <= n; i++)
{
cin >> a[i];
}
//排序
sort(&a[1], &a[n + 1], cmp);
//输出结果
for (int i = 1; i <= n; i++)
{
cout << a[i];
}
cout << endl;
return 0;
}ProtectingtheFlowersS
题目描述
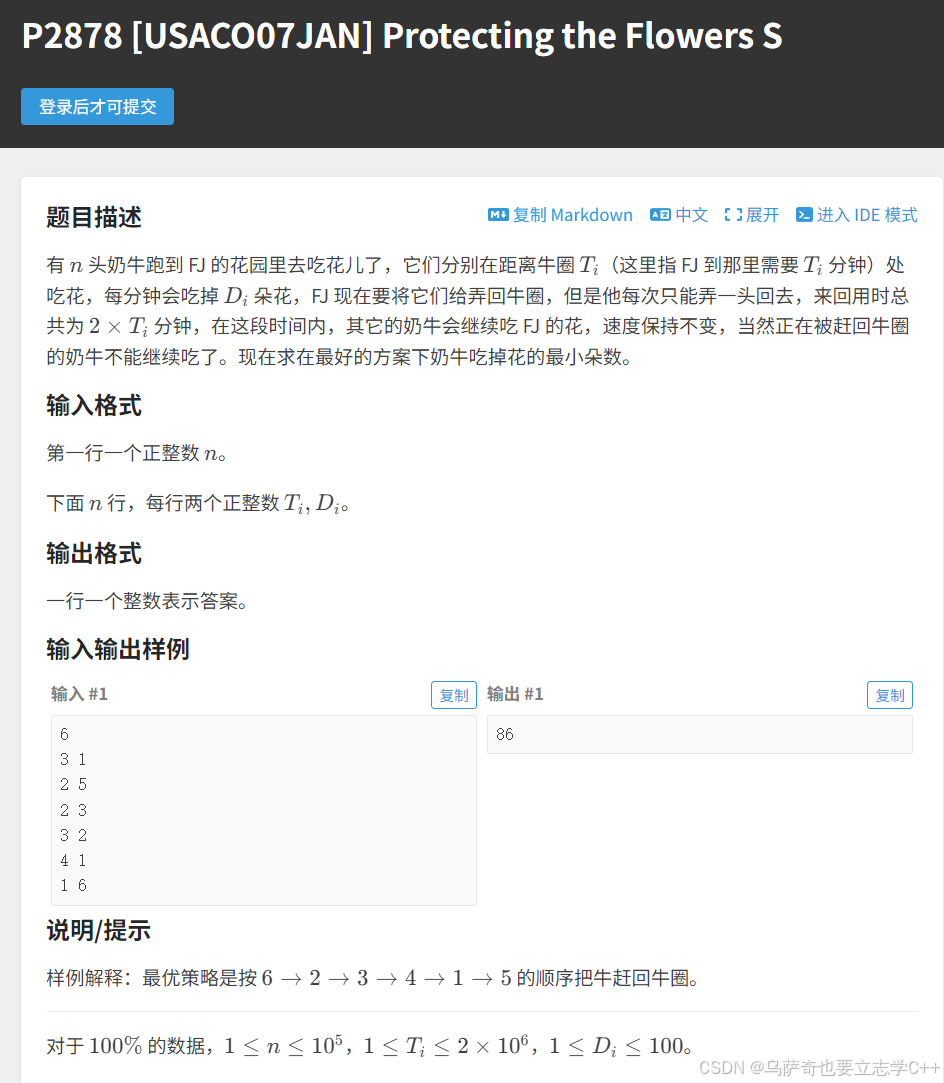
题目解析
自己的思路:
把每一头牛的Ti和Di用数组存储,Ti从小到大排序,Di从大到小排序,越靠前数组下标越小权值越高,再将每头牛的Ti和Di的数组下标和按从小到大排序,按该顺序依次抓牛。
解题思路:上一题推公式很简单,不具有普适性,本题小编会教大家推公式的通用思路,方便遇到类似题目举一反三。
本题最终结果就是需要确定牵牛顺序,因此,就需要对所有奶牛进行排序,所以本题核心就是找到排序规则,要找到排序规则,就需要进行推公式,推公式基本思路如下:
1、在确定好顺序的序列中拿出两个相邻的元素。
2、如果交换这两个元素后对前面以及后面已经排好序的序列的结果不造成影响。
3、此时就可以通过这两个元素交换前后的结果推导出排序规则,也就是推出cmp比较器的逻辑(满足什么条件i在j的前面)。
以本题为例,我们选出排好序的序列中两个相邻的奶牛i和j,它们俩距离牛圈的距离分别是ti和tj,每分钟分别吃掉di和dj朵花,在它们前面的所有已经排好序的奶牛全部被赶回牛圈需要消耗的时间是T1,吃掉的总花朵数是D1,在它们后面的所有已经排好序的奶牛全部被赶回牛圈需要消耗的时间是T2,吃掉的总花朵数是D2,当i和j交换后并不会影响T1、D1、T2、D2,所以符合"交换这两个元素后对前面以及后面已经排好序的序列的结果不造成影响",接下来我们就开始推公式:

如上图所示,i在前j在后我们可以推出吃掉的总花朵数sum1,i在后j在前我们可以推出吃掉的总花朵数sum2,我们要推的比较器逻辑需要让i在前,j在后,所以就需要让sum1 < sum2,据此我们可以推出比较器逻辑:
dj * ti < di * tj
注意本题计算结果时需要用一个变量t存放下一头奶牛的总吃花时间,据此变量排好序的序列得出最终结果。
代码
cpp
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N = 1e5 + 10;
pair<int, int> a[N]; // <Ti, Di>
bool cmp(pair<int, int>& p1, pair<int, int>& p2)
{
// i在前,j在后,Dj*Ti < Di*Tj
return p2.second * p1.first < p1.second * p2.first;
}
int main()
{
int n;
cin >> n;
//初始化
for(int i = 1; i <= n; i++)
{
cin >> a[i].first >> a[i].second;
}
//排序
sort(&a[1], &a[n + 1], cmp);
//输出结果
LL ret = 0; //最小被吃花朵数
//存放下一头奶牛的总吃花时间,初始化为0因为第一头奶牛没有机会吃花
int t = 0;
for (int i = 1; i <= n; i++)
{
ret += a[i].second * t;
t += 2 * a[i].first;
}
cout << ret << endl;
return 0;
}奶牛玩杂技
题目描述
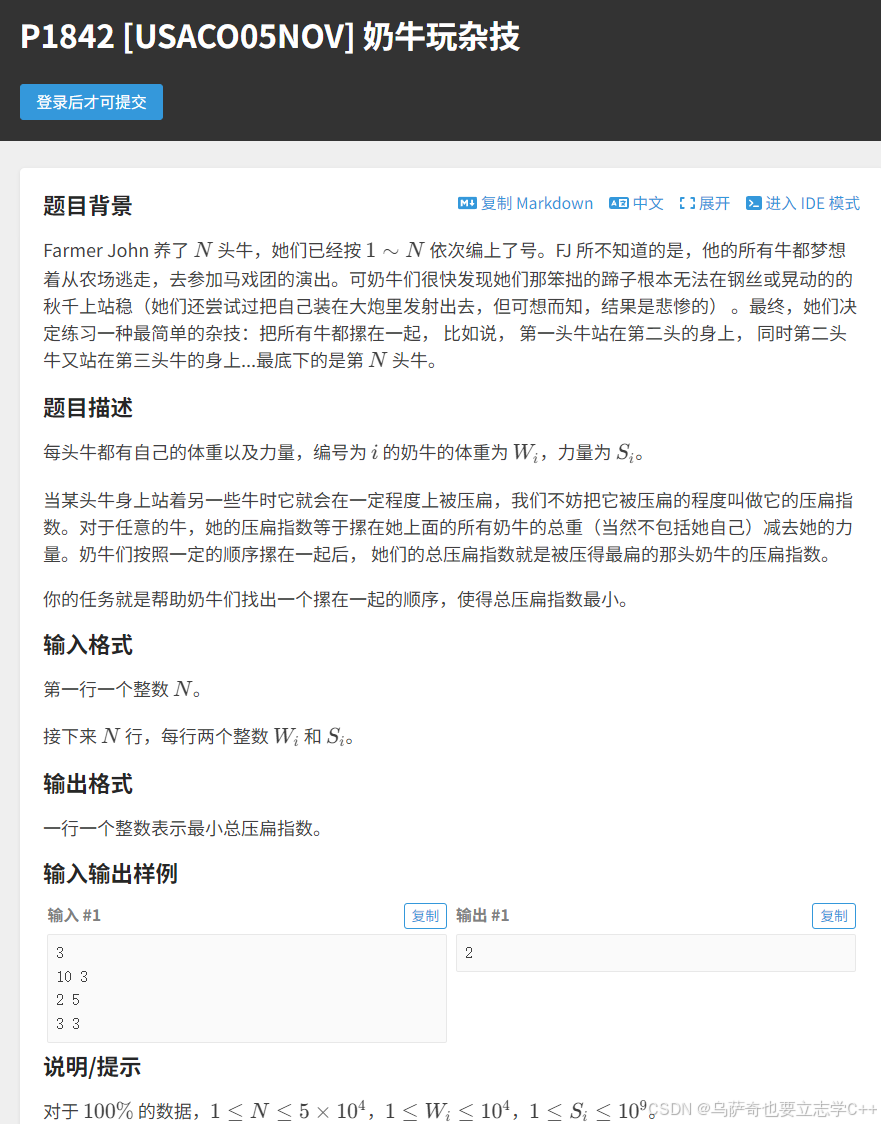
题目解析
没写出正确答案原因及原始代码: 没有搞清楚核心比较逻辑,比较逻辑应该是让i在前j在后需要满足什么条件。
解题思路: 首先需要注意,压扁指数是w - s,被压的最扁说明 w - s 值最大,求总压扁指数最小就转化成了最大值最小化问题。
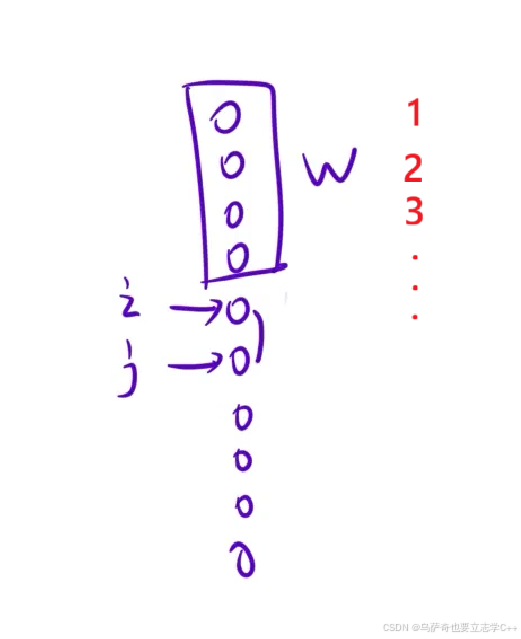
依旧延续第二题的思路,要让总压扁指数小就需要让每次比较的两个元素都能取到更小的压扁指数,这就是我们常说的局部最优推导全局最优。在已经排好序的序列中选出两个相邻的元素i和j,奶牛i重wi,力量是si,奶牛j重wj,力量是sj,在它们上面的奶牛总重是w,假设i在j前时能取到更小的压扁指数,也就是:
max(w - si, w + wi - sj) < max(w + wj - si, w - sj)
max(w - si, w + wi - sj) 是i在j前时能取到的最大压扁指数,w - si 表示i的压扁指数,w + wi - sj 表示j的压扁指数,max(w + wj - si, w - sj)同理,比较逻辑就是如果i在j前时能取到的最大压扁指数比j在i前时能取到的最大压扁指数更小,那么就让i排j前,反之让j排i前。
代码
cpp
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 5e4 + 10;
struct node
{
int w;
int s;
}a[N];
bool cmp(node& n1, node& n2)
{
return max(-n1.s, n1.w - n2.s) < max(n2.w - n1.s, -n2.s);
}
int main()
{
int n;
cin >> n;
//初始化数据
for (int i = 1; i <= n; i++)
{
cin >> a[i].w >> a[i].s;
}
//排序
sort(&a[1], &a[n + 1], cmp);
//输出结果
int ret = -0x3f3f3f3f;
int weight = 0; //当前牛上面的牛的总重
for (int i = 1; i <= n; i++)
{
ret = max(ret, weight - a[i].s);
weight += a[i].w;
}
cout << ret << endl;
return 0;
}总结
推公式本质就是要推出比较器cmp的逻辑,i排在j前需要满足什么条件:
比如第二题需要满足:
sum1 < sum2
第三题需要满足:
max(w - n1.s, w + n1.w - n2.s) < max(w + n2.w - n1.s, w - n2.s)