文章目录
- 说明
- [一 数组](#一 数组)
-
- [1.1 访问数组元素](#1.1 访问数组元素)
- [1.2 数组循环递增](#1.2 数组循环递增)
- [1.3 多层(嵌套)数组](#1.3 多层(嵌套)数组)
-
- [1.3.1 行向量访问](#1.3.1 行向量访问)
- [1.3.2 嵌套数组元素访问](#1.3.2 嵌套数组元素访问)
- [1.4 多级数组表示](#1.4 多级数组表示)
- [1.5 数组元素访问对比](#1.5 数组元素访问对比)
- [二 结构体(重点)](#二 结构体(重点))
-
- [2.1 结构体内存对齐规则](#2.1 结构体内存对齐规则)
- [2.2 内存对齐:为何重要?](#2.2 内存对齐:为何重要?)
- [2.3 通过结构体实现对齐](#2.3 通过结构体实现对齐)
- [2.4 结构体数组和元素访问](#2.4 结构体数组和元素访问)
- [2.5 成员排序优化](#2.5 成员排序优化)
- [2.6 结构体对齐考试题(重点)](#2.6 结构体对齐考试题(重点))
说明
- 庄老师的课堂,如春风拂面,启迪心智。然学生愚钝,于课上未能尽领其妙,心中常怀惭愧。
- 幸有课件为引,得以于课后静心求索。勤能补拙,笨鸟先飞,一番沉浸钻研,方窥见知识殿堂之幽深与壮美,竟觉趣味盎然。
- 今将此间心得与笔记整理成篇,公之于众,权作抛砖引玉。诚盼诸位学友不吝赐教,一同切磋琢磨,于学海中结伴同行。
- 资料地址:computing-system-security
一 数组
T A[L],表示类型为 T、长度为 L 的数组,在内存中连续分配L * sizeof(T)字节的区域。char string[12]:分配 12 字节int val[5]:分配 20 字节(每个 int 占 4 字节)double a[3]:分配 24 字节(每个 double 占 8 字节)char *p[3]:分配 24 字节(每个指针占 8 字节)
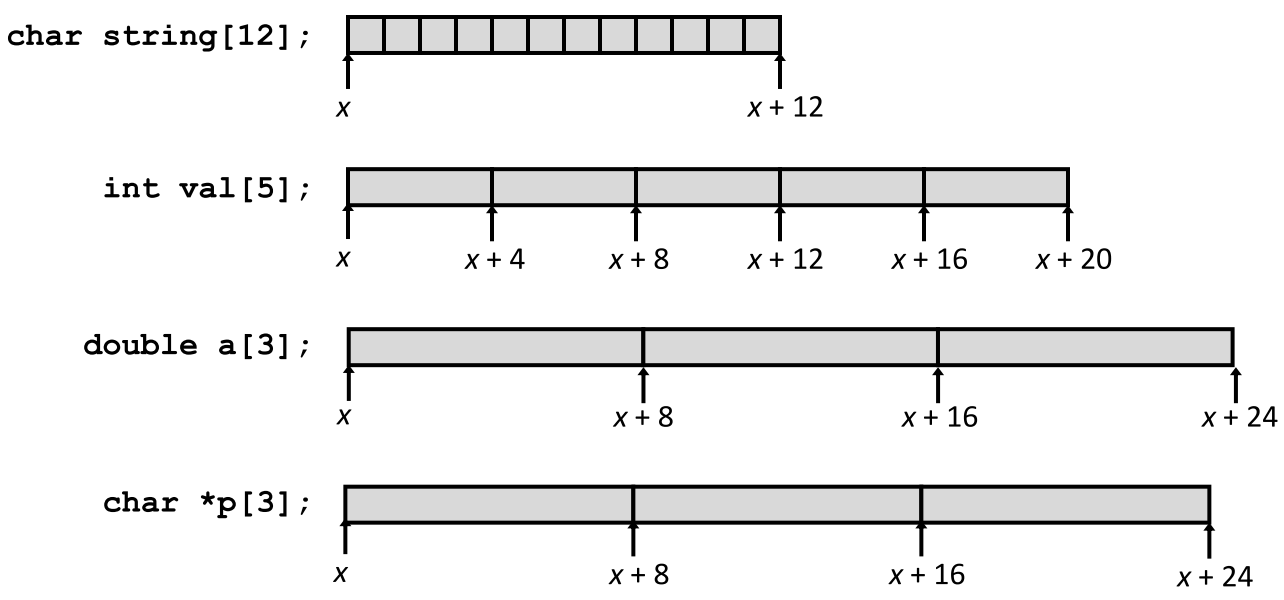
- 标识符 A 可作为指向第 0 个元素的指针,类型为
T*。
| Reference | Type | Value |
|---|---|---|
| val[4] | int | 3 |
| val | int * | x |
| val+1 | int * | x + 4 |
| &val[2] | int * | x + 8 |
| val[5] | int | ?? |
| *(val+1) | int | 5 //val[1] |
| val + i | int * | x + 4 * i //&val[i] |

- 自定义类型
typedef int zip_dig[ZLEN]等价于int cmu[5]。 cmu = {1,5,2,1,3}分配在 20 字节块。mit = {0,2,1,3,9}和ucb = {9,4,7,2,0}连续分配。
1.1 访问数组元素

-
访问数据元素的函数:
cint get_digit (zip_dig z, int digit) { return z[digit]; } -
对应的汇编代码:
python# %rdi = z # %rsi = digit movl (%rdi,%rsi,4), %eax # z[digit] -
%rdi存储数组起始地址。 -
%rsi存储索引值。 -
使用指令
movl (%rdi,%rsi,4), %eax实现z[digit],元素地址计算%rdi + 4 * %rsi。
1.2 数组循环递增
- C语言源代码
c
#define ZLEN 5
void zincr(zip_dig z) {
size_t i;
for (i = 0; i < ZLEN; i++)
z[i]++;
}- 对应的汇编
c
# %rdi = z
movl $0, %eax # i = 0
jmp .L3 # goto middle
.L4: # loop:
addl $1, (%rdi,%rax,4) # z[i]++
addq $1, %rax # i++
.L3: # middle
cmpq $4, %rax # i:4
jbe .L4 # if <=, goto loop
rep; ret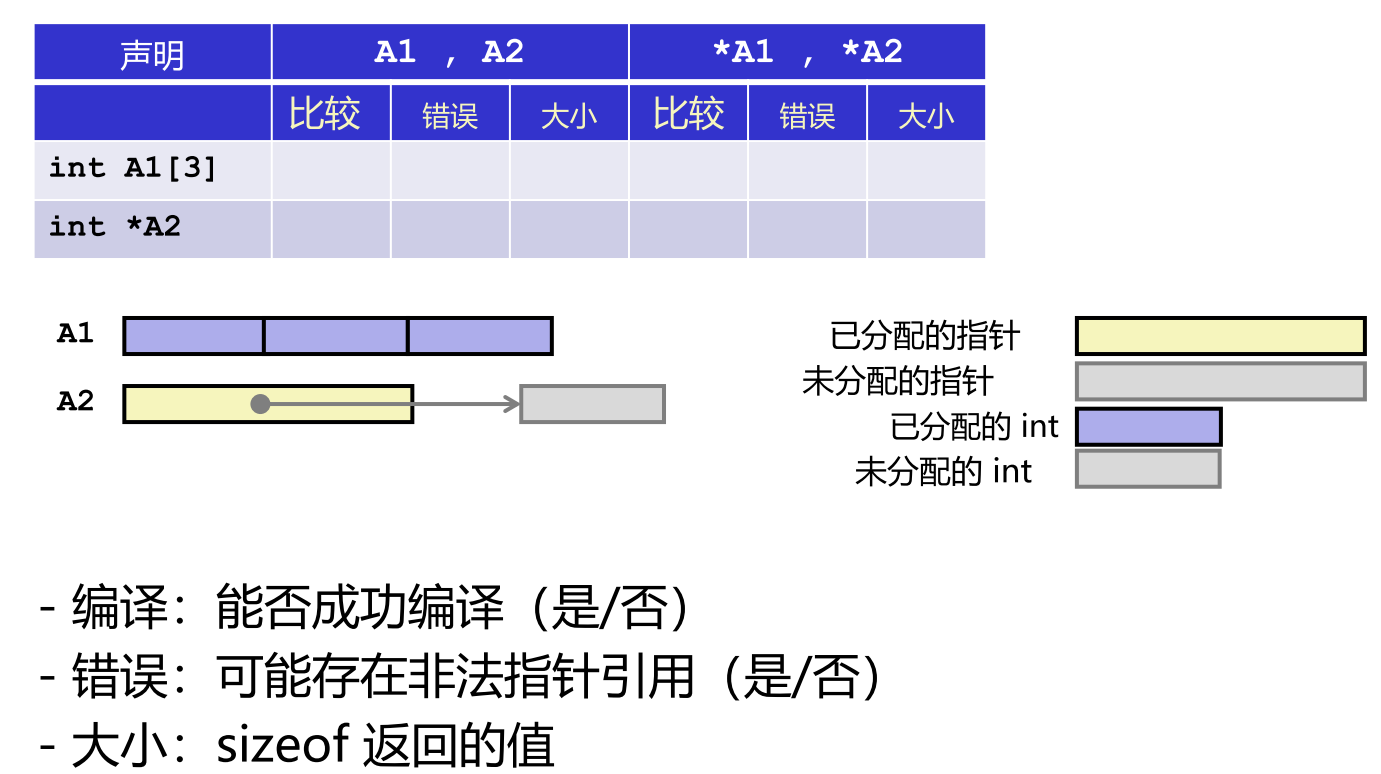
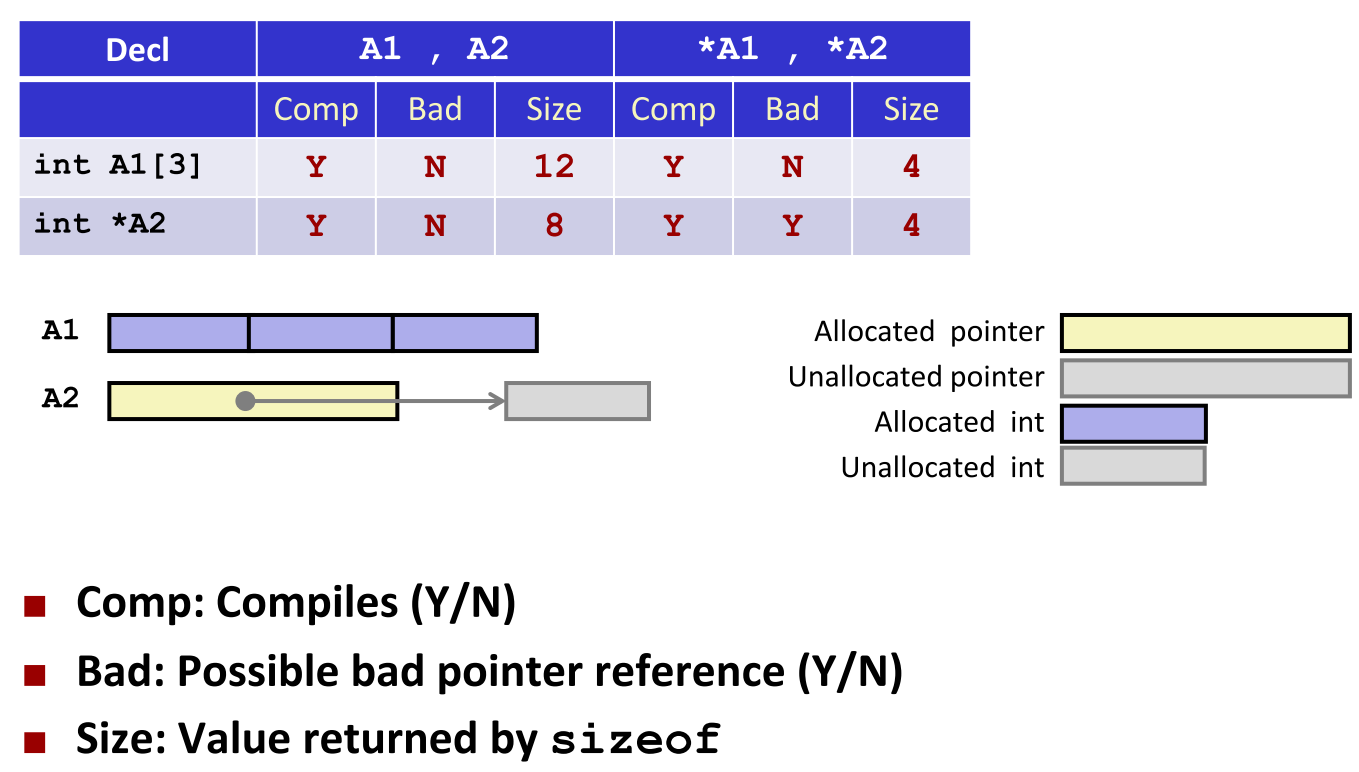
A1:编译成功(是),无非法引用风险(否),sizeof(A1)返回 12(3×4 字节)。*A1:编译成功(是),合法访问首元素(否),sizeof(*A1)返回 4(一个 int 大小)。A2:编译成功(是),无非法引用风险(否),但未初始化,sizeof(A2)返回 8(指针大小)。*A2:编译成功(是),存在非法引用风险(是),因指向未分配内存,sizeof(*A2)返回 4。
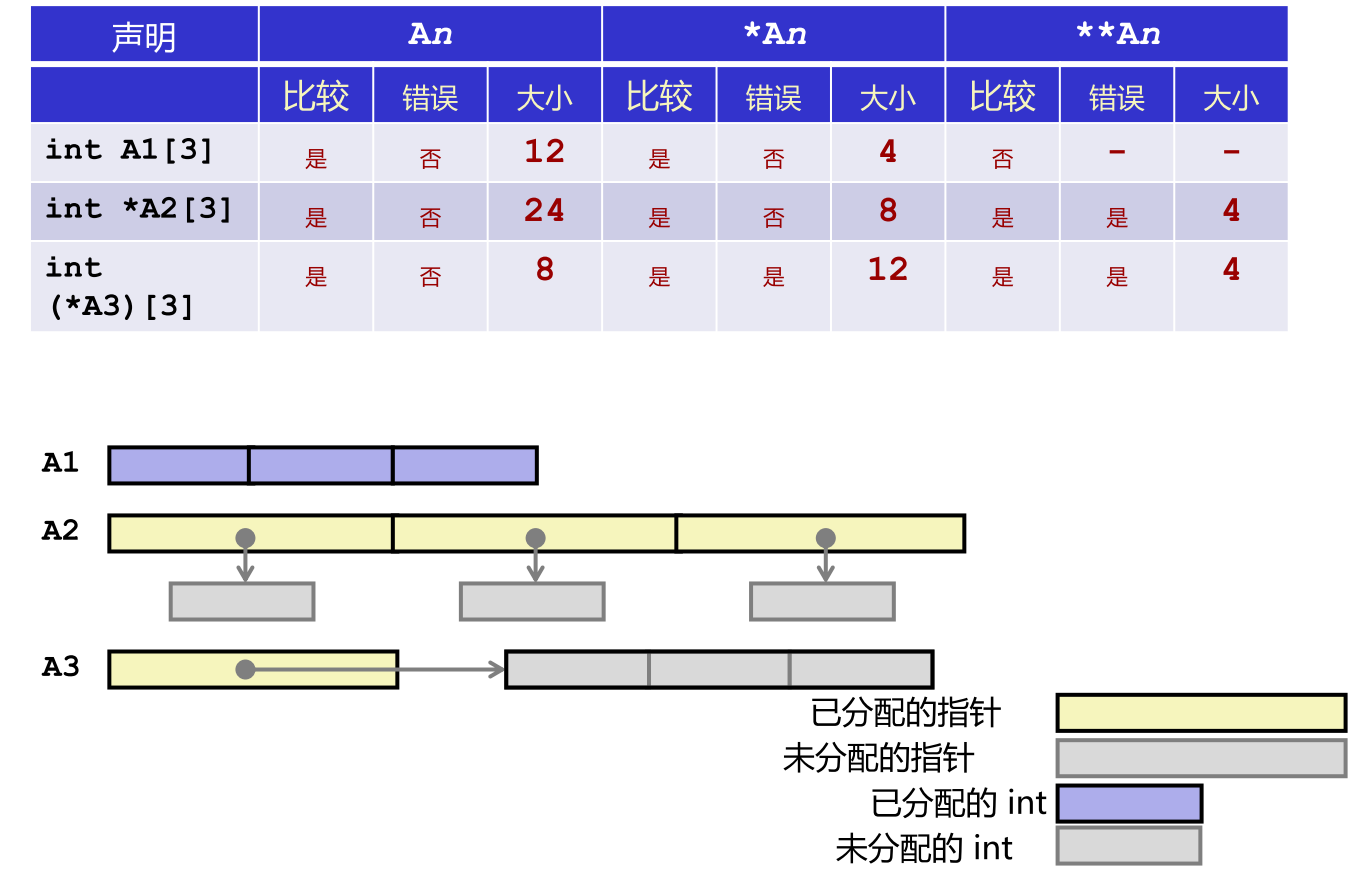
声明 int A1[3]
An(即A1):大小 12,合法*An(即*A1):大小 4,合法**An:不合法(否),无法双重解引用
声明 int *A2[3]
- 含义:包含 3 个 int 指针的数组
An(A2):大小 24(3×8 字节),合法*An(*A2):返回第一个指针,大小 8,合法**An(**A2):解引用得 int,大小 4,但存在非法访问风险
声明 int (*A3)[3]
- 含义:指向包含 3 个 int 的数组的指针
An(A3):大小 8(指针),合法*An(*A3):解引用得整个数组,大小 12,但访问有风险**An(**A3):再解引用得 int,大小 4,有风险
1.3 多层(嵌套)数组
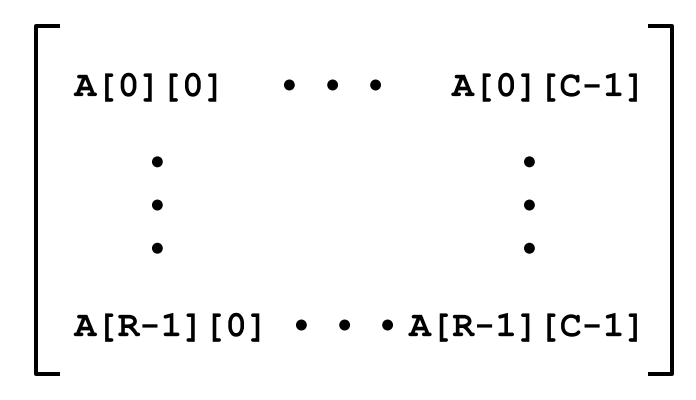
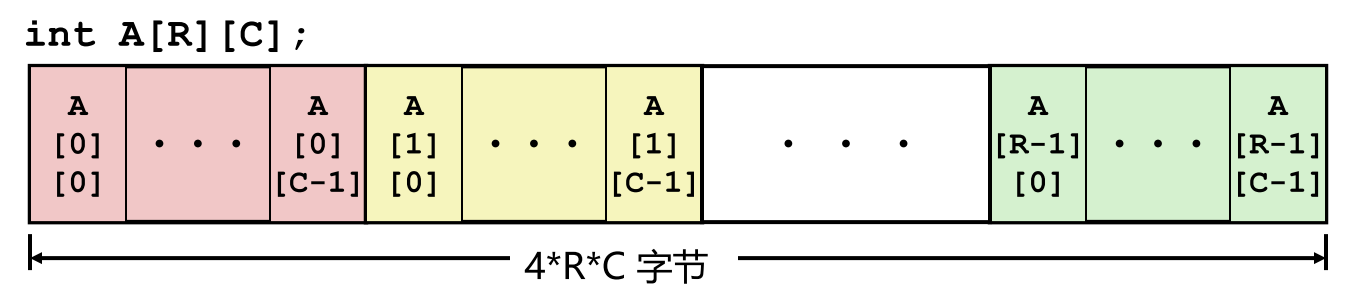
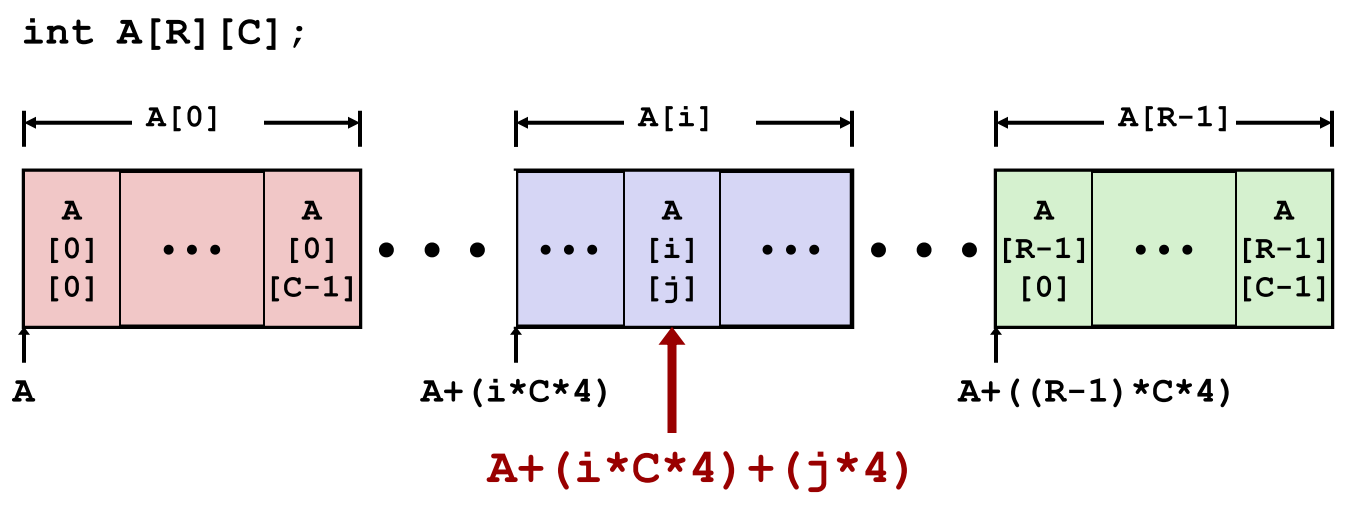
T A[R][C]:表示 R 行 C 列的二维数组。- 总大小:
R * C * sizeof(T)字节 - 内存布局采用行优先顺序(Row-Major Ordering),示例:
int A[R][C]中元素按行依次存储。
python
#define PCOUNT 4
typedef int zip_dig[5];
zip_dig pgh[PCOUNT] =
{{1, 5, 2, 0, 6},
{1, 5, 2, 1, 3 },
{1, 5, 2, 1, 7 },
{1, 5, 2, 2, 1 }};
- 定义:
zip_dig pgh[PCOUNT]等价于int pgh[4][5]。 - 数据内容:四个 ZIP 码:{1,5,2,0,6}、{1,5,2,1,3} 等。
- 内存分配特点:整体连续分配,共 80 字节(4×5×4),每个子数组(每行)连续存放。
- 所有元素按行优先排列。
1.3.1 行向量访问
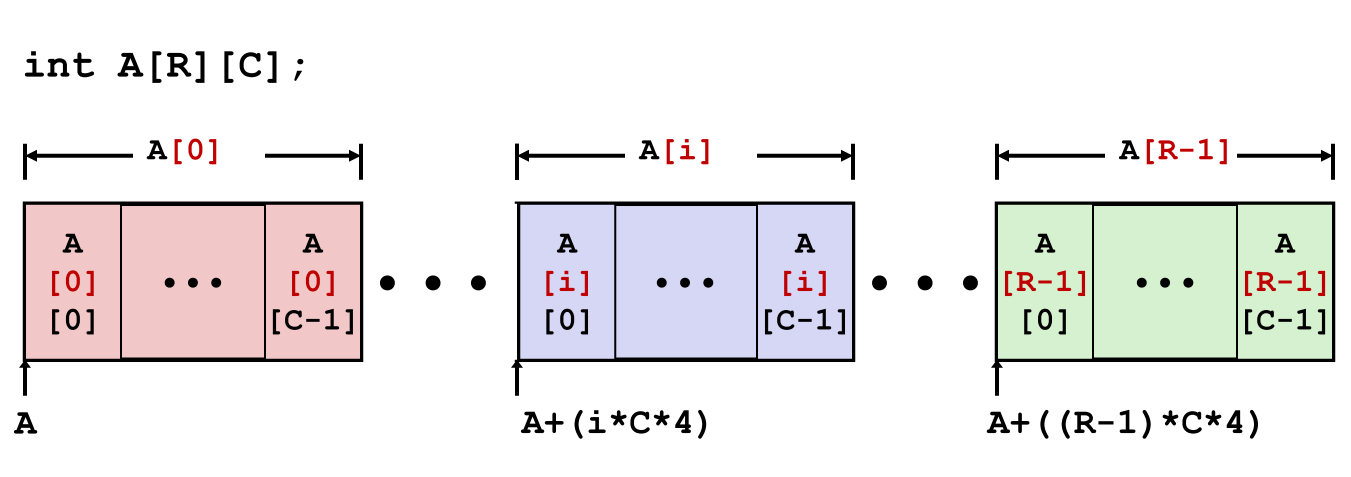
行访问机制
A[i]表示第 i 行,是一个包含 C 个 T 类型元素的数组。- 起始地址计算公式:
A + i * (C * sizeof(T))。 - 示例:
pgh[index]起始地址为pgh + 20 * index。
- 汇编实现

leaq (%rdi,%rdi,4), %rax→ 计算5 * index((%rdi,%rdi,4)等同于 rdi + rdi*4)leaq pgh(,%rax,4), %rax→ 计算pgh + 20 * index( p g h + r a x ∗ 4 = p g h + ( 5 ∗ i n d e x ) ∗ 4 = p g h + 20 ∗ i n d e x pgh + rax*4 = pgh + (5*index)*4 = pgh + 20*index pgh+rax∗4=pgh+(5∗index)∗4=pgh+20∗index)
1.3.2 嵌套数组元素访问
- A [ i ] [ j ] A[i][j] A[i][j]是类型为 T T T 的元素,占用 K K K字节
- 地址计算公式: A + i ∗ ( C ∗ K ) + j ∗ K = A + ( i ∗ C + j ) ∗ K A + i * (C * K) + j * K = A + (i * C + j) * K A+i∗(C∗K)+j∗K=A+(i∗C+j)∗K
- 对于 i n t A [ R ] [ C ] int A[R][C] intA[R][C],每个元素占 4 字节。
c
leaq (%rdi,%rdi,4), %rax # 5*index
addl %rax, %rsi # 5*index+dig
movl pgh(,%rsi,4), %eax # M[pgh + 4*(5*index+dig)]1.4 多级数组表示
c
zip_dig cmu = { 1, 5, 2, 1, 3 };
zip_dig mit = { 0, 2, 1, 3, 9 };
zip_dig ucb = { 9, 4, 7, 2, 0 };
#define UCOUNT 3
int *univ[UCOUNT] = {mit, cmu, ucb};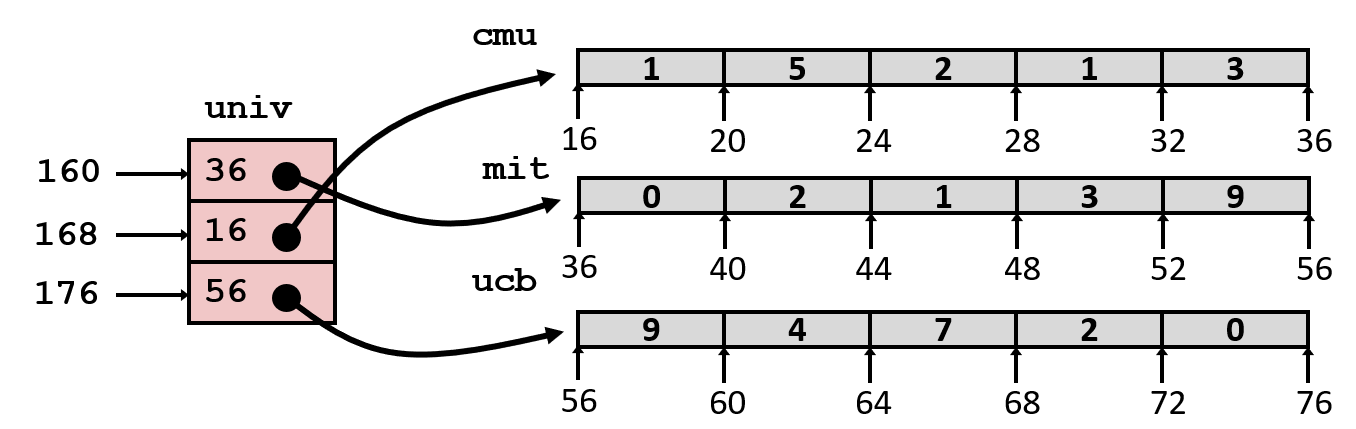
c
int get_univ_digit (size_t index, size_t digit)
{
return univ[index][digit];
}
c
salq $2, %rsi # 4*digit
addq univ(,%rdi,8), %rsi # p = univ[index] + 4*digit
movl (%rsi), %eax # return *p
ret - $salq 2 , 2, %rsi 2,: d i g i t < < 2 = d i g i t ∗ 4 digit << 2 = digit * 4 digit<<2=digit∗4。
- a d d q u n i v ( , addq univ(,%rdi,8), %rsi addquniv(,: u n i v + 8 ∗ i n d e x + 4 ∗ d i g i t univ + 8*index + 4*digit univ+8∗index+4∗digit。
1.5 数组元素访问对比
 地址计算差异
地址计算差异
- 嵌套数组: M e m [ p g h + 20 ∗ i n d e x + 4 ∗ d i g i t ] Mem[pgh+20*index+4*digit] Mem[pgh+20∗index+4∗digit](单次计算,无间接寻址)
- 多级数组: M e m [ M e m [ u n i v + 8 ∗ i n d e x ] + 4 ∗ d i g i t ] Mem[Mem[univ+8*index]+4*digit] Mem[Mem[univ+8∗index]+4∗digit](双重内存访问,需先取指针)
二 结构体(重点)
bash
# r in %rdi, idx in %rsi
leaq (%rdi,%rsi,4), %rax
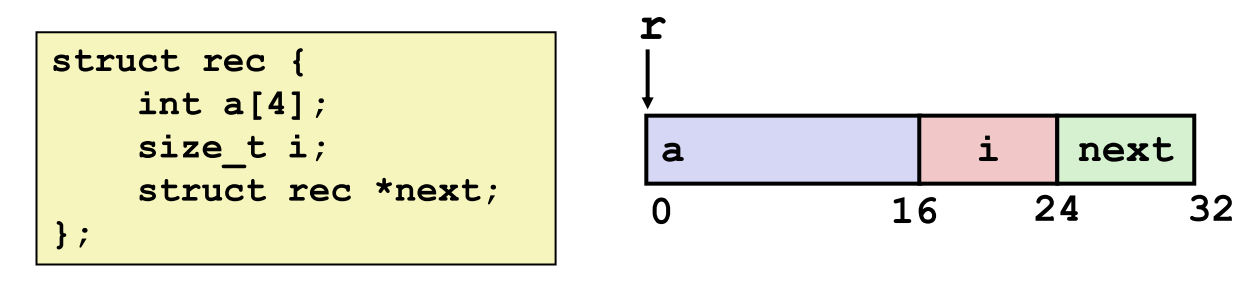
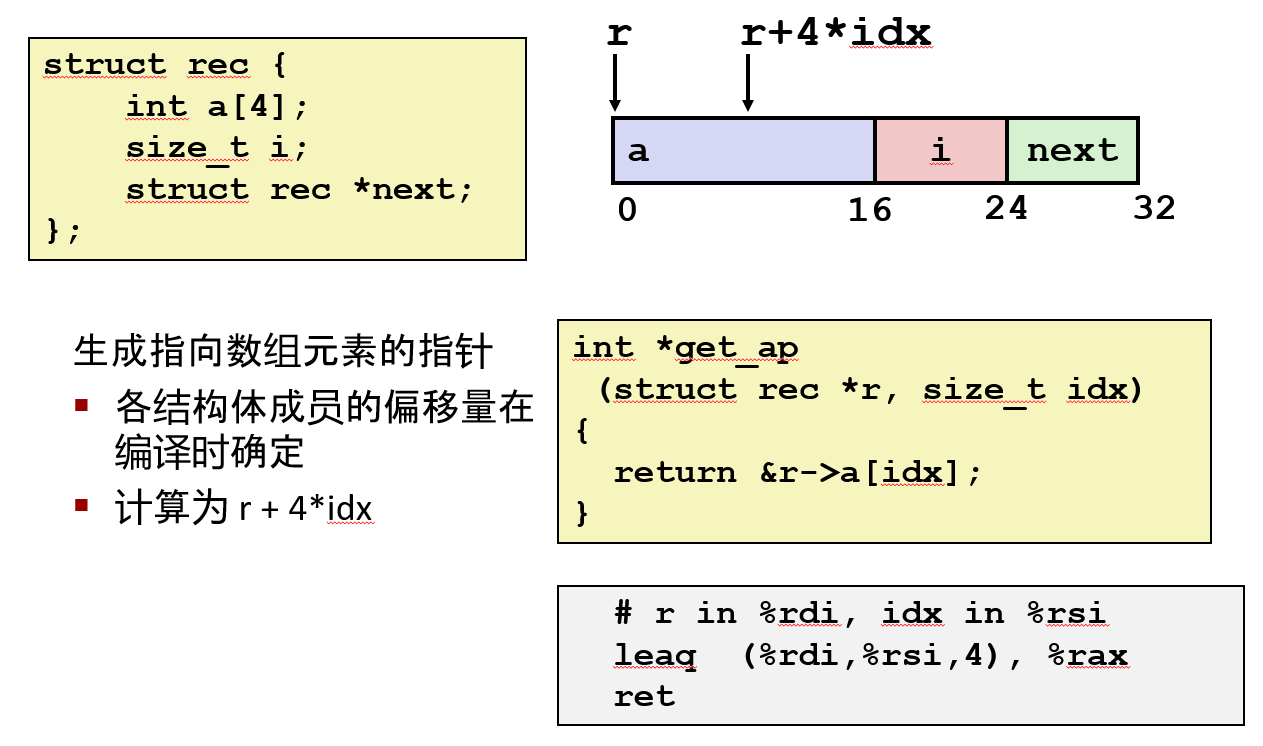
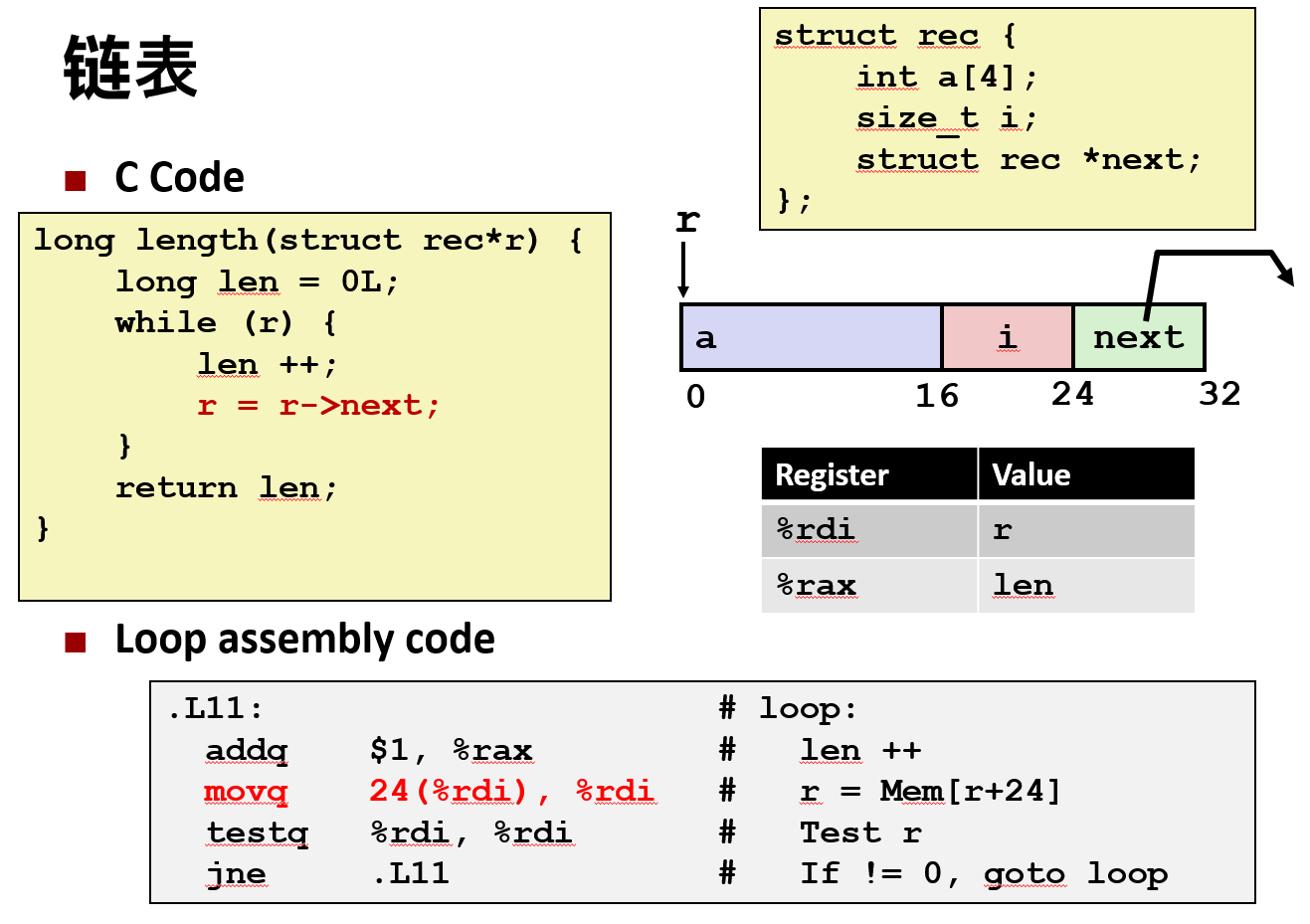
ret- a 数组从偏移0开始,占用16字节(4个int,每个4字节)
- i 从偏移16开始,占用8字节
- next 指针从偏移24开始,占用8字节
存储特性
- 结构体以连续内存块表示,一块的大小需要保证容纳所有字段。
- 字段按声明顺序排列,即使采用其他字段排列顺序可能因对齐规则(即将介绍)而获得更紧凑的表示。
- 编译器决定整体大小和字段位置,机器代码不识别结构体语义。
- %rdi(64位)→ %edi(低32位)→ %dil(低8位)
- %rax(64位)→ %eax(低32位)→ %al(低8位)
- %rbx(64位)→ %ebx(低32位)→ %bl(低8位)
2.1 结构体内存对齐规则
| 规则类型 | 说明 | 示例 |
|---|---|---|
| 基本对齐 | 每个成员按其自身大小对齐 | int按4字节对齐 |
| 结构体对齐 | 整个结构体按最大成员大小对齐 | 含double的结构体按8字节对齐 |
| 数组对齐 | 数组按元素类型对齐 | int数组按4字节对齐 |
| 嵌套结构体 | 按内部结构体的最大成员对齐 | 嵌套结构体按其内部最大成员对齐 |
- C语言常用数据类型字节占用表。
| 数据类型 | 32位系统 | 64位系统 | 说明 |
|---|---|---|---|
| 基本整型 | |||
| char | 1 | 1 | 字符型 |
| signed char | 1 | 1 | 有符号字符 |
| unsigned char | 1 | 1 | 无符号字符 |
| short | 2 | 2 | 短整型 |
| unsigned short | 2 | 2 | 无符号短整型 |
| int | 4 | 4 | 整型 |
| unsigned int | 4 | 4 | 无符号整型 |
| long | 4 | 8 | 长整型 |
| unsigned long | 4 | 8 | 无符号长整型 |
| long long | 8 | 8 | 长长整型 |
| unsigned long long | 8 | 8 | 无符号长长整型 |
| 浮点型 | |||
| float | 4 | 4 | 单精度浮点 |
| double | 8 | 8 | 双精度浮点 |
| long double | 8/12/16 | 16 | 长双精度(依赖编译器) |
| 指针类型 | |||
| void* | 4 | 8 | 任意类型指针 |
| int* | 4 | 8 | 整型指针 |
| char* | 4 | 8 | 字符指针 |
| 其他类型 | |||
| bool | 1 | 1 | 布尔型(C99) |
| size_t | 4 | 8 | sizeof返回类型 |
c
#include <stdio.h>
// 示例1:简单结构体
struct Example1 {
char a; // 1字节
int b; // 4字节,需要3字节填充
char c; // 1字节
// 总共:1 + 3(填充) + 4 + 1 + 3(填充) = 12字节
};
// 示例2:优化后的结构体
struct Example2 {
int b; // 4字节
char a; // 1字节
char c; // 1字节
// 总共:4 + 1 + 1 + 2(填充) = 8字节
};
// 示例3:含指针的结构体
struct Example3 {
int value; // 4字节
char* ptr; // 32位:4字节,64位:8字节
double d; // 8字节
// 32位:4 + 4 + 8 = 16字节
// 64位:4 + 4(填充) + 8 + 8 = 24字节
};2.2 内存对齐:为何重要?
性能考量
- 提升访存效率:CPU 按 4/8 字节块读取数据,对齐可减少内存访问周期。
- 避免缓存行分割:防止单个数据横跨 64 字节缓存行,避免额外的内存访问和延迟。
- 遵循硬件建议:如 Intel 架构建议避免数据跨越 16 字节边界,以优化指令执行。
简化系统设计
- 规避跨页问题:确保数据不落在两个 4KB 虚拟内存页上,简化内存管理单元(MMU)的处理逻辑。
编译器的智能处理
- 自动填充(Padding):编译器会在结构体成员间自动插入填充字节,确保每个成员都满足其对齐要求。
- 保证对齐:最终结构体的整体大小也会是其最宽成员对齐值的整数倍,保证在数组中也能正确对齐。
2.3 通过结构体实现对齐
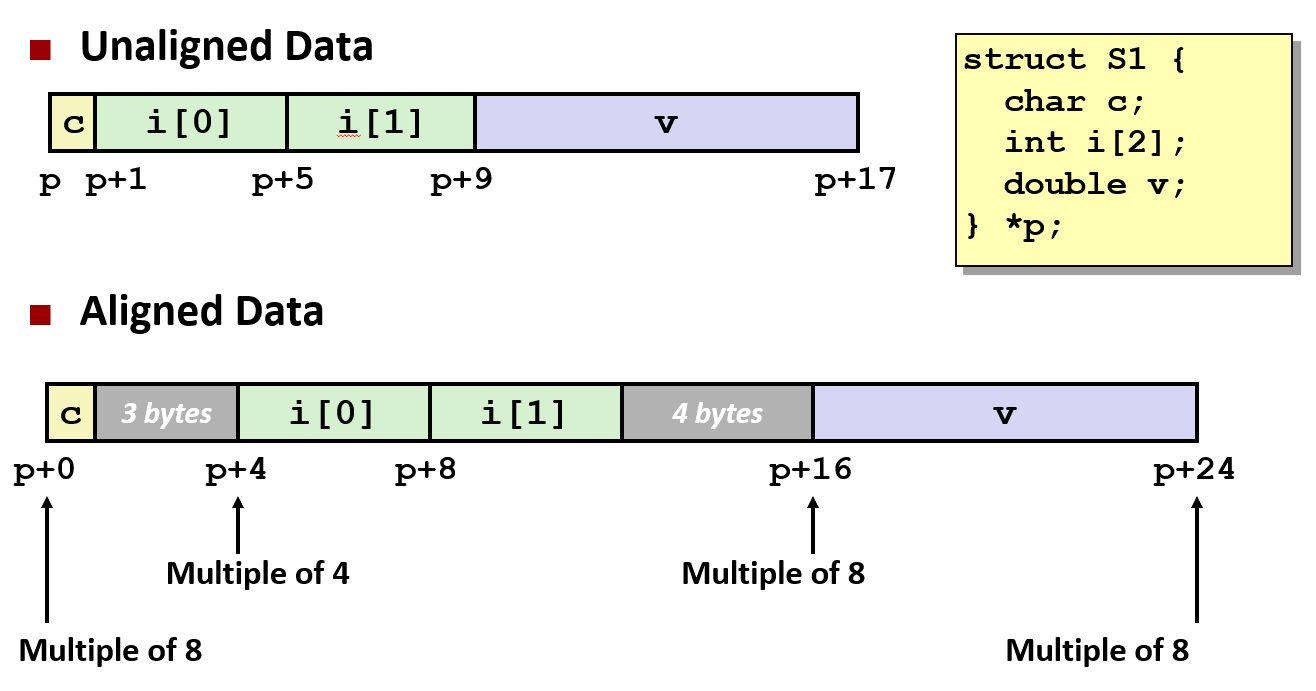
一个 N 字节类型的数据,其内存起始地址必须是 N 的倍数。
- 2 字节类型 (short):地址必须是 2 的倍数,即二进制表示的最低位为 0(偶数地址)。
- 4 字节类型 (int, float) :地址必须是 4 的倍数,即二进制表示的最低 2 位为
00。 - 8 字节类型 (double, long, 指针) :地址必须是 8 的倍数,即二进制表示的最低 3 位为
000。
结构体内对齐策略
- 单个元素对齐:每个成员按自身大小对齐
整体结构对齐要求 K
- K = 结构体中最大成员的对齐要求
- 示例:struct S1 中因 double v 存在,K = 8
地址与长度约束
- 起始地址必须是 K 的倍数
- 结构体总长度也必须是 K 的倍数
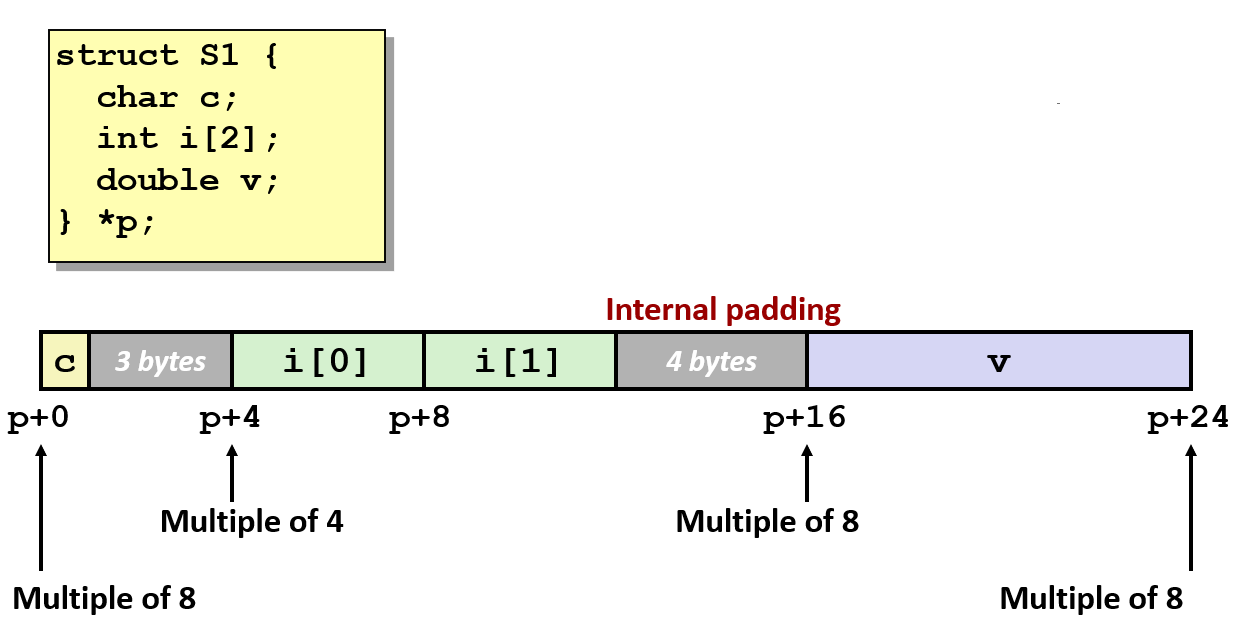
内部填充
- 在 char c 后添加 3 字节填充,使 int i[2] 对齐到 4 字节边界
- 总大小由 17 字节扩展至 24 字节(8 的倍数)
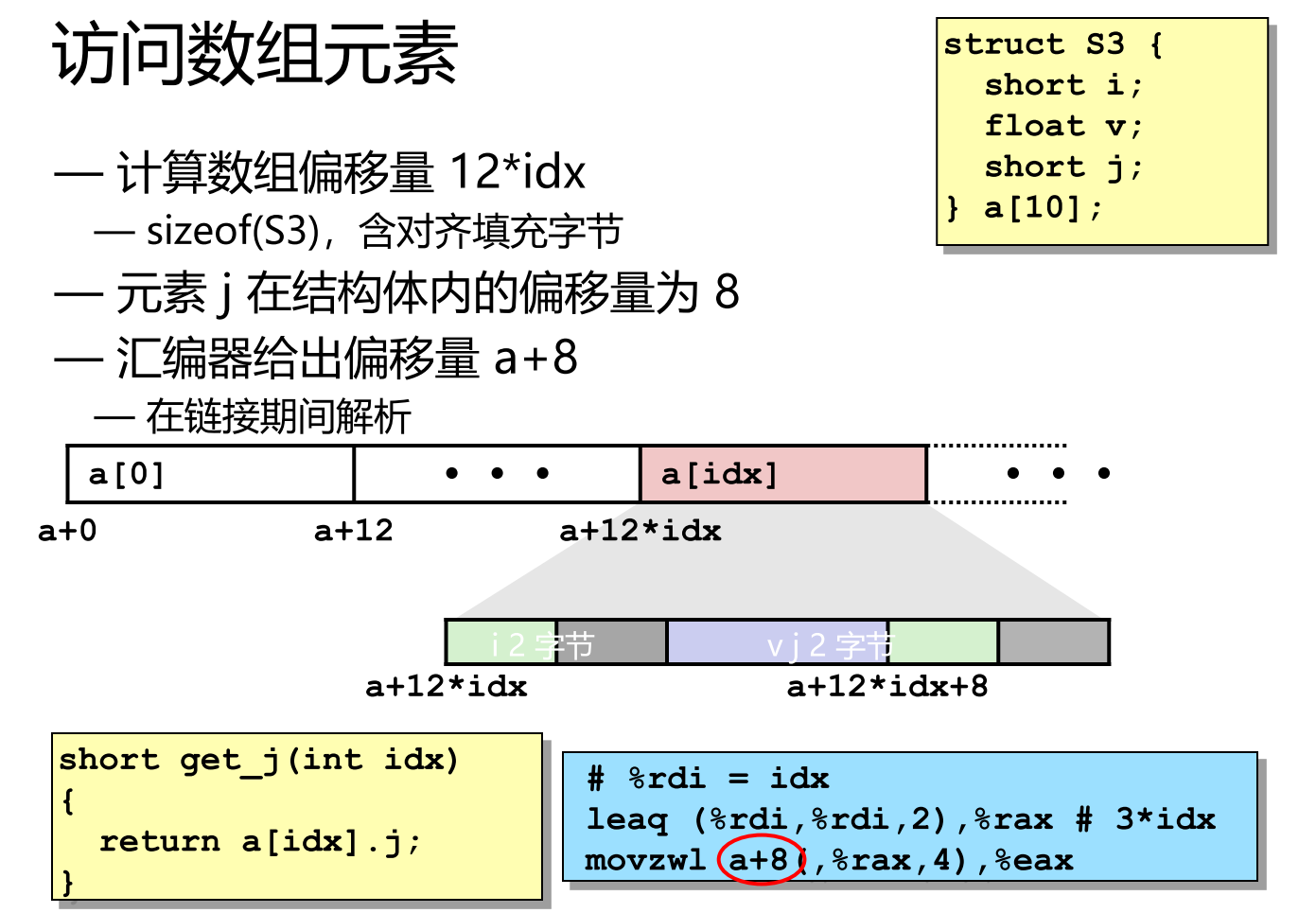
2.4 结构体数组和元素访问
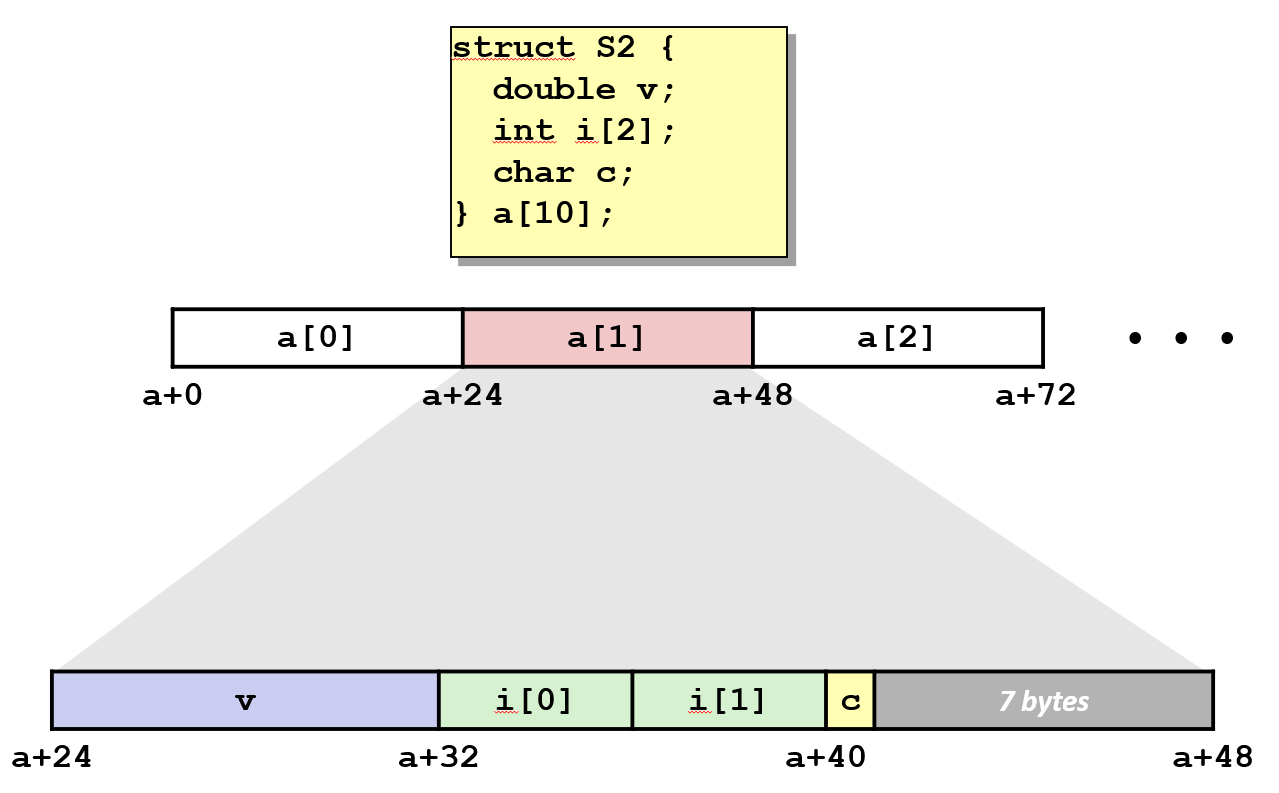
- 单个结构体对齐占用分析。
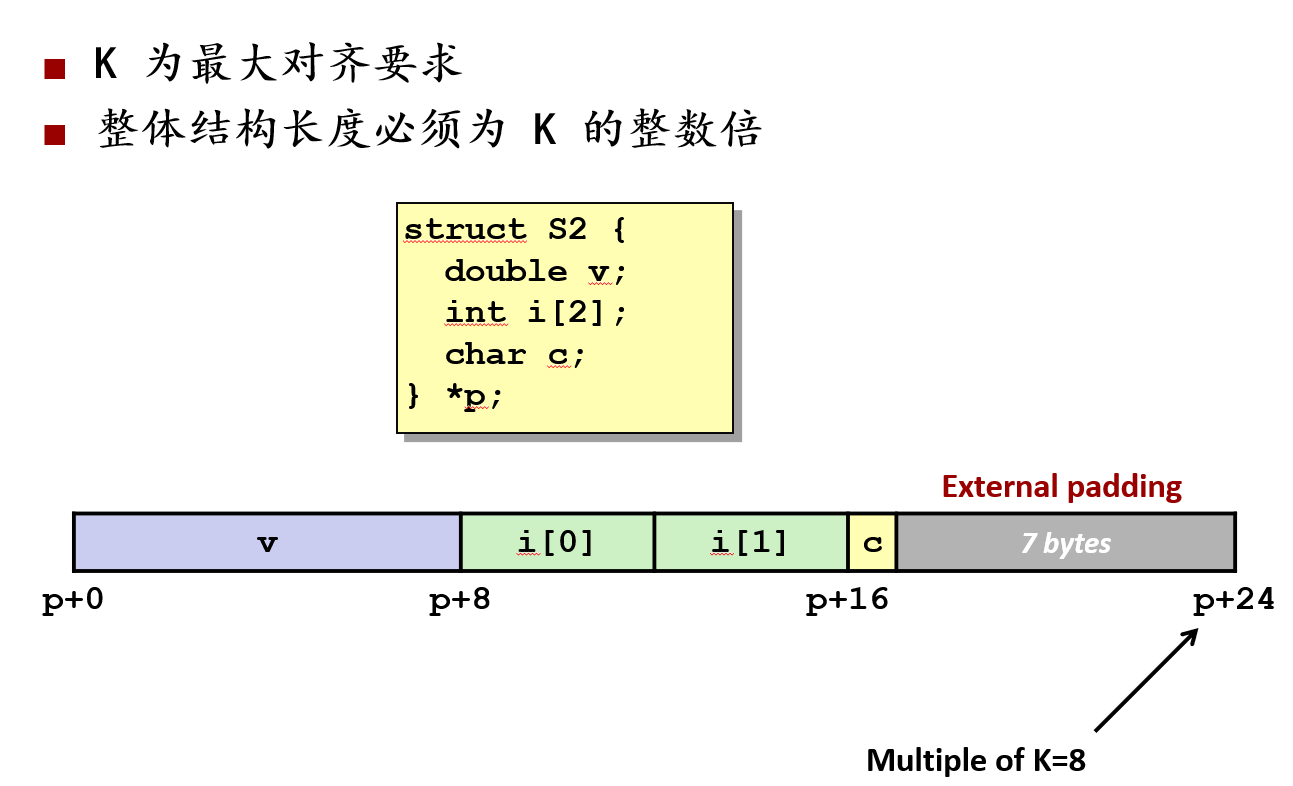
- 成员顺序:double v(8B)、int i[2](8B)、char c(1B),K = 8,因此整体长度需为 8 的倍数。
- 每个结构体实例起始地址均为单个结构体的倍数。数组连续存放,步长等于对齐后结构体大小(如 24 字节)。
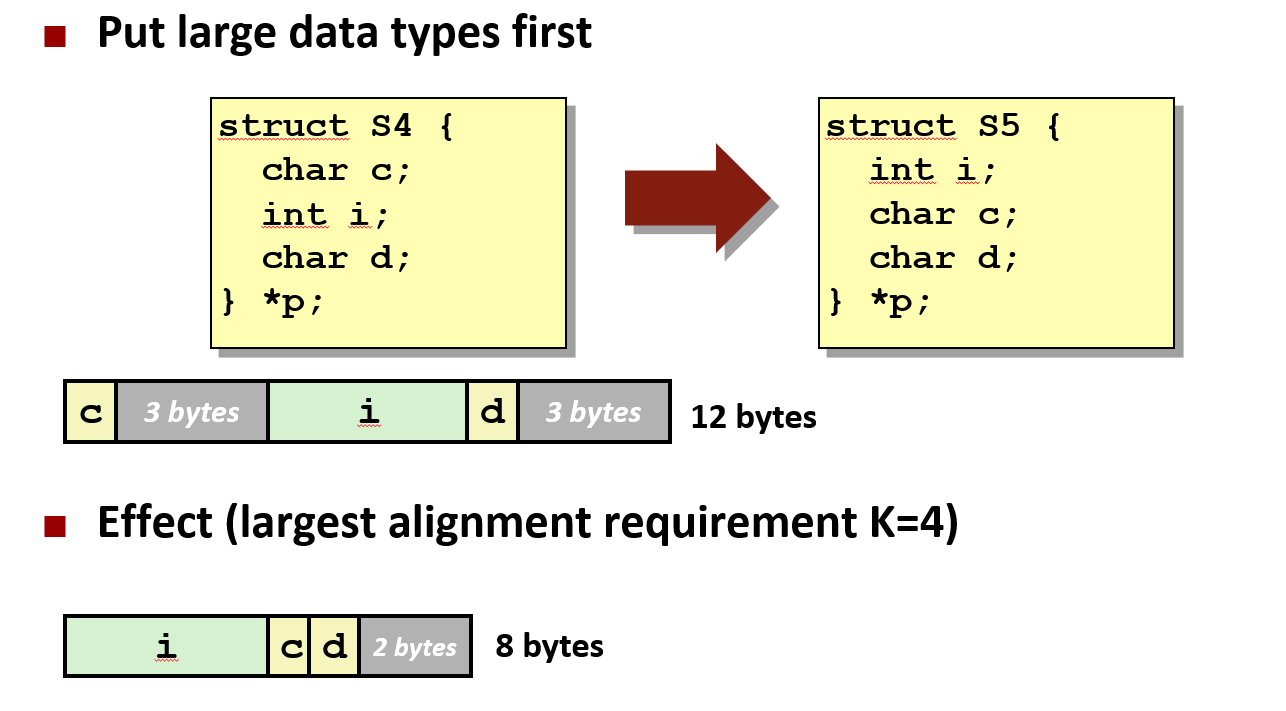
2.5 成员排序优化
2.6 结构体对齐考试题(重点)
c
typedef struct {
char a;
long b; # long 类型 8 字节
float c; # float 类型 4 字节
char d[3];
int *e; # int * 类型 8 字节
short *f; # short * 类型 8 字节
} foo;- 展示 foo 在 x86-64 Linux 系统上的内存分配方式。用不同字段的名称标注字节,并清晰地标明结构体的结束。用 X 表示结构体中作为填充分配的空间。
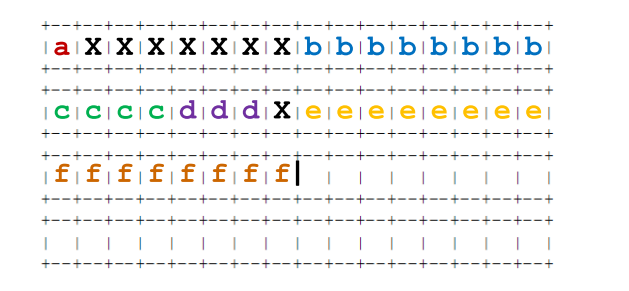
- 调整 foo 的元素顺序以最大程度节省内存空间。用不同字段的名称标注字节,并清晰地标明结构体的结束。用 X 表示结构体中作为填充分配的空间。