永磁同步电机,基于扩展卡尔曼滤波算法无传感器仿真模型,s函数编写算法,基于matlab/simulink搭建。
在电机控制领域,永磁同步电机(PMSM)因其高效、节能等优点被广泛应用。而无传感器控制技术能省去传感器,降低成本、提高系统可靠性,其中扩展卡尔曼滤波(EKF)算法是常用手段。今天就来聊聊如何基于Matlab/Simulink搭建基于扩展卡尔曼滤波算法的永磁同步电机无传感器仿真模型,以及关键的S函数编写。
永磁同步电机基础原理
永磁同步电机通过定子绕组产生旋转磁场,与转子永磁体相互作用实现能量转换。其数学模型在dq坐标系下可表示为:
\[
\begin{cases}
ud = R sid + L d\frac{did}{dt} - \omega eLqiq \\
uq = R siq + L q\frac{diq}{dt} + \omega e(Ldid + \psi_f)
\end{cases}
\]
这里 \( ud, u q \) 是dq轴电压, \( id, i q \) 是dq轴电流, \( Rs \) 是定子电阻, \( L d, Lq \) 是dq轴电感, \( \omegae \) 是电角速度, \( \psi_f \) 是永磁体磁链。
扩展卡尔曼滤波算法
扩展卡尔曼滤波用于估计系统状态,能处理非线性系统。其核心步骤包括预测和更新。
预测阶段:
\[
\begin{cases}
\hat{x}{k|k - 1} = f(\hat{x}{k - 1|k - 1}, u_{k - 1}) \\
P*{k|k - 1} = F* {k - 1}P*{k - 1|k - 1}F*{k - 1}^T + Q_{k - 1}
\end{cases}
\]
更新阶段:
\[
\begin{cases}
Kk = P {k|k - 1}Hk^T(H kP*{k|k - 1}H*k^T + R_k)^{-1} \\
\hat{x}{k|k} = \hat{x} {k|k - 1} + Kk(zk - h(\hat{x}_{k|k - 1})) \\
P*{k|k} = (I - K* kHk)P{k|k - 1}
\end{cases}
\]
其中 \( \hat{x} \) 是状态估计值, \( P \) 是估计误差协方差, \( F \) 是状态转移矩阵, \( Q \) 是过程噪声协方差, \( H \) 是观测矩阵, \( R \) 是观测噪声协方差, \( z \) 是观测值。
S函数编写算法
在Matlab中,S函数是自定义模块的有力工具。以下是一个简单的基于EKF算法估计PMSM转速和位置的S函数框架(以Matlab语言为例):
matlab
function [sys,x0,str,ts] = ekf_sfun(t,x,u,flag)
% 初始化
switch flag,
case 0,
[sys,x0,str,ts]=mdlInitializeSizes;
case 1,
sys=mdlDerivatives(t,x,u);
case 2,
sys=mdlUpdate(t,x,u);
case 3,
sys=mdlOutputs(t,x,u);
case 4,
sys=mdlGetTimeOfNextVarHit(t,x,u);
case 9,
sys=mdlTerminate(t,x,u);
otherwise
DAStudio.error('Simulink:blocks:unhandledFlag', num2str(flag));
end
function [sys,x0,str,ts]=mdlInitializeSizes
sizes = simsizes;
sizes.NumContStates = 0;
sizes.NumDiscStates = 2; % 假设估计转速和位置两个状态
sizes.NumOutputs = 2;
sizes.NumInputs = 4; % 例如输入电流、电压等信息
sizes.DirFeedthrough = 1;
sizes.NumSampleTimes = 1;
sys = simsizes(sizes);
x0 = [0;0]; % 初始估计值
str = [];
ts = [0.001 0]; % 采样时间
function sys=mdlDerivatives(t,x,u)
sys = [];
function sys=mdlUpdate(t,x,u)
% 这里进行EKF预测和更新步骤的具体实现
% 例如更新状态估计值x
% 计算过程噪声等
sys = [新的转速估计值;新的位置估计值];
function sys=mdlOutputs(t,x,u)
sys = x; % 输出估计的转速和位置
function sys=mdlGetTimeOfNextVarHit(t,x,u)
sampleTime = 0.001;
sys = t + sampleTime;
function sys=mdlTerminate(t,x,u)
sys = [];在上述代码中,mdlInitializeSizes函数设置了S函数的基本属性,如输入输出端口数量、状态变量数量等。mdlUpdate函数则是核心的EKF算法实现处,在实际应用中需要根据PMSM的具体模型和EKF算法公式填充具体计算代码。
基于Matlab/Simulink搭建仿真模型
打开Matlab的Simulink,首先搭建PMSM的模型,可利用Simscape Electrical库中的永磁同步电机模块,设置好电机参数。
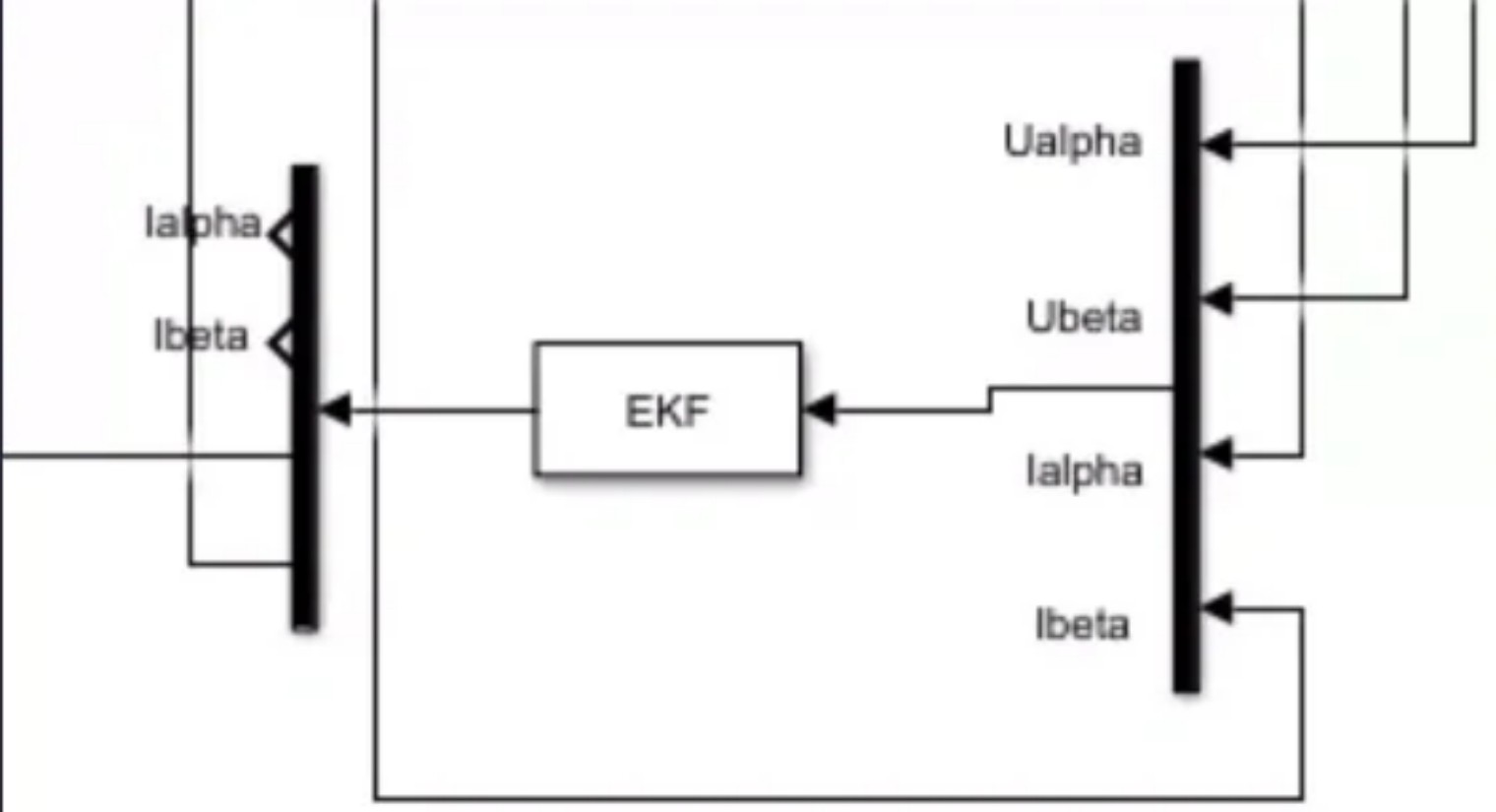
然后,将编写好的S函数模块拖入模型中,连接好输入输出端口。输入端口连接PMSM的电流、电压等可测量信号,输出端口连接到转速和位置观测的显示模块。
再搭建控制系统部分,如采用矢量控制策略,通过坐标变换、PI调节器等模块实现对PMSM的有效控制。
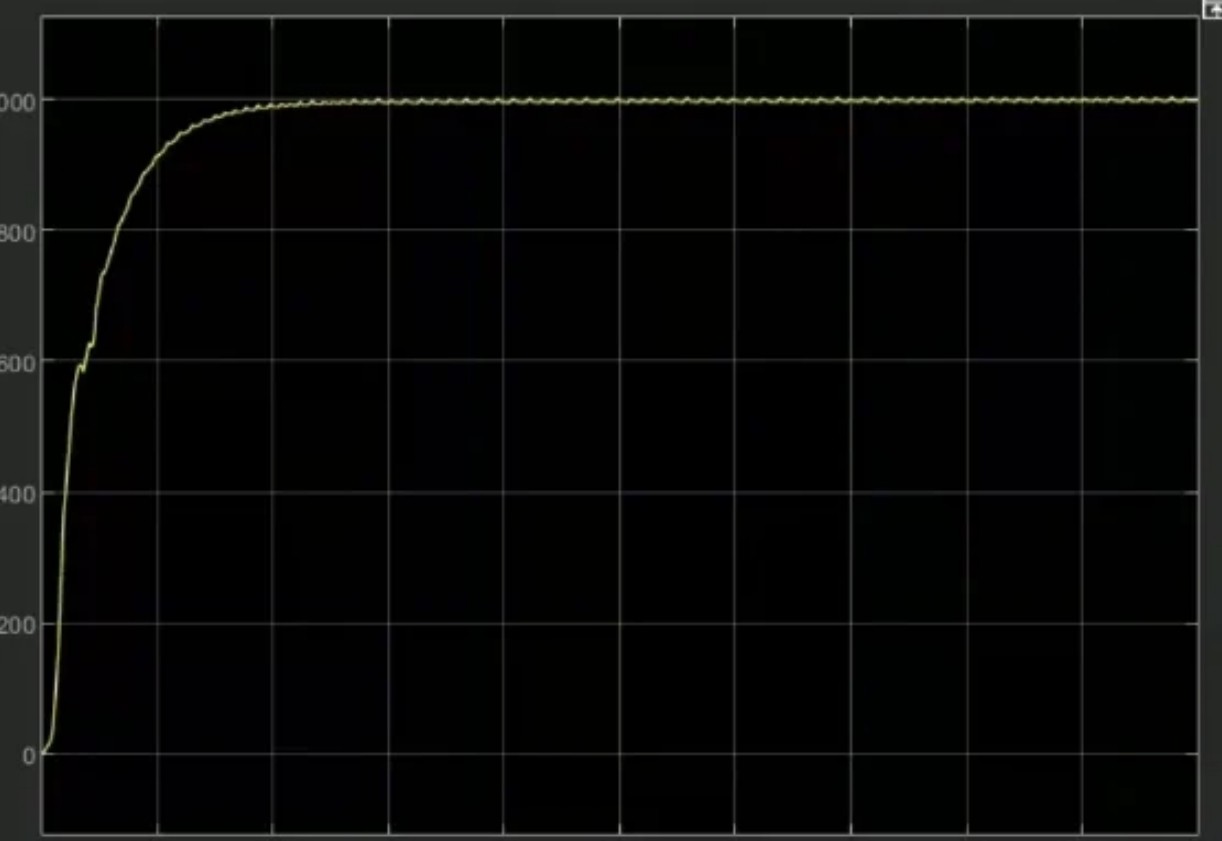
完成搭建后,设置好仿真参数,如仿真时间、步长等,运行仿真。从结果中可以观察到基于扩展卡尔曼滤波算法的无传感器控制下,PMSM转速和位置的估计精度,以及系统的动态响应性能。
通过这样一步步的搭建,我们就能实现永磁同步电机基于扩展卡尔曼滤波算法无传感器的仿真研究,为实际应用提供理论支持和验证。希望这篇博文能给对这方面感兴趣的朋友一些启发和帮助。