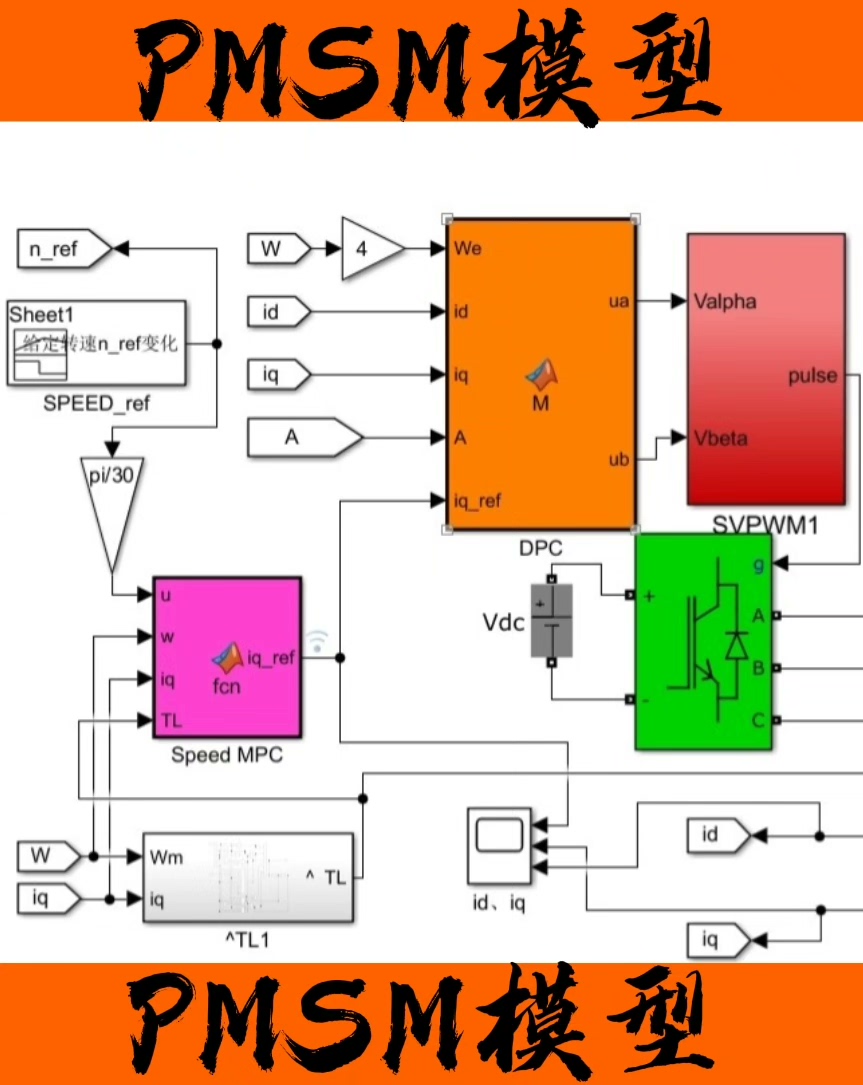
基于扰动观测器的永磁同步电机（PMSM）模型预测控制（MPC）仿真探索

基于扰动观测器的永磁同步电机（PMSM）模型预测控制（MPC）仿真速度外环基于模型预测控制、电流内环基于无差拍控制搭建，控制效果理想，模块程序设计通俗易通

在电机控制领域，永磁同步电机（PMSM）因其高效、节能等优点被广泛应用。而如何实现对PMSM更精准、高效的控制一直是研究的热点。今天就来聊聊基于扰动观测器的PMSM模型预测控制（MPC）仿真相关内容。

这次的控制策略中，速度外环基于模型预测控制，电流内环基于无差拍控制搭建，实际效果还挺理想，而且模块程序设计通俗易懂，这对于我们深入理解和实践都很友好。

速度外环 - 模型预测控制（MPC）

模型预测控制是一种基于模型的先进控制策略，它通过预测系统未来的行为，并根据优化目标来计算当前的控制输入。

简单说，在速度外环MPC里，我们首先要建立PMSM的离散时间模型。比如，假设我们已经有了如下离散时间状态方程：

python 复制代码

# 这里以Python代码简单示意状态方程离散化，实际可能会结合电机参数在其他环境下更严谨推导
A = np.array([[1, Ts], [0, 1 - B * Ts / J]])
B = np.array([[0], [Kt * Ts / J]])

这里A和B就是离散化后的状态矩阵和输入矩阵，Ts是采样时间，J是转动惯量，B是粘滞摩擦系数，Kt是转矩系数。

接下来就是预测环节，我们要预测未来几个时刻的速度：

python 复制代码

# 预测未来N个时刻的速度
def predict_speed(x, u, A, B, N):
    x_pred = np.zeros((2, N))
    x_pred[:, 0] = x
    for k in range(1, N):
        x_pred[:, k] = A @ x_pred[:, k - 1] + B @ u
    return x_pred

这里x是当前状态，u是控制输入。通过这个函数，我们就可以预测出未来N个时刻的速度。然后根据预测结果和目标值，通过优化算法来计算当前的控制输入。

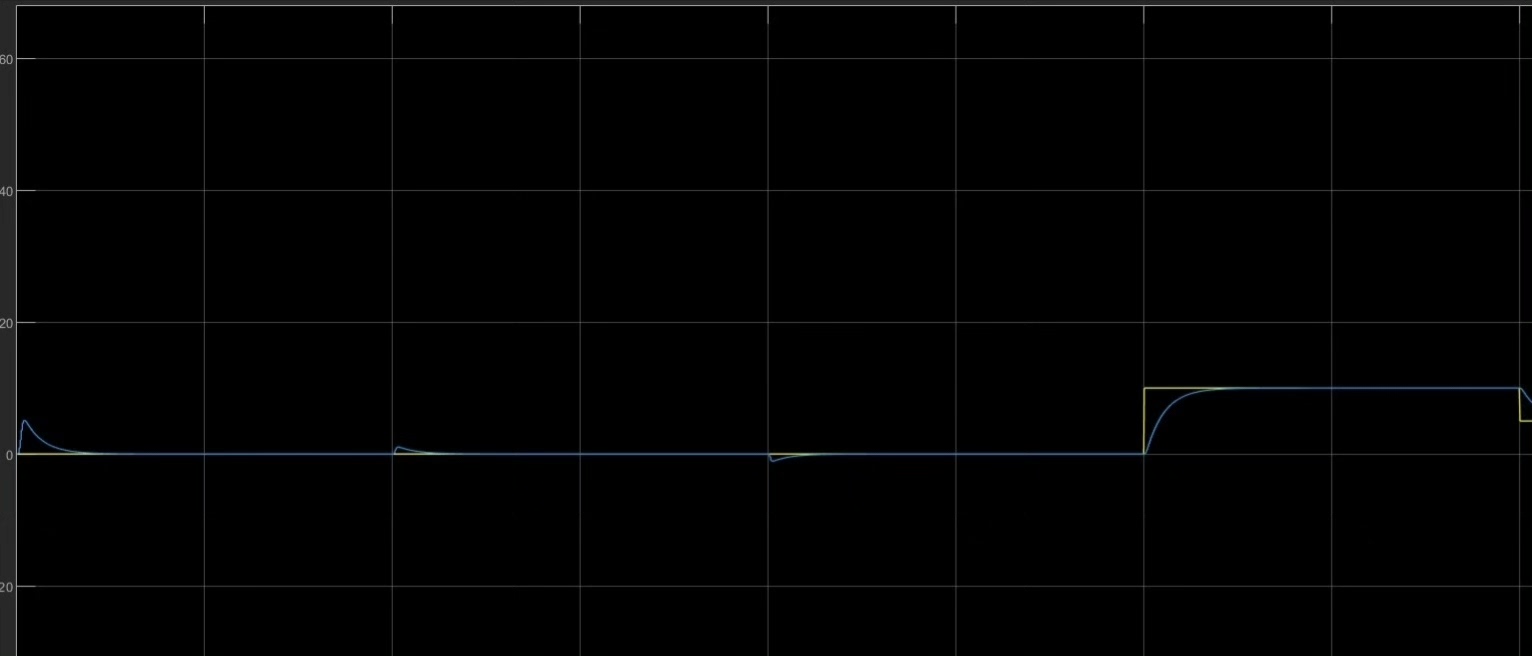
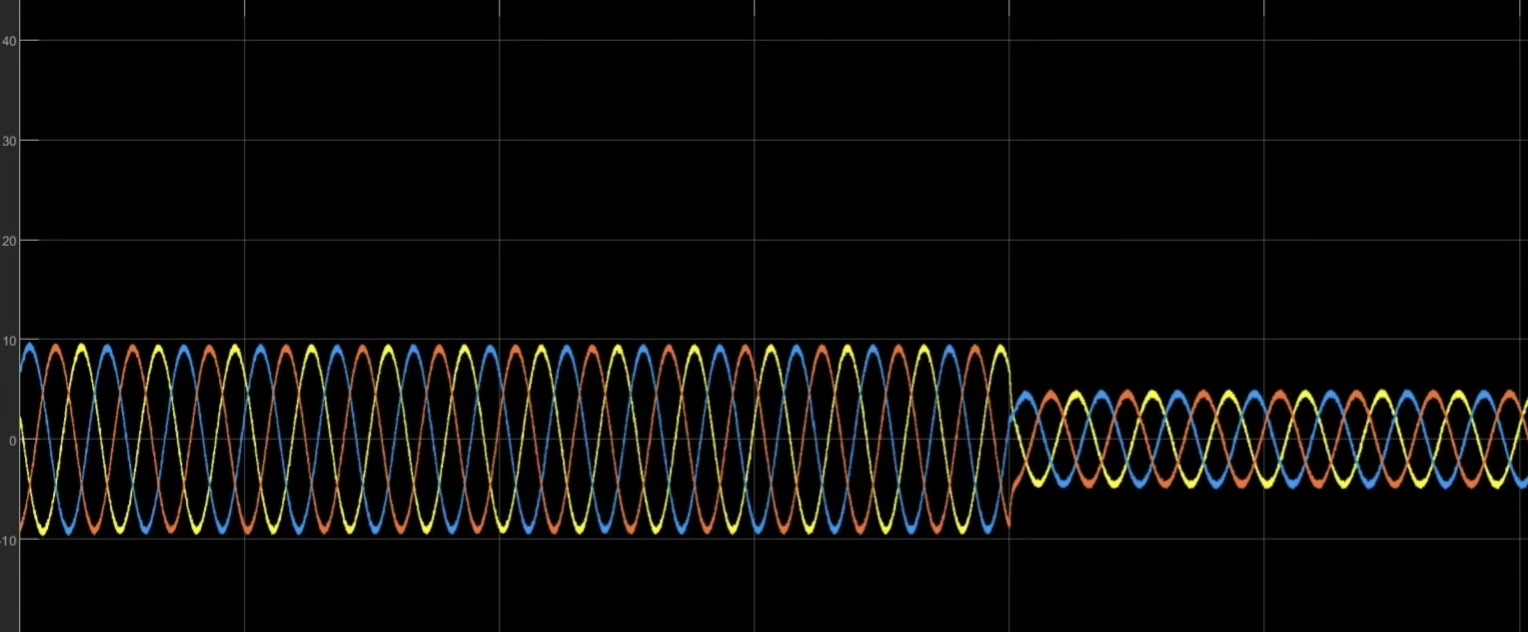
电流内环 - 无差拍控制

电流内环采用无差拍控制，它的优势在于能够快速跟踪电流指令。无差拍控制的核心思想是根据系统模型预测下一时刻的状态，并在当前时刻施加合适的控制量，使得下一时刻的输出恰好等于给定值。

以三相PMSM为例，假设已知电机的电压方程和磁链方程，我们可以推导出无差拍控制的电压指令计算公式。

matlab 复制代码

% 这里以Matlab代码示意无差拍控制电压指令计算
% 已知电机参数和当前电流、磁链等
Rs = 0.1; % 定子电阻
Ld = 0.008; % d轴电感
Lq = 0.008; % q轴电感
psi_f = 0.175; % 永磁体磁链
omega_r = 100; % 转子电角速度

% 当前电流
id = 0;
iq = 1;

% 计算无差拍控制电压指令
vd = -Rs * id + Lq * omega_r * iq;
vq = -Rs * iq - Ld * omega_r * id + omega_r * psi_f;

这里计算出的vd和vq就是施加到电机的d轴和q轴电压指令，通过这样的计算，能快速地让电流跟踪上指令值。

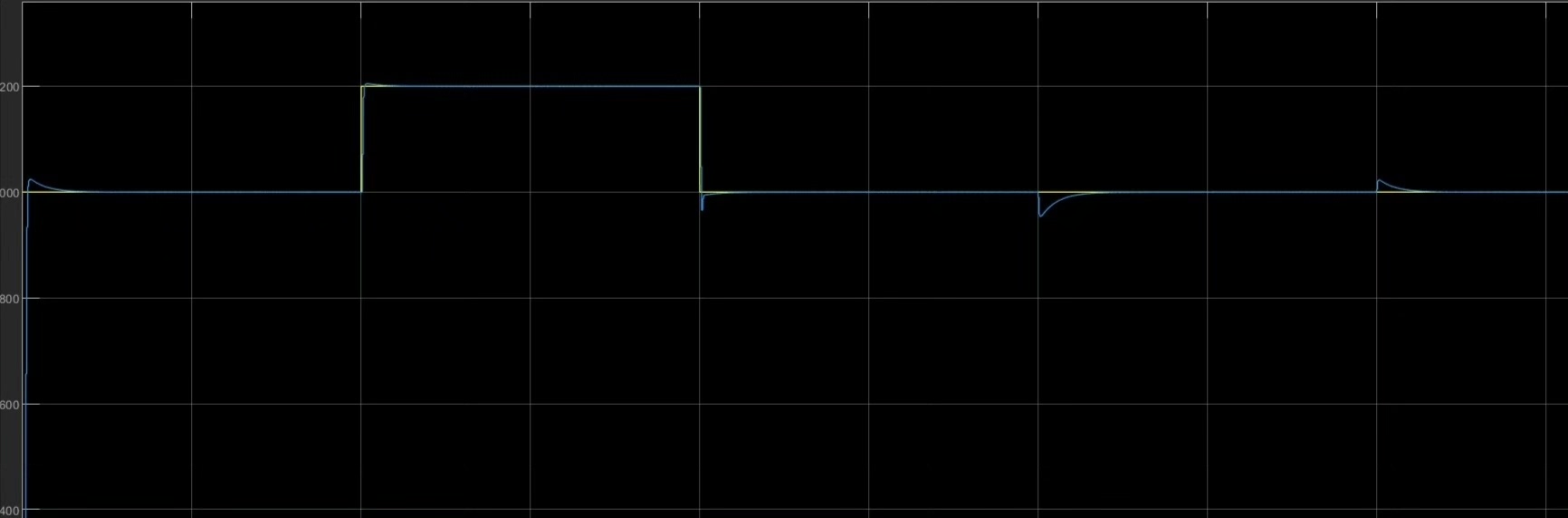
扰动观测器的作用

在实际运行中，PMSM会受到各种扰动，比如负载变化等。扰动观测器就像是一个"侦察兵"，能够实时观测到这些扰动，并将其补偿到控制量中。

以基于扩张状态观测器（ESO）的扰动观测为例，我们可以设计如下形式的ESO：

python 复制代码

# Python代码示意ESO基本结构
beta1 = 300
beta2 = 3000
beta3 = 10000

z1 = 0
z2 = 0
z3 = 0

def eso(y, u):
    global z1, z2, z3
    e = z1 - y
    z1 = z1 - Ts * (z2 - beta1 * e)
    z2 = z2 - Ts * (z3 - beta2 * e + 1.5 * u)
    z3 = z3 - Ts * beta3 * e
    return z3

这里y是系统输出（比如速度或电流），u是控制输入。通过ESO实时估计出扰动z3，然后在控制算法中对其进行补偿，从而提高系统的抗干扰能力。

通过这样速度外环MPC、电流内环无差拍控制，再结合扰动观测器的设计，整个PMSM控制系统不仅控制效果理想，而且模块程序设计清晰易懂，方便我们进一步学习和优化。无论是深入研究电机控制理论，还是实际工程应用，都能从这样的架构中获得不少启发。