3 链表二叉树

环形链表是链表中的一类特殊问题，它和链表反转一样，有着相对恒定的解题思路和适当的变体。如果你对它的特性和解法没有预先的了解和把握，那么前期的推导可能会花去你大量的时间。反过来看，只要我们能够掌握其核心思路，那么不管它怎么变化，大家都能在瞬间找到解题的"抓手"、进而给出正确的解答。

环形链表基本问题------如何判断链表是否成环？

真题描述：给定一个链表，判断链表中是否有环。
示例 1：

输入：[3,2,0,4]（链表结构如下图）输出：true

解释：链表中存在一个环

思路解读

其实链表成环的特征非常明显，大家可以结合一个现实中的例子来理解：

假如现实中有一个长跑爱好者李雷，这货很狂，他立了一个 flag，说要徒步环游世界：

地球的周长围出来的这个圆，它就是一个"环"。李雷现在就想围着这个环跑上一圈，说他狂，他也没那么狂------他觉得自己最多跑一圈，为了防止自己跑过界，他决定在出发的地方立一个 flag：

这样，不管李雷走完这个环用了多少年，世事如何变迁，只要他的 flag 还没有倒，那么李雷就一定能回到自己梦开始的地方：）。

换个角度看：只要李雷在闷头前进的过程中，发现了 flag 的存在，那么就意味着，李雷确实走了一个环。毕竟若这是一条线，他将永远无法回到起点。

回到链表的世界里，也是一个道理。一个环形链表的基本修养，是能够让遍历它的游标回到原点：

从 flag 出发，只要我能够再回到 flag 处，那么就意味着，我正在遍历一个环形链表。

我们按照这个思路来做题：

编码实现

js 复制代码

/**
 * @param {ListNode} head
 * @return {boolean}
 */
// 入参是头结点 
const hasCycle = function(head) {
    // 只要结点存在，那么就继续遍历
    while(head){
        // 如果 flag 已经立过了，那么说明环存在
        if(head.flag){
            return true;
        }else{
            // 如果 flag 没立过，就立一个 flag 再往
            下走
            head.flag = true;
            head = head.next;
        }
    }
    return false;
};

环形链表衍生问题------定位环的起点

真题描述：给定一个链表，返回链表开始入环的第一个结点。如果链表无环，则返回 null。
示例 1：

输入：head = [3,2,0,-4]（如下图）输出：tail connects to node index 1 解释：链表中有一个环，其尾部连接到第二个结点。
示例 2：

输入：head = [1,2]（如下图）

输出：tail connects to node index 0

解释：链表中有一个环，其尾部连接到第一个结点。
示例 3：

输入：head = [1]（如下图）

输出：no cycle

解释：链表中没有环。

思路解读

这道题在上道题的基础上，仅仅增加了一个"返回链表的成环起点"，其难度定义就从 easy 上升到了 medium。不过对于掌握了关键解题思路的各位来说，这道题仍然是 easy------因为如果一个结点是环形链表成环的起点，那么它一定是第一个被发现 flag 标志已存在的结点：

这一点不难理解，我们试想如果从头开始遍历一个链表，假如途中进入了一个环，那么首先被打上 flag 标签的其实就是环的起点。待我们遍历完这个环时，即便环上所有的结点都已经被立了 flag，但起点处的 flag 一定最先被我们定位到。因此，我们只需要在第一次发现 flag 已存在时，将对应的结点返回即可：

编码实现

js 复制代码

/**
 * @param {ListNode} head
 * @return {ListNode}
 */
const detectCycle = function(head) {
    while(head){
        if(head.flag){
            return head;
        }else{
            head.flag = true;
            head = head.next;
        }
    }
    return null;
};

快慢指针的思路

这道题还有一个公认的比较经典的思路，就是用快慢指针来做：

定义慢指针 slow，快指针 fast。两者齐头并进， slow 一次走一步、fast 一次走两步。这样如果它们是在一个有环的链表里移动，一定有相遇的时刻。这个原理证明起来也比较简单：我们假设移动的次数为 t，slow 移动的路程就是t，fast 移动的路程为2t，假如环的长度为 s，那么当下面这个条件：

js 复制代码

2t - t = s

也就是：

js 复制代码

t = s

满足时，slow 和 fast 就一定会相遇。反之，如果两者没有相遇，同时 fast 遍历到了链表的末尾，发现 next 指针指向 null，则链表中不存在环。

有兴趣的同学，可以尝试用双指针法实现一遍上面的判定。不过我更加推荐的仍然是"立flag"法，理解难度和编码难度上来说都更加友好，有利于大家实现题目的"秒杀"。

弦外之音

在这一节，大家会发现一个非常有趣的现象------做环形链表的系列题目，难点其实在于你怎么去想明白这个成环的过程、怎么把握成环后的特性。真正编码实现的时候，寥寥数行就可以搞定。这其实也是我想要向大家传达的一个重要的解题习惯------做算法题时，不要急于下手写代码，而应该先静下心来，稳住神、一步一步捋清楚你自己的思路。

之所以要把这点单独拎出来讲，是因为我知道很多同学平时写业务代码比较多。前端业务代码是什么特征？干就完了，对吧？反正就算代码有问题，也可以通过直观的视觉反馈及时发现、及时修复。在肉眼可见的反馈的指导下，你基本不会出什么方向性的问题。

做算法题就大不一样了，真正提交给 OJ 运行之前，除了你自己的逻辑判断之外、没有任何直观的线索能够帮你明确问题的所在。也就是说，如果你一开始压根没想清楚、脑子里本来就是一团乱麻，那么直接开干后往往是越写越乱、最后代码的修复成本也会变得非常高。

盲写代码、乱写代码，不仅容易扰乱自己的思路，也会给面试官留下"这个人怎么这么冒失"一类的负面印象。所以大家一定要尽量规避这种行为，如果实在对自己的思路感到不确定、不自信，这时候可以问对方要张纸、先线下梳理一下。真正面试的时候，我们对于自己敲在屏幕上的每一行代码，都应该抱有敬畏之心。

（阅读过程中有任何想法或疑问，或者单纯希望和笔者交个朋友啥的，欢迎大家添加我的微信xyalinode与我交流哈~）栈与队列相关的问题就比较微妙了，很多时候相关题目中压根不会出现"栈"、"队列"这样的关键字，但只要你深入到真题里去、对栈和队列的应用场景建立起正确的感知，那么很多线索都会在分析的过程中被你轻松地挖掘出来。

这里也和大家分享一位读者在试读过程中的学习感悟：

感觉算法题除了理解还要靠练习，就像高考数学题，要锻炼出解题常规思维。任重道远啊🙊

其实就是这么回事，这也正是我们开篇就跟大家指明"以题为纲"这条路的初衷。

好啦，开工了老哥们！

典型真题快速上手-"有效括号"问题

题目描述：给定一个只包括 '('，')'，'{'，'}'，'['，']' 的字符串，判断字符串是否有效。
有效字符串需满足：左括号必须用相同类型的右括号闭合。

左括号必须以正确的顺序闭合。

注意空字符串可被认为是有效字符串。
示例 1:

输入: "()"

输出: true
示例 2:

输入: "()[]{}"

输出: true
示例 3:

输入: "(]"

输出: false
示例 4:

输入: "([)]"

输出: false

示例 5:

输入: "{[]}"

输出: true

思路分析

括号问题在面试中出现频率非常高，这类题目我们一般首选用栈来做。

为什么可以用栈做？大家想想，括号成立意味着什么？意味着对称性。

巧了，根据栈的后进先出原则，一组数据的入栈和出栈顺序刚好是对称的。比如说1、2、3、4、5、6按顺序入栈，其对应的出栈序列就是 6、5、4、3、2、1：

js 复制代码

123456
654321

对称关系一目了然。

因此这里大家可以记下一个规律：题目中若涉及括号问题，则很有可能和栈相关。

回到题目中来，我们的思路就是在遍历字符串的过程中，往栈里 push 括号对应的配对字符。比如如果遍历到了 (，就往栈里 push )。

假如字符串中所有的括号都成立，那么前期我们 push 进去的一定全都是左括号、后期 push 进去的一定全都是右括号。而且左括号的入栈顺序，和其对应的右括号的入栈顺序应该是相反的，比如这个例子：

css 复制代码

({[]})

最后一个入栈的左方括号[，与之匹配的右方括号]正是接下来第一个入栈的右括号。

因此，我们可以果断地认为在左括号全部入栈结束时，栈顶的那个左括号，就是第一个需要被配对的左括号。此时我们需要判断的是接下来入栈的第一个右括号是否和此时栈顶的左括号配对。如果配对成功，那么这一对括号就是有效的，否则直接 return false。

当判断出一对有效的括号之后，我们需要及时地丢掉它，去判断其它括号是否有效。这里这个"丢掉"的动作，就对应着两个括号一起出栈的过程。

每配对成功一对括号，我们都将这对括号出栈。这样一来，我们就可以确保栈顶的括号总是下一个需要被匹配的左括号。

如果说我们出栈到最后，栈不为空，那么意味着一部分没有被匹配上的括号被剩下来了，说明字符串中并非所有的括号都有效，判断 false；反之，则说明所有的括号都配对成功了，判断为 true。

编码实现

js 复制代码

// 用一个 map 来维护左括号和右括号的对应关系
const leftToRight = {
  "(": ")",
  "[": "]",
  "{": "}"
};

/**
 * @param {string} s
 * @return {boolean}
 */
const isValid = function(s) {
  // 结合题意，空字符串无条件判断为 true
  if (!s) {
    return true;
  }
  // 初始化 stack 数组
  const stack = [];
  // 缓存字符串长度
  const len = s.length;
  // 遍历字符串
  for (let i = 0; i < len; i++) {
    // 缓存单个字符
    const ch = s[i];
    // 判断是否是左括号，这里我为了实现加速，没有用数组的 includes 方法，直接手写判断逻辑
    if (ch === "(" || ch === "{" || ch === "[") stack.push(leftToRight[ch]);
    // 若不是左括号，则必须是和栈顶的左括号相配对的右括号
    else {
      // 若栈为空，或栈顶的左括号没有和当前字符匹配上，那么判为无效
      if (!stack.length || stack.pop() !== ch) {
        return false;
      }
    }
  }
  // 若所有的括号都能配对成功，那么最后栈应该是空的
  return !stack.length;
};

栈问题进阶-每日温度问题

题目描述: 根据每日气温列表，请重新生成一个列表，对应位置的输出是需要再等待多久温度才会升高超过该日的天数。如果之后都不会升高，请在该位置用 0 来代替。
例如，给定一个列表 temperatures = [73, 74, 75, 71, 69, 72, 76, 73]，你的输出应该是 [1, 1, 4, 2, 1, 1, 0, 0]。
提示：气温列表长度的范围是 [1, 30000]。每个气温的值的均为华氏度，都是在 [30, 100] 范围内的整数。

思路分析

看到这道题，大家不难想到暴力遍历法：直接两层遍历，第一层定位一个温度，第二层定位离这个温度最近的一次升温是哪天，然后求出两个温度对应索引的差值即可。

一个数组两层遍历，属于比较少见且高危的操作。事出反常必有妖，此时我们就需要反思：这道题是不是压根不该用暴力遍历来做？

答案是肯定的。因为在这个暴力遍历的过程中，我们其实做了很多"多余"的事情。

拿第三个索引位上这个 75 来说，我们在定位比 75 高的第一个温度的过程中，就路过了 71、69、72 这三个温度，其中，72 正是 71 对应的目标温度，可我们却像没看见它一样、啥也没干。只有等最外层遍历走到 71 时，我们才又重复了一遍刚刚走过的路、确认了 71 和 72 之间的关系------像这种不必要的重复，我们要想办法把它干掉。

栈结构可以帮我们避免重复操作 。

避免重复操作的秘诀就是及时地将不必要的数据出栈，避免它对我们后续的遍历产生干扰。

拿这道题来说，我们的思路就是：尝试去维持一个递减栈 。

当遍历过的温度，维持的是一个单调递减 的态势时，我们就对这些温度的索引下标执行入栈操作；只要出现了一个数字，它打破了这种单调递减的趋势，也就是说它比前一个温度值高，这时我们就对前后两个温度的索引下标求差，得出前一个温度距离第一次升温的目标差值。这么说可能有点抽象，我们用一张动图来理解一下这个过程（这个过程实际有将近一分钟那么长，贴上来之后我发现完全加载不出来，这里呈现的是截止到第一个元素出栈的片段，完整的视频我这边上传到了小破站）：

在这个过程中，我们仅对每一个温度执行最多一次入栈操作、一次出栈操作，整个数组只会被遍历一次，因此时间复杂度就是O(n)。相对于两次遍历带来的 O(n^2)的开销来看，栈结构真是帮了咱们大忙了。

编码实现

js 复制代码

/**
 * @param {number[]} T
 * @return {number[]}
 */
// 入参是温度数组
const dailyTemperatures = function(T) {
    const len = T.length // 缓存数组的长度 
    const stack = [] // 初始化一个栈   
    const res = (new Array(len)).fill(0) //  初始化结果数组，注意数组定长，占位为0
    for(let i=0;i<len;i++) {
      // 若栈不为0，且存在打破递减趋势的温度值
      while(stack.length && T[i] > T[stack[stack.length-1]]) {
        // 将栈顶温度值对应的索引出栈
        const top = stack.pop()  
        // 计算 当前栈顶温度值与第一个高于它的温度值 的索引差值
        res[top] = i - top 
      }
      // 注意栈里存的不是温度值，而是索引值，这是为了后面方便计算
      stack.push(i)
    }
    // 返回结果数组
    return res 
};

栈的设计------"最小栈"问题

题目描述：设计一个支持 push ，pop ，top 操作，并能在常数时间内检索到最小元素的栈。
push(x) ------ 将元素 x 推入栈中。

pop() ------ 删除栈顶的元素。

top() ------ 获取栈顶元素。

getMin() ------ 检索栈中的最小元素。
示例:

MinStack minStack = new MinStack();

minStack.push(-2);

minStack.push(0);

minStack.push(-3);

minStack.getMin(); --> 返回 -3.

minStack.pop();

minStack.top(); --> 返回 0.

minStack.getMin(); --> 返回 -2.

思路分析

这道题并不难，但是综合性很强，整个题做下来能够相对全面地考察到候选人对栈结构、栈操作的理解和掌握，是不少一面/少数二面面试官的心头好。

其中前三个操作：push、pop 和 top，我们在数据结构快速上手环节已经给大家讲过了，这里不多赘述。需要展开讲的是 getMin 这个接口，这个接口有时候会直接单独拎出来作为一道题来考察，需要大家对它的实现思路有一个真正扎实的掌握。

getMin 要做的事情，是从一个栈里找出其中最小的数字。我们仍然是抛砖引玉，先说一个大部分人都能想到的思路：

初始化一个最小值变量，它的初始值可以设一个非常大的数（比如 Infinity），然后开始遍历整个栈。在遍历的过程中，如果遇到了更小的值，就把最小值变量更新为这个更小的值。这样遍历结束后，我们就能拿到栈中的最小值了。

这个过程中，我们对栈进行了一次遍历，时间复杂度无疑是 O(n)。

按照这个思路，整个栈的设计我们可以这样写：

编码实现1

js 复制代码

/**
 * 初始化你的栈结构
 */
const MinStack = function() {
  this.stack = []
};

/** 
 * @param {number} x
 * @return {void}
 */
// 栈的入栈操作，其实就是数组的 push 方法
MinStack.prototype.push = function(x) {
  this.stack.push(x)
};

/**
 * @return {void}
 */
// 栈的入栈操作，其实就是数组的 pop 方法
MinStack.prototype.pop = function() {
  this.stack.pop()
};

/**
 * @return {number}
 */
// 取栈顶元素，咱们教过的哈，这里我本能地给它一个边界条件判断（其实不给也能通过，但是多做不错哈）
MinStack.prototype.top = function() {
  if(!this.stack || !this.stack.length) {
      return 
  }
  return this.stack[this.stack.length - 1]
};

/**
 * @return {number}
 */
// 按照一次遍历的思路取最小值
MinStack.prototype.getMin = function() {
    let minValue = Infinity  
    const  { stack } = this
    for(let i=0; i<stack.length;i++) {
        if(stack[i] < minValue) {
            minValue = stack[i]
        }
    }
    return minValue
};

这样写，用例也能跑通，但是不够酷。如果你在面试时这样做了，面试官有99%的可能性会追问你这句：

"这道题有没有时间效率更高的做法？"

人家都这样问了，咱当然要说"有"。然后，面试官就会搬个小板凳，坐你旁边看你如何妙手回春，变 O(n) 为 O(1)。

时间效率的提升，从来都不是白嫖，它意味着我们要付出更多的空间占用作为代价。在这道题里，如果继续沿着栈的思路往下走，我们可以考虑再搞个栈（stack2）出来作为辅助，让这个栈去容纳当前的最小值。

如何确保 stack2 能够确切地给我们提供最小值？这里我们需要实现的是一个从栈底到栈顶呈递减趋势的栈（敲黑板！递减栈出现第二次了哈）：

取最小值：由于整个栈从栈底到栈顶递减，因此栈顶元素就是最小元素。
若有新元素入栈：判断是不是比栈顶元素还要小，否则不准进入 stack2。
若有元素出栈：判断是不是和栈顶元素相等，如果是的话，stack2 也要出栈。

按照这个思路，我们可以有以下编码：

编码实现2

js 复制代码

const MinStack = function() {
    this.stack = [];
    // 定义辅助栈
    this.stack2 = [];
};

/** 
 * @param {number} x
 * @return {void}
 */
MinStack.prototype.push = function(x) {
    this.stack.push(x);
    // 若入栈的值小于当前最小值，则推入辅助栈栈顶
    if(this.stack2.length == 0 || this.stack2[this.stack2.length-1] >= x){
        this.stack2.push(x);
    }
};

/**
 * @return {void}
 */
MinStack.prototype.pop = function() {
    // 若出栈的值和当前最小值相等，那么辅助栈也要对栈顶元素进行出栈，确保最小值的有效性
    if(this.stack.pop() == this.stack2[this.stack2.length-1]){
        this.stack2.pop();
    }
};

/**
 * @return {number}
 */
MinStack.prototype.top = function() {
    return this.stack[this.stack.length-1];
};

/**
 * @return {number}
 */
MinStack.prototype.getMin = function() {
    // 辅助栈的栈顶，存的就是目标中的最小值
    return this.stack2[this.stack2.length-1];
};

（阅读过程中有任何想法或疑问，或者单纯希望和笔者交个朋友啥的，欢迎大家添加我的微信xyalinode与我交流哈~）结束了针对栈结构的定点轰炸，我们现在开始要缓缓过渡到队列的世界了。

关于队列，在算法面试中大家需要掌握以下重点：

栈向队列的转化
双端队列
优先队列

以上考点中，1 属于基础难度， 2 对一部分同学来说已经有点吃力，3 的区分度最高------优先队列属于高级数据结构，其本质是二叉堆结构，考虑到相关题目具有较强的综合性，我们把它放在小册二叉树和堆相关的专题来展开。在本节，我们集中火力向前两个命题点开炮。

为什么一道题可以成为高频面试题

如何用栈实现队列？这个问题在近几年的算法面试中热度非常高。

所谓"热度"从何而来？这里就引出了一个非常有趣的话题：（在前端算法面试中）什么样的题目是好题？

首先，不能剑走偏锋：好的面试题，它考察的大多是算法/数据结构中最经典、最关键的一部分内容，这样才能体现公平；其次，它的知识点要尽可能密集、题目本身要尽可能具备综合性，这样才能一箭双雕甚至一箭N雕，进而体现区分度、最大化面试过程的效率。

能够同时在这两个方面占尽优势的考题其实并不是很多，"用栈实现队列"这样的问题算是其中的佼佼者：一方面，它考察的确实是数据结构中的经典内容；另一方面，它又覆盖了两个大的知识点、足以检验出候选人编码基本功的扎实程度。唯一的 BUG 可能就是深度和复杂度不够，换句话说就是不够难。

这个特点，在普通算法面试中可能是 BUG，但在前端算法面试中，实在未必。大家要知道，你是前端，你的面试官也是前端，前端行业普遍的算法水平是啥样他心里还没个数吗...... 实际上大多数前端算法面试题的风格都是非常务实的，需要你炫技的实属特殊情况。

如何用栈实现一个队列？

题目描述：使用栈实现队列的下列操作：

push(x) -- 将一个元素放入队列的尾部。

pop() -- 从队列首部移除元素。

peek() -- 返回队列首部的元素。

empty() -- 返回队列是否为空。
示例: MyQueue queue = new MyQueue();

queue.push(1);

queue.push(2);

queue.peek(); // 返回 1

queue.pop(); // 返回 1

queue.empty(); // 返回 false
说明:

你只能使用标准的栈操作 -- 也就是只有 push to top, peek/pop from top, size, 和 is empty 操作是合法的。

你所使用的语言也许不支持栈。你可以使用 list 或者 deque（双端队列）来模拟一个栈，只要是标准的栈操作即可。

假设所有操作都是有效的（例如，一个空的队列不会调用 pop 或者 peek 操作）。

思路分析

做这道题大家首先要在心里清楚一个事情：栈和队列的区别在哪里？

仔细想想，栈，后进先出；队列，先进先出。也就是说两者的进出顺序其实是反过来的。用栈实现队列，说白了就是用栈实现先进先出的效果，再说直接点，就是想办法让栈底的元素首先被取出 ，也就是让出栈序列被逆序。

乍一看有点头大：栈结构决定了栈底元素只能被死死地压在最底下，如何使它首先被取出呢？

一个栈做不到的事情，我们用两个栈来做：

首先，准备两个栈：

现在问题是，怎么把第一个栈底下的那个 1 给撬出来。仔细想想，阻碍我们接触到 1 的是啥？是不是它头上的 3 和 2？那么如何让 3 和 2 给 1 让路呢？实际上咱们完全可以把这三个元素按顺序从 stack1 中出栈、然后入栈到 stack 2 里去：

此时 1 变得触手可及。不仅如此，下一次我们试图出队 2 的时候，可以继续直接对 stack2 执行出栈操作------因为转移 2 和 3 的时候已经做过一次逆序了，此时 stack2 的出栈序列刚好就对应队列的出队序列。
有同学会问，那如果 stack1 里入栈新元素怎么办？比如这样：

你会发现这个4按照顺序应该在 1、2、3 后出栈。当 4 需要被出栈时，stack2 一定已经空掉了。当 stack2 为空、而 stack1 不为空时，我们需要继续把 stack1 中的元素转移到 stack2 中去，然后再从 stack2 里取元素。也就是说，所有的出队操作都只能依赖 stack2 来完成------只要我们坚持这个原则，就可以确保 stack1 里的元素都能够按照正确的顺序（逆序）出栈。

我们按照这个思路来写代码：

编码实现

js 复制代码

/**
 * 初始化构造函数
 */
const MyQueue = function () {
  // 初始化两个栈
  this.stack1 = [];
  this.stack2 = [];
};

/**
* Push element x to the back of queue.
* @param {number} x
* @return {void}
*/
MyQueue.prototype.push = function (x) {
  // 直接调度数组的 push 方法
  this.stack1.push(x);
};

/**
* Removes the element from in front of queue and returns that element.
* @return {number}
*/
MyQueue.prototype.pop = function () {
  // 假如 stack2 为空，需要将 stack1 的元素转移进来
  if (this.stack2.length <= 0) {
    // 当 stack1 不为空时，出栈
    while (this.stack1.length !== 0) {
      // 将 stack1 出栈的元素推入 stack2
      this.stack2.push(this.stack1.pop());
    }
  }
  // 为了达到逆序的目的，我们只从 stack2 里出栈元素
  return this.stack2.pop();
};

/**
* Get the front element.
* @return {number}
* 这个方法和 pop 唯一的区别就是没有将定位到的值出栈
*/
MyQueue.prototype.peek = function () {
  if (this.stack2.length <= 0) {
    // 当 stack1 不为空时，出栈
    while (this.stack1.length != 0) {
      // 将 stack1 出栈的元素推入 stack2
      this.stack2.push(this.stack1.pop());
    }
  }
  // 缓存 stack2 的长度
  const stack2Len = this.stack2.length;
  return stack2Len && this.stack2[stack2Len - 1];
};

/**
* Returns whether the queue is empty.
* @return {boolean}
*/
MyQueue.prototype.empty = function () {
  // 若 stack1 和 stack2 均为空，那么队列空
  return !this.stack1.length && !this.stack2.length;
};

认识双端队列

双端队列衍生出的滑动窗口问题，是一个经久不衰的命题热点。关于双端队列，各种各样的解释五花八门，这里大家不要纠结，就记住一句话：

双端队列就是允许在队列的两端进行插入和删除的队列。

体现在编码上，最常见的载体是既允许使用 pop、push 同时又允许使用 shift、unshift 的数组：

js 复制代码

const queue = [1,2,3,4] // 定义一个双端队列   
queue.push(1) // 双端队列尾部入队 
queue.pop() // 双端队列尾部出队   
queue.shift() // 双端队列头部出队 
queue.unshift(1) // 双端队列头部入队

现在相信你对双端队列已经形成了一个感性的认知，咱们紧接着就开始做题，在题里去认知这种结构的特征和效用。

滑动窗口问题

题目描述：给定一个数组 nums 和滑动窗口的大小 k，请找出所有滑动窗口里的最大值。
示例: 输入: nums = [1,3,-1,-3,5,3,6,7], 和 k = 3 输出: [3,3,5,5,6,7]
解释: 滑动窗口的位置

$1 3 -1\] -3 5 3 6 7 1 \[3 -1 -3\] 5 3 6 7 1 3 \[-1 -3 5\] 3 6 7 1 3 -1 \[-3 5 3\] 6 7 1 3 -1 -3 \[5 3 6\] 7 1 3 -1 -3 5 \[3 6 7$
最大值分别对应：

3 3 5 5 6 7
提示：你可以假设 k 总是有效的，在输入数组不为空的情况下，1 ≤ k ≤ 输入数组的大小。

思路分析：双指针+遍历法

这道题如果只是为了做对，那么思路其实不难想，我们直接模拟题中描述的这个过程就行。

按照题意，它要求我们在遍历数组的过程当中，约束一个窗口------窗口的本质其实就是一个范围，像这样：

csharp 复制代码

[1  3  -1] -3  5  3  6  7

范围就被圈定在了前三个元素。

我们前面学过，约束范围，可以用双指针。因此我这里定义一个 left 左指针、定义一个 right 右指针，分别指向窗口的两端即可：

接下来我们可以把这个窗口里的数字取出来，直接遍历一遍、求出最大值，然后把最大值存进结果数组。这样第一个窗口的最大值就有了。

接着按照题意，窗口每次前进一步（左右指针每次一起往前走一步），此时的范围变成了这样：

我们要做的仍然是取出当前范围的所有元素、遍历一遍求出最大值，然后将最大值存进结果数组。

反复执行上面这个过程，直到数组完全被滑动窗口遍历完毕，我们也就得到了问题的答案。

基于这个淳朴的思路，我们来写一波代码：

编码实现：双指针+遍历法

js 复制代码

/**
 * @param {number[]} nums
 * @param {number} k
 * @return {number[]}
 */
const maxSlidingWindow = function (nums, k) {
  // 缓存数组的长度
  const len = nums.length;
  // 定义结果数组
  const res = [];
  // 初始化左指针
  let left = 0;
  // 初始化右指针
  let right = k - 1;
  // 当数组没有被遍历完时，执行循环体内的逻辑
  while (right < len) {
    // 计算当前窗口内的最大值
    const max = calMax(nums, left, right);
    // 将最大值推入结果数组
    res.push(max);
    // 左指针前进一步
    left++;
    // 右指针前进一步
    right++;
  }
  // 返回结果数组
  return res;
};

// 这个函数用来计算最大值
function calMax(arr, left, right) {
  // 处理数组为空的边界情况
  if (!arr || !arr.length) {
    return;
  }
  // 初始化 maxNum 的值为窗口内第一个元素
  let maxNum = arr[left];
  // 遍历窗口内所有元素，更新 maxNum 的值
  for (let i = left; i <= right; i++) {
    if (arr[i] > maxNum) {
      maxNum = arr[i];
    }
  }
  // 返回最大值
  return maxNum;
}

解法复盘

上面这个解法，你在面试的时候写上去，完全没有问题，也不用担心超时。

有的同学可能会觉得 calMax 这个函数多余了，认为可以直接用 Math.max 这个 JS 原生方法。其实就算是Math.max，也不可避免地需要对你传入的多个数字做最小值查找，calMax 和Math.max做的工作可以说是一样的辛苦。我这里手动实现一个 calMax，大家会对查找过程造成的时间开销有更直观的感知。

现在我们来思考一下，上面这一波操作下来，时间复杂度是多少？

这波操作里其实涉及了两层循环，外层循环是 while，它和滑动窗口前进的次数有关。滑动窗口前进了多少次，while 就执行了多少次。

假设数组的规模是 n，那么从起始位置开始，滑动窗口每次走一步，一共可以走 n - k 次。注意别忘了初始位置也算作一步的，因此一共走了 n - k + 1次。然后每个窗口内部我们又会固定执行 k 次遍历。注意 k 可不是个常数，它和 n 一样是个变量。因此这个时间复杂度简化后用大 O 表示法可以记为 O(kn)。

O(kn) 虽然不差，但对这道题来说，还不是最好。因此在面试过程中，如果你采用了上面这套解法做出了这个题，面试官有 99% 的可能性会追问你：这个题可以优化吗？如何优化？（或者直接问你，你能在线性时间复杂度内解决此题吗？）

答案当然是能，然后面试官就会搬个小板凳坐你旁边，看看你怎么妙手回春，变 O(kn) 为 O(n)。

接下来你需要表演的，正是面试官期待已久的双端队列解法啊！

思路分析：双端队列法

要想变 O(kn) 为 O(n)，我们就要想怎么做才能丢掉这个 k。
k 之所以会产生，是因为我们现在只能通过遍历来更新最大值。那么更新最大值，有没有更高效的方法呢？

大家仔细想想，当滑动窗口往后前进一步的时候，比如我从初始位置前进到第二个位置：

（图中红色的范围是初始位置时，滑动窗口覆盖到的元素）

此时滑动窗口内的元素少了一个 1，增加了一个 -3------减少的数不是当前最大值，增加的数也没有超越当前最大值，因此最大值仍然是 3。此时我们不禁要想：如果我们能在窗口发生移动时，只根据发生变化的元素对最大值进行更新，那复杂度是不是就低很多了？

双端队列可以完美地帮助我们达到这个目的。

使用双端队列法，核心的思路是维护一个有效的递减队列。

在遍历数组的前期，我们尝试将遍历到的每一个元素都推入队列内部（下图是第一个元素入队的示意图）：

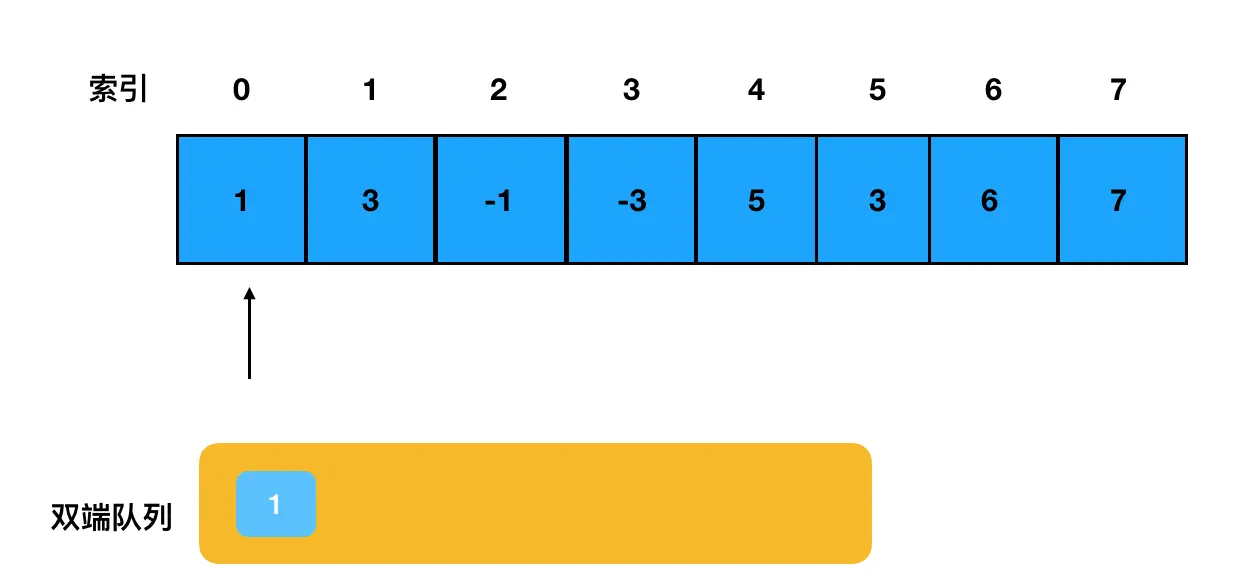每尝试推入一个元素前，都把这个元素与队列尾部的元素作对比。根据对比结果的不同，采取不同的措施：

如果试图推入的元素（当前元素）大于队尾元素，则意味着队列的递减趋势被打破了。此时我们需要将队列尾部的元素依次出队（注意由于是双端队列，所以队尾出队是没有问题的）、直到队尾元素大于等于当前元素为止，此时再将当前元素入队。
如果试图推入的元素小于队列尾部的元素，那么就不需要额外的操作，直接把当前元素入队即可。

我用动画来表达一下这个过程：

（注：动画大小已经极致压缩，如果仍然存在加载失败问题，可能与网络环境有关。如果你遇到了这个问题，建议 PC 端点击这里直接访问动图试试看）

维持递减队列的目的，就在于确保队头元素始终是当前窗口的最大值 。

当遍历到的元素个数达到了 k 个时，意味着滑动窗口的第一个最大值已经产生了，我们把它 push 进结果数组里：

然后继续前进，我们发现数组索引 0 处的元素（1）已经被踢出滑动窗口了（图中红色方块对应的是当前滑动窗口覆盖到的元素们）：

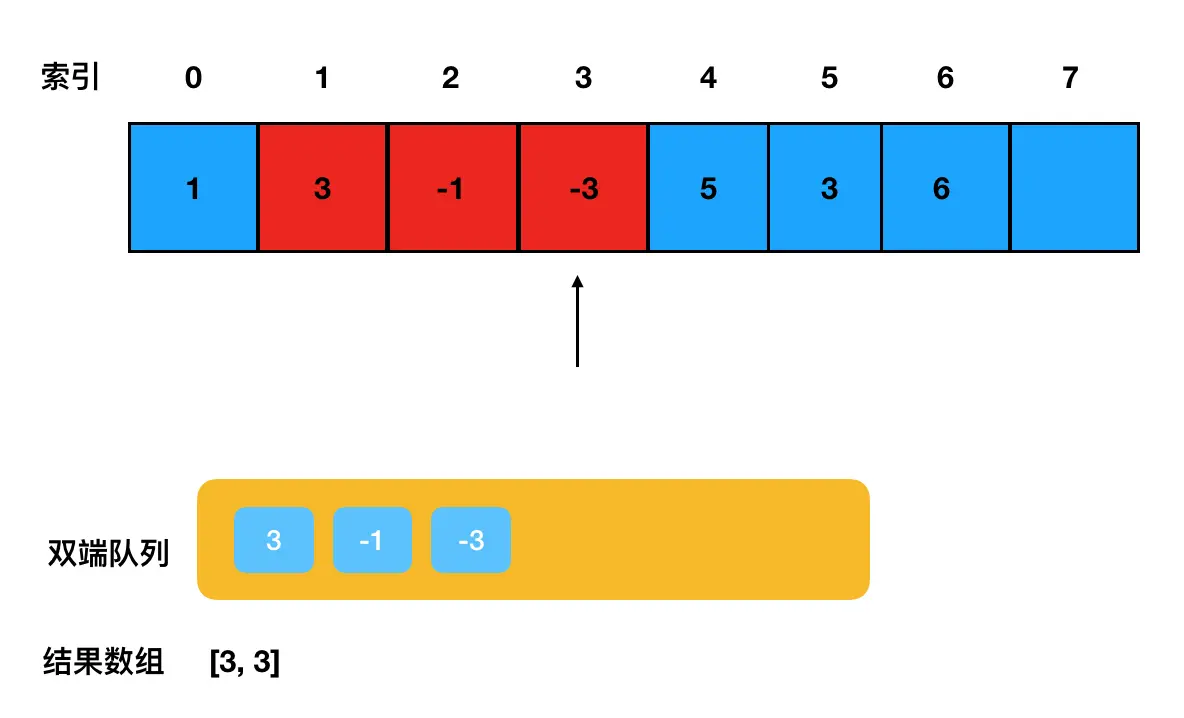为了确保队列的有效性 ，需要及时地去队列检查下 1 这个元素在不在队列里（在的话要及时地踢出去，因为队列本身只维护当前滑动窗口内的元素）。

这里大家思考一下，我在查找 1 的时候，需不需要遍历整个队列？答案是不需要，因为 1 是最靠前的一个元素，如果它在，那么它一定是队头元素。这里我们只需要检查队头元素是不是 1 就行了。此时我们检查队头，发现是 3：

没错，1早就因为不符合递减趋势被从队头干掉了。此时我们可以断定，当前双端队列里的元素都是滑动窗口已经覆盖的有效元素------没毛病，继续往下走就行了。

接下来，每往前遍历一个元素，都需要重复以上的几个步骤。这里我总结一下每一步都做了什么：

检查队尾元素，看是不是都满足大于等于当前元素的条件。如果是的话，直接将当前元素入队。否则，将队尾元素逐个出队、直到队尾元素大于等于当前元素为止。
将当前元素入队
检查队头元素，看队头元素是否已经被排除在滑动窗口的范围之外了。如果是，则将队头元素出队。
判断滑动窗口的状态：看当前遍历过的元素个数是否小于 k。如果元素个数小于k，这意味着第一个滑动窗口内的元素都还没遍历完、第一个最大值还没出现，此时我们还不能动结果数组，只能继续更新队列；如果元素个数大于等于k，这意味着滑动窗口的最大值已经出现了，此时每遍历到一个新元素（也就是滑动窗口每往前走一步）都要及时地往结果数组里添加当前滑动窗口对应的最大值（最大值就是此时此刻双端队列的队头元素）。

这四个步骤分别有以下的目的：

维持队列的递减性：确保队头元素是当前滑动窗口的最大值。这样我们每次取最大值时，直接取队头元素即可。
这一步没啥好说的，就是在维持队列递减性的基础上、更新队列的内容。
维持队列的有效性：确保队列里所有的元素都在滑动窗口圈定的范围以内。
排除掉滑动窗口还没有初始化完成、第一个最大值还没有出现的特殊情况。

结合以上的分析，我们来写代码：

编码实现

js 复制代码

/**
 * @param {number[]} nums
 * @param {number} k
 * @return {number[]}
 */
const maxSlidingWindow = function (nums, k) {
  // 缓存数组的长度
  const len = nums.length;
  // 初始化结果数组
  const res = [];
  // 初始化双端队列
  const deque = [];
  // 开始遍历数组
  for (let i = 0; i < len; i++) {
    // 当队尾元素小于当前元素时
    while (deque.length && nums[deque[deque.length - 1]] < nums[i]) {
      // 将队尾元素（索引）不断出队，直至队尾元素大于等于当前元素
      deque.pop();
    }
    // 入队当前元素索引（注意是索引）
    deque.push(i);
    // 当队头元素的索引已经被排除在滑动窗口之外时
    while (deque.length && deque[0] <= i - k) {
      // 将队头元素索引出队
      deque.shift();
    }
    // 判断滑动窗口的状态，只有在被遍历的元素个数大于 k 的时候，才更新结果数组
    if (i >= k - 1) {
      res.push(nums[deque[0]]);
    }
  }
  // 返回结果数组
  return res;
};

（阅读过程中有任何想法或疑问，或者单纯希望和笔者交个朋友啥的，欢迎大家添加我的微信xyalinode与我交流哈~）

本节我们学习两种关键的基本算法思想：DFS（深度优先搜索）和BFS（广度优先搜索）。这两种算法和栈、队列有着千丝万缕的关系，如果前两节你认真学习掌握了，那么这一节对你来说相信不是问题。

深度优先搜索思想：不撞南墙不回头的"迷宫游戏"

20世纪90年代，小霸王学习机风靡全国。没有哪个小学生，不想拥有一台自己的小霸王学习机------我，也不例外；没有哪个小学生在拥有了小霸王学习机之后，会真的用它来搞学习------我，也不例外。在那个没有王者也没有吃鸡的年代里，小霸王里让我欲罢不能的除了魂斗罗、超级玛丽，还有它------迷宫游戏：

很多同学跟我说他入门算法的时候就挂在 DFS 这里，觉得太高深了，学不动。傻孩子，今天你就会知道，深度优先搜索也不过是在用编码的方式玩一场迷宫游戏。

现在把图上的小黄点想象成你自己，由于你手里没有地图、没有无人机，因此你对迷宫整体的地形一无所知。放眼望去，你眼前只有冰冷的墙壁和并不知道能不能走通的道路。如何走出一条通路？你只能尝试把每一条能走的路都走一遍------也就是所谓的"穷举法"：

以当前位置为起点，闷头往前走
在前进的过程中，难免会遇到岔路口。这个路口可能分叉出去两条、三条、四条甚至更多的道路，你只能选择其中的一条路、然后继续前进（注意，你可能会不止一次遇到岔路口；每遇到一个新的岔路口，你都需要做一次选择）。
你选择的这条路未必是一条通路。如果你走到最后发现此路不通，那么你就要退回到离你最近的那个分叉路口，然后尝试看其它的岔路能不能走通。如果当前的岔路口分叉出去的所有道路都走不通，那么就需要退回到当前岔路口的上一个岔路口，进一步去寻找新的路径。

按照这个思路走下去，只要迷宫是有出口的，你就一定能找到这个出口。在这个过程里，我们贯彻了"不撞南墙不回头"的原则：只要没有碰壁，就决不选择其它的道路，而是坚持向当前道路的深处挖掘------像这样将"深度"作为前进的第一要素的搜索方法，就是所谓的"深度优先搜索"。

深度优先搜索的核心思想，是试图穷举所有的完整路径。

深度优先搜索的本质------栈结构

那么如何使用编码来实现深度优先搜索呢？我们继续讨论迷宫问题，这里我给大家一个抽象过后的简单迷宫结构：

图中蓝色的是入口，灰色的是岔路口，黑色的是死胡同，绿色的是出口。

基于眼前的这个迷宫结构，我们来一步一步模拟一下深度优先搜索的具体过程：

从 A 出发，沿着唯一的一条道路往下走，遇到了第1个岔路口B。眼前有三个选择：C、D、E。这里我按照从上到下的顺序来走（你也可以按照其它顺序），先走C。
发现 C是死胡同，后退到最近的岔路口 B，尝试往D方向走。
发现D 是死胡同，，后退到最近的岔路口 B，尝试往E方向走。
E 是一个岔路口，眼前有两个选择：F 和 G。按照从上到下的顺序来走，先走F。
发现F 是死胡同，后退到最近的岔路口 E，尝试往G方向走。
G 是一个岔路口，眼前有两个选择：H 和 I。按照从上到下的顺序来走，先走H。
发现 H 是死胡同，后退到最近的岔路口 G，尝试往I方向走。
I 就是出口，成功走出迷宫。

大家观察一下这个过程，会不会觉得这些前进、后退的操作，其实和栈结构的入栈、出栈过程非常相似呢？

现在我们把迷宫中的每一个坐标看做是栈里的一个元素，用栈来模拟这个过程：

从 A 出发（A入栈），经过了B（B入栈），接下来面临 C、D、E三条路。这里按照从上到下的顺序来走（你也可以选择其它顺序），先走C（C入栈）。
发现 C是死胡同，后退到最近的岔路口 B（C出栈），尝试往D方向走（D入栈）。
发现D 是死胡同，，后退到最近的岔路口 B（D出栈），尝试往E方向走（E入栈）。
E 是一个岔路口，眼前有两个选择：F 和 G。按照从上到下的顺序来走，先走F（F入栈）。
发现F 是死胡同，后退到最近的岔路口 E（F出栈），尝试往G方向走（G入栈）。
G 是一个岔路口，眼前有两个选择：H 和 I。按照从上到下的顺序来走，先走H（H入栈）。
发现 H 是死胡同，后退到最近的岔路口 G（H出栈），尝试往I方向走（I入栈）。
I 就是出口，成功走出迷宫。

此时栈里面的内容就是A、B、E、G、I，因此 A->B->E->G->I 就是走出迷宫的路径。通过深度优先搜索，我们不仅可以定位到迷宫的出口，还可以记录下相关的路径信息。

现在大家知道了深度优先搜索的过程可以转化为一系列的入栈、出栈操作。那么深度优先搜索在编码上一般会如何实现呢？这里，就需要大家回忆一下第 5 节的内容了------DFS 中，我们往往使用递归来模拟入栈、出栈的逻辑。

DFS 与二叉树的遍历

现在我们站在深度优先搜索的角度，重新理解一下二叉树的先序遍历过程：

从 A 结点出发，访问左侧的子结点；如果左子树同样存在左侧子结点，就头也不回地继续访问下去 。一直到左侧子结点为空时，才退回到距离最近的父结点、再尝试去访问父结点的右侧子结点------这个过程，和走迷宫是何其相似！事实上，在二叉树中，结点就好比是迷宫里的坐标，图中的每个结点在作为父结点时无疑是岔路口，而空结点就是死胡同。我们回顾一下二叉树先序遍历的编码实现：

js 复制代码

// 所有遍历函数的入参都是树的根结点对象
function preorder(root) {
    // 递归边界，root 为空
    if(!root) {
        return 
    }
     
    // 输出当前遍历的结点值
    console.log('当前遍历的结点值是：', root.val)  
    // 递归遍历左子树 
    preorder(root.left)  
    // 递归遍历右子树  
    preorder(root.right)
}

在这个递归函数中，递归式用来先后遍历左子树、右子树（分别探索不同的道路），递归边界在识别到结点为空时会直接返回（撞到了南墙）。因此，我们可以认为，递归式就是我们选择道路的过程，而递归边界就是死胡同。二叉树的先序遍历正是深度优先搜索思想的递归实现。可以说深度优先搜索过程就类似于树的先序遍历、是树的先序遍历的推广。

这时候，可能有同学会有疑问：在二叉树遍历的递归实现里，完全没有栈的影子------这东西似乎和栈没有什么直接联系啊，为啥咱们还说深度优先搜索的本质是栈呢？

我们从两个角度来理解这个事情：

首先，函数调用的底层，仍然是由栈来实现的。JS 会维护一个叫"函数调用栈"的东西，preorder每调用一次自己，相关调用的上下文就会被push进函数调用栈中；待函数执行完毕后，对应的上下文又会从调用栈中被pop出来。因此，即便二叉树的递归调用过程中，并没有出现栈这种数据结构，也依然改变不了递归的本质是栈的事实。
其次，DFS 作为一种思想，它和树的递归遍历一脉相承、却并不能完全地画上等号------DFS 的解题场景其实有很多，其中有一类会要求我们记录每一层递归式里路径的状态，此时就会强依赖栈结构（这一点会在下一节的真题实战中体现得淋漓尽致）。

基于上述的两个例子，相信大家已经对深度优先搜索的思想和实现思路形成了自己的理解。本节我们着重理解概念，不急着做题------深度优先搜索的应用是非常广泛的，在后续的小节中，大家自然会见到许许多多使用递归来实现深度优先搜索的实战案例。

广度优先搜索思想------找到迷宫出口的另一种思路

我们回头再来看看这个迷宫结构：

当我们使用深度优先搜索来寻找迷宫出口时，会走出图示这样一条一条的完整路径：

其中红色的圆点意味着路径的起点，红色箭头意味着路径的终点。我们看到从起点开始，一共探索出了 5 条完整的路径。

与深度优先搜索不同的是，广度优先搜索（BFS）并不执着于"一往无前"这件事情。它关心的是眼下自己能够直接到达的所有坐标，其动作有点类似于"扫描" ------比如说站在 B 这个岔路口，它会只关注 C、D、E 三个坐标，至于 F、G、H、I这些遥远的坐标，现在不在它的关心范围内：

只有在走到了 E处时，它发现此时可以触达的坐标变成了 F、G，此时才会去扫描F、G：

按照这个思路，广度优先搜索每次以"广度"为第一要务、雨露均沾，一层一层地扫描，最后也能够将所有的坐标扫描完全：

当扫描到 I 的时候，发现 I 是出口，照样能够找到答案。

按照 BFS 的遍历规则，具体的访问步骤会变成下面这样:

站在入口A处（第一层），发现直接能抵达的坐标只有B，于是接下来需要访问的就是 B。
入口A访问完毕，走到 B 处（第二层），发现直接能抵达的坐标变成了C、D和E，于是把这三个坐标记为下一层的访问对象。
B访问完毕，访问第三层。这里我按照从上到下的顺序（你也可以按照其它顺序），先访问 C和D，然后访问E。站在C处和D处都没有见到新的可以直接抵达的坐标，所以不做额外的动作。但是在E处见到了可以直接抵达的F和G，因此把F和G记为下一层（第四层）需要访问的对象。
第三层访问完毕，访问第四层。第四层按照从上到下的顺序，先访问的是 F。从F出发没有可以直接触达的坐标，因此不做额外的操作。接着访问G，发现从G出发可以直接抵达H和I，因此把H和I记为下一层（第五层）需要访问的对象。
第四层访问完毕，访问第五层。第五层按照从上到下的顺序，先访问的是H，发现从H出发没有可以直接抵达的坐标，因此不作额外的操作。接着访问I，发现I就是出口，问题得解。

当然啦，这个问题若采用 BFS 的思路来解，那么它其实已经不能说是一个严格的迷宫游戏了------在一个真正的迷宫游戏里，大概率并不会允许我们如此顺利地逐个访问身在同一层次的所有坐标（比如C和D之间可能就会隔了厚厚的一堵墙，导致你无法在访问C后直接去访问D）。这里我们基于迷宫游戏，抽象出来的其实是一个更为简单的模型。大家不必拘泥于游戏本身，而应该着重理解这个分层遍历的过程。

在分层遍历的过程中，大家会发现两个规律：

每访问完毕一个坐标，这个坐标在后续的遍历中都不会再被用到了，也就是说它可以被丢弃掉。
站在某个确定坐标的位置上，我们所观察到的可直接抵达的坐标，是需要被记录下来的，因为后续的遍历还要用到它们。

丢弃已访问的坐标、记录新观察到的坐标，这个顺序毫无疑问符合了"先进先出"的原则，因此整个 BFS 算法的实现过程，和队列有着密不可分的关系 。

下面我用一个队列 queue 来模拟一下上面的过程：

初始化，先将入口A入队（queue里现在只有A）。
访问入口A（第一层），访问完毕后将A出队。发现直接能抵达的坐标只有B，于是将B入队（queue里现在只有B）。
访问B（第二层），访问完毕后将B出队。发现直接能抵达的坐标变成了C、D和E，于是把这三个坐标记为下一层的访问对象，也就是把它们全部入队（queue里现在是C、D、E）
访问第三层。这里我按照从上到下的顺序（你也可以按照其它顺序），先访问 C（访问完毕后C出队）和D（访问完毕后D出队），然后访问E（访问完毕后E出队）。访问C处和D处都没有见到新的可以直接抵达的坐标，所以不做额外的动作。但是在E处我们见到了可以直接抵达的F和G，因此把F和G记为下一层（第四层）需要访问的对象，F、G依次入队（queue里现在是 F、G）。
访问第五层。第五层按照从上到下的顺序，先访问的是H（访问完毕后H出队），发现从H出发没有可以直接抵达的坐标，因此不作额外的操作。接着访问I（访问完毕后I出队），发现I就是出口，问题得解（此时 queue 队列已经被清空）。

在这个过程里，我们其实循环往复地做了以下事情：

依次访问队列里已经有的坐标，将其出队；记录从当前坐标出发可直接抵达的所有坐标，将其入队。

以上逻辑用伪代码表述如下：

js 复制代码

function BFS(入口坐标) {
    const queue = [] // 初始化队列queue
    // 入口坐标首先入队
    queue.push(入口坐标)
    // 队列不为空，说明没有遍历完全
    while(queue.length) {
        const top = queue[0] // 取出队头元素  
        
        访问 top // 此处是一些和 top 相关的逻辑，比如记录它对应的信息、检查它的属性等等
        
        // 注意这里也可以不用 for 循环，视题意而定
        for(检查 top 元素出发能够遍历到的所有元素)  {
            queue.push(top能够直接抵达的元素)
        }
        
        queue.shift() // 访问完毕。将队头元素出队
    }
}

注意，理论上来说只要我们拿到了 top，那么就不再关心队头元素了。因此这个 shift 出队的过程，其实是比较灵活的。一般只要我们拿到了 top，就可以执行 shift了。一些同学习惯于把top元素的访问和出队放在一起来做：

js 复制代码

const top = queue.shift()

这样做也是没问题的（除非题目中对出队的时机有强约束，但这种情况非常少见）。

BFS实战：二叉树的层序遍历

大家现在回顾一下我们在第 5 节展示过的这个二叉树实例：

这棵二叉树的编码实现如下：

js 复制代码

const root = {
  val: "A",
  left: {
    val: "B",
    left: {
      val: "D"
    },
    right: {
      val: "E"
    }
  },
  right: {
    val: "C",
    right: {
      val: "F"
    }
  }
};

现在我们要做的是对这个二叉树进行层序遍历。层序遍历的概念很好理解：按照层次的顺序，从上到下，从左到右地遍历一个二叉树，如图所示（红色数字即为遍历的序号）：

正确的遍历序列为：

css 复制代码

A
B
C
D
E
F

看到"层次"关键字，大家应该立刻想到"扫描"；想到"扫描"，就应该立刻想到 BFS。因此层序遍历，我们就用 BFS 的思路来实现。这里咱们可以直接套用上面的伪代码：

js 复制代码

function BFS(root) {
    const queue = [] // 初始化队列queue
    // 根结点首先入队
    queue.push(root)
    // 队列不为空，说明没有遍历完全
    while(queue.length) {
        const top = queue[0] // 取出队头元素  
        // 访问 top
        console.log(top.val)
        // 如果左子树存在，左子树入队
        if(top.left) {
            queue.push(top.left)
        }
        // 如果右子树存在，右子树入队
        if(top.right) {
            queue.push(top.right)
        }
        queue.shift() // 访问完毕，队头元素出队
    }
}

执行 BFS：

js 复制代码

BFS(root)

输出结果符合预期：

结语

经过本节的学习，相信大家对 DFS、BFS 的核心思想及实现方法都有了比较扎实的掌握。这两种算法在我们今后的做题过程中会反复出现，彼时大家会对它们的应用场景有更加深刻的认知。

（阅读过程中有任何想法或疑问，或者单纯希望和笔者交个朋友啥的，欢迎大家添加我的微信xyalinode与我交流哈~）

在开始之前

根据我深耕技术写作多年的经验，很多同学一看到标题里有"思想"两个字，就会觉得接下来要讲的一定是一个非常复杂的"高大上"理论，于是他会先给自己箍上一个"我一定学不会"的紧箍咒，接着心里就开始打退堂鼓了。这样的同学在和算法正面交锋之前，就先被自己内心的恐惧击垮了，实在可惜。

站在讲解者的角度来说，我确实不会先给大家画个饼，说这玩意儿有多么多么简单------这是一个非常不负责任的承诺。因为对于初学者来说，没有什么是简单的，从不会到会本来就是一个过程。况且，你现在学的是不少前端er都不肯学/学不动的算法，这本就不是一个轻松的挑战。但既然走到了这一步，不管你这会儿心里有多慌，我都希望你可以坚持一下、读读看，你会发现这玩意儿真的不是玄学------它真的很香。

如何学好这一节

不可否认，在一些传统教材里，谈及"思想"必定会有大段理论文字的堆砌，这也是很多同学学完数据结构直接放弃学习算法思想的重要原因。

但站在面试的角度来看，算法相关的考察几乎不存在"背知识点"这种形式，更多还是看你能不能把题做出来。算法思想是抽象的，题目却是具体的。我们常说"以题为纲"，其目的就是帮助大家站在具体去理解抽象。

本节我们先不用纠结什么是递归、什么是回溯，而是直接来做一道题，从题中去认识所谓的"思想"。

通过本节的学习，我希望大家能够认识到，"思想"并不是一坨剪不断理还乱、学了只能用来吹水的虚无概念。"思想"本质上就是套路，而且是普适性非常强的套路，它有着大量的对口问题。搞定了它，就搞定了一大波面试题------爽不爽？要想爽这一把，就不要轻易撤退。

关键套路初相见：全排列问题

题目描述：给定一个没有重复数字的序列，返回其所有可能的全排列。

示例：

输入: [1,2,3]

输出: [
$1,2,3\], \[1,3,2\], \[2,1,3\], \[2,3,1\], \[3,1,2\], \[3,2,1$
]

思路分析

"全排列"是高中数学里的一个概念，这里先带大家复习一下：

从n个不同元素中任取m（m≤n）个元素，按照一定的顺序排列起来，叫做从n个不同元素中取出m个元素的一个排列。当m=n时所有的排列情况叫全排列。

不过就算你已经完全忘了"全排列"到底是一个什么样的数学概念，也没有关系。结合题目描述和示例，我们依然可以分析出这道题想让我们做的事情：拿到一个 n 个数的数组作为入参，穷举出这 n 个数的所有排列方式。

哎？等等，我好像看到一个熟悉的词眼------穷举！楼上是不是说了穷举？我们最近还在哪里见过穷举？是不是在上一节？上一节的哪个位置？DFS 对不对？DFS 用什么实现比较好？递归！好，来得早不如来得巧，我现在就决定用递归来做这个题。

! 复制代码

如果你的脑回路暂时没有反应出来上面这些知识点之间的关联关系，也不要着急。新手上路，这很正常。    

做完下面一系列的题目之后，我会跟大家介绍这类题目的关键特征，到时候会有更直白的套路可以用。现在先不要慌，跟着我的思路往下走，好好敲代码

怎么做呢？大家仔细想想，在这个变化的序列中，不变的是什么------是不是坑位的数量？拿示例来说，不管我怎么调整数字的顺序，它们都只能围着这 3 个坑打转。当我们感到变化难以把握时，不如尝试先从不变的东西入手 。这里我把坑位给大家画出来：

现在问题变成了，我手里有 3 个数，要往这 3 个坑里填，有几种填法？我们一个一个坑来看：

Step1:：面对第一个坑，我有3种选择：填1、填2、填3，随机选择其中一个填进去即可。
Step2：面对第二个坑，由于 Step1 中已经分出去1个数字，现在只剩下2个选择：比如如果 Step1 中填进去的是 1，那么现在就剩下2、3；如果 Step1 中填进去的是 2，那么就剩下 1、3。
Step3：面对第三个坑，由于前面已经消耗了2个数字，此时我们手里只剩下 1 个数字了。所以说第 3 个坑是毫无悬念的，它只有1种可能。

我们把三个坑的情况统筹起来，那么全排列就一共有 3x2x1=6 种可能。可惜这道题问的不是全排列的可能性有多少种，而是要求你把每一种可能性都穷举出来。这其实有点类似于我们上一节玩迷宫游戏的时候，游戏规则不仅要求你回答出迷宫的通关方法有几种，还要求你列举出每一条路的路径。列举"路径"，我们首先要找到"坐标" 。在这道题里，"坐标"就是每一个坑里可能填进的数字。我把它画出来，你就明白了：

root 是一个空坐标，是我们分配数字的起点。

你可以想象自己此时此刻正手握 3 个数字站在 root 这个位置上。眼前是第一个坑，这个坑向你问道："小哥，你打算给我哪个数字呢？"

你说："不好说，这里有 3 种可能"。第一个坑里可以填的数字，对应的是以下三种情况：

接着，你走到了第二个坑。第二个坑问你："小哥，你打算给我哪个数字呢？"。

你仔细想想，说："不好说，这要看我给了 1 号坑哪个数字。但可以确定的是，不管我给了 1 号坑哪个数字，到你这里的时候，都只有 2 个数字可选了"。基于 1 号坑的分配结果，2 号坑分别有以下可能：

终于，你走到了第三个坑。此时，你手里只剩下 1 个数，还没等第 3 个坑问你要，你就对它说："哥，别挑了，我就剩一个了，你没得选"。说着，你把 1 号坑和 2 号坑挑完剩下的最后 1 个数给了 3 号坑：

有没有发现，不知不觉中，我们构造出了一个树结构。

从这个树结构里我们可以清晰地看出，全排列的所有可能性：

图中以圆点为起点，以箭头为终点，起点和终点之间就是一个完整的排列。

我们的思维路径是一个树结构，但这并不意味着我们需要真的在编码的时候去构造一棵树出来。回忆一下上一节，我们走迷宫的各种路径组合起来，是不是也是一个树结构？走迷宫时我们没有构造树，这里也不需要构造树。需要什么？需要递归！

即便不联想咱们刚刚学过的 DFS 知识点，这道题的解答思路中也有一个非常关键的特征在提醒你往递归去想，那就是重复。

! 复制代码

这里给大家一个思维工具：以后只要分析出重复的逻辑（排除掉类似数组遍历这种简单粗暴的重复），你都需要把递归从你的大脑内存里调度出来、将其列为"可以一试"的解法之一；只要想到递归，立刻回忆我们上一节讲的 DFS 思想、然后尝试套我们这一节末尾教给大家的解题模板。这个脑回路未必 100% 准确，但确实有极高的成功概率------题，是有规律的。这，就是规律之一。

在以上的"填坑"过程中，我们重复地做了以下事情：

检查手里剩下的数字有哪些
选取其中一个填进当前的坑里

在第 5 节初识递归时，大家已经知道"重复"的内容，就是递归式 。

这个重复递归式的动作一直持续到了最后一个数字也被填进坑里为止------"重复"的终点，就是递归边界 。

这里大家当然也可以借鉴遍历二叉树的经验，通过判断数组的可选数字是否为空，来决定当前是不是走到了递归边界。但是这道题其实可以做得更简单：坑位的个数是已知的，我们可以通过记录当前坑位的索引来判断是否已经走到了边界：比如说示例中有 n 个坑，假如我们把第 1 个坑的索引记为 0 ，那么索引为 n-1 的坑就是递归式的执行终点，索引为 n 的坑（压根不存在）就是递归边界。

递归的编码实现，无非是把我们上面描述过的递归式和递归边界翻译成代码：

编码实现

javascript 复制代码

/**
 * @param {number[]} nums
 * @return {number[][]}
 */
// 入参是一个数组
const permute = function(nums) {
  // 缓存数组的长度
  const len = nums.length
  // curr 变量用来记录当前的排列内容
  const curr = []
  // res 用来记录所有的排列顺序
  const res = []
  // visited 用来避免重复使用同一个数字
  const visited = {}
  // 定义 dfs 函数，入参是坑位的索引（从 0 计数）
  function dfs(nth) {
      // 若遍历到了不存在的坑位（第 len+1 个），则触碰递归边界返回
      if(nth === len) {
          // 此时前 len 个坑位已经填满，将对应的排列记录下来
          res.push(curr.slice())
          return 
      }
      // 检查手里剩下的数字有哪些
      for(let i=0;i<len;i++) {
          // 若 nums[i] 之前没被其它坑位用过，则可以理解为"这个数字剩下了"
          if(!visited[nums[i]]) {
              // 给 nums[i] 打个"已用过"的标
              visited[nums[i]] = 1
              // 将nums[i]推入当前排列
              curr.push(nums[i])
              // 基于这个排列继续往下一个坑走去
              dfs(nth+1) 
              // nums[i]让出当前坑位
              curr.pop()
              // 下掉"已用过"标识
              visited[nums[i]] = 0
          }
      }
  }
  // 从索引为 0 的坑位（也就是第一个坑位）开始 dfs
  dfs(0)
  return res
};

小贴士

上面这坨代码里，有两个点需要大家格外注意，它们将会成为我们以后做类似题目的关键技巧：

Map 结构 visited 的使用：填坑时，每用到一个数字，我们都要给这个数字打上"已用过"的标------避免它被使用第二次；数字让出坑位时，对应的排列和 visited 状态也需要被及时地更新掉。
当走到递归边界时，一个完整的排列也到手了。将这个完整排列推入结果数组时，我们用了 res.push(curr.slice()) 而不是简单的 res.push(curr) 。为什么这样做？因为全局只有一个唯一的 curr ， curr 的值会随着 dfs 的进行而不断被更新。 slice 方法的作用是帮助我们拷贝出一个不影响curr正本的副本，以防直接修改到curr的引用。

带着全排列问题教会我们的解题思路和编码技巧，我们再来看另一个类型的题目------组合问题。

组合问题：变化的"坑位"，不变的"套路"

题目描述：给定一组不含重复元素的整数数组 nums，返回该数组所有可能的子集（幂集）。

说明：解集不能包含重复的子集。
示例: 输入: nums = [1,2,3]

输出:
$\[3\], \[1\], \[2\], \[1,2,3\], \[1,3\], \[2,3\], \[1,2\], \[$
]

思路分析

见到这道题，大家第一反应会是什么？吸取了上一道题的经验，这道题我们应该想到的是：穷举出现了，大概率会用到 DFS 。

只要用到 DFS，就不得不想到树形思维方式 ，进而不得不思考递归式和递归边界的问题。在这个思考的过程中，最重要的一环就是对"坑位"的定位和分析。

从上一道题中，我们不难看出，"坑位"对应的就是树形逻辑中树的某一层，"坑位数"往往意味着递归边界的限制条件。

找"坑位"的思路也是具有规律的："坑位"往往是那些不会变化的东西。在上一道题中，排列的顺序是变化的，而每个排列中数字的个数却是不变的，因此数字的个数就对应"坑位"的个数；在这道题中，每个组合中数字的个数是不确定的，不变的东西变成了可以参与组合的数字 ，变化的东西则是每个数字在组合中的存在性 。因此我们的思路可以调整为，从每一个数字入手，讨论它出现或者不出现的情况。

换汤不换药，这里我们仍然采取树形思维模型：

为了使存在性凸显得更具体，这里我直接把树形结构中每一层对应的可能组合给大家列出来：

javascript 复制代码

root                                            []                  
数字1------第一层                     1                                   []
数字2------第二层            [1,2]            [1]                   [2]         []
数字3---------第三层    [1,2,3]     [1,2]  [1,3]   [1]           [2,3]   [2]   [3]  []

从 root 出发，每一个数字对应树的一层，存在或不存在对应树的两个分叉 。从第一层到第三层，我们得到的所有完整路径，就是 3 个数的所有可能的组合形式。

我们分析一下这个过程中的递归式与递归边界：

递归式：检查手里剩下的数字有哪些（有没有发现和上一道题的递归式是一样的，因为两道题都强调了数字不能重复使用），选取其中一个填进当前的坑里、或者干脆把这个坑空出来（这里就体现出了和上一道题的区别，这道题强调的是存在性而非顺序）。
递归边界：组合里数字个数的最大值。拿示例来说，只给了 3 个数，因此组合里数字最多也只有 3 个，超过 3 个则视为触碰递归边界。

按照这个思路，可以编码如下：

编码实现

javascript 复制代码

/**
 * @param {number[]} nums
 * @return {number[][]}
 */
// 入参是一个数组
const subsets = function(nums) {
    // 初始化结果数组
    const res = []   
    // 缓存数组长度
    const len = nums.length
    // 初始化组合数组
    const subset = []
    // 进入 dfs
    dfs(0)  

    // 定义 dfs 函数，入参是 nums 中的数字索引
    function dfs(index) {
        // 每次进入，都意味着组合内容更新了一次，故直接推入结果数组
        res.push(subset.slice())
        // 从当前数字的索引开始，遍历 nums
        for(let i=index;i<len;i++) {
            // 这是当前数字存在于组合中的情况
            subset.push(nums[i]) 
            // 基于当前数字存在于组合中的情况，进一步 dfs
            dfs(i+1)
            // 这是当前数字不存在与组合中的情况
            subset.pop()
        }
    }
    // 返回结果数组
    return res 
};

编码复盘

这道题和上一道题的基本思路高度一致，但是在实现上有些差别。对初学者来说，即便是非常微小的变化也有可能引起困惑。因此，我在这里针对编码部分变化的内容作进一步讲解：

递归式的变化：在上一道题中，我们检查一个数字是否可用的依据是它是否已被纳入当前排列（ visited 值是否为 1），而这道题中，并不存在一个类似 visited 一样的标记对象。取而代之的，是每次直接以 index 作为了索引起点。这是因为，在排列场景下，一个元素可能出现在任何坑位里；而在组合场景下，坑位的选择逻辑发生了变化，坑位和元素是一一对应的。因此讨论完一个坑位的取舍后，一个元素的取舍也相应地讨论完毕了，直接跳过这个元素的索引往下走即可。
递归边界的变化：这道题中，并没有显式的 return 语句来标示递归边界的存在。这个边界的判定被 for 语句偷偷地做掉了： for 语句会遍历所有的数字，当数字遍历完全时，也就意味着递归走到了尽头。

限定组合问题：及时回溯，即为"剪枝"

题目描述：给定两个整数 n 和 k，返回 1 ... n 中所有可能的 k 个数的组合。
示例: 输入: n = 4, k = 2

输出:
$\[2,4\], \[3,4\], \[2,3\], \[1,2\], \[1,3\], \[1,4\],$

思路分析

这是一道复杂化的组合问题，它追加了一个限定条件------只返回 n 个数中 k 个数的组合。在普通的组合问题中，树形逻辑是这样的：

而在这道题里，树形逻辑被"截胡"了，它要求我们只输出其中的一部分。假如 n=3， k=2，那么需要输出的内容就如下图的红色箭头所示：

我们发现，只有双向箭头所指的结点组合被认为是有效结果，其它结点都被丢弃了。在寻找这三对结点组合的过程中，我们一旦找到一对，就停止继续往深处搜索，这就意味着一些结点压根没有机会被遍历到。

这其实就是"剪枝"的过程------在深度优先搜索中，有时我们会去掉一些不符合题目要求的、没有作用的答案，进而得到正确答案。这个丢掉答案的过程，形似剪掉树的枝叶，所以这一方法被称为"剪枝" 。

在这道题中，要做到剪枝，我们需要分别在组合问题的递归式和递归边界上动手脚：

递归式：普通组合问题，每到一个新的坑位处，我们都需要对组合结果数组进行更新；这道题中，当且仅当组合内数字个数为 k 个时，才会对组合结果数组进行更新。
递归边界：只要组合内数字个数达到了 k 个，就不再继续当前的路径往下遍历，而是直接返回。

基于这两个改造点，我们可以编码如下：

编码实现

javascript 复制代码

/**
 * @param {number} n
 * @param {number} k
 * @return {number[][]}
 */
const combine = function(n, k) {
   // 初始化结果数组
    const res = []   
    // 初始化组合数组
    const subset = []
    // 进入 dfs，起始数字是1
    dfs(1)  

    // 定义 dfs 函数，入参是当前遍历到的数字
    function dfs(index) {
        if(subset.length === k) {
            res.push(subset.slice())
            return 
        }
        // 从当前数字的值开始，遍历 index-n 之间的所有数字
        for(let i=index;i<=n;i++) {
            // 这是当前数字存在于组合中的情况
            subset.push(i) 
            // 基于当前数字存在于组合中的情况，进一步 dfs
            dfs(i+1)
            // 这是当前数字不存在与组合中的情况
            subset.pop()
        }
    }
    // 返回结果数组
    return res 
};

注意这道题中虽然没有直接给出一个 nums 数组，而是直接约定了数字的范围为 1-n ，但其本质仍然是一个数字集合，我们像上面这样稍微调整下取值方式即可。

概念复盘：何为"回溯"？

现在，或许你还暂时不知道何为"回溯算法"，但你其实已经实打实地在真题中对它有了具体的实践。基于这些实践，我们反过来理解一下回溯的概念：

回溯算法实际上一个类似枚举的搜索尝试过程，主要是在搜索尝试过程中寻找问题的解，当发现已不满足求解条件时，就 "回溯" 返回，尝试别的路径。

回溯法是一种选优搜索法，按选优条件向前搜索，以达到目标。但当探索到某一步时，发现原先选择并不优或达不到目标，就退回一步重新选择，这种走不通就退回再走的技术为回溯法，而满足回溯条件的某个状态的点称为 "回溯点"。

许多复杂的，规模较大的问题都可以使用回溯法，有"通用解题方法"的美称。

回溯算法的基本思想是：从一条路往前走，能进则进，不能进则退回来，换一条路再试。 ------LeetCode

我们重点关注这句话："回溯算法的基本思想是：从一条路往前走，能进则进，不能进则退回来，换一条路再试。"

有没有发现，这个"回溯算法"和上一节的 DFS ，好像翻来覆去是在讲同一件事情？

实际上，这里的"回溯"二字，大家可以理解为是在强调 DFS 过程中"退一步重新选择"这个动作。这样想的话， DFS 算法其实就是回溯思想的体现。

这里顺便给大家提个醒：一些同学在平时的刷题和面试中，会因为对"回溯"的定义感到困惑，进而拼命地钻牛角尖，这样的做法是非常不可取的。

早年笔者有过一段短暂的 ACMer 生涯，彼时关于回溯，老师曾经给出过一个这样的解读："在我们接下来要应对的题目里，有递归就会有回溯。回溯算法的特别之处，在于其对应的题目往往要求你在递归过程中求出一个确切的解"。后来笔者自己乱七八糟地读了一堆算法相关的"名著"，其中又有一本书这样定义回溯："涉及剪枝操作的递归，我们一般称之为回溯"。

大家会发现，关于回溯算法的定义，可以说是仁者见仁、智者见智。这也是我不建议大家从概念入手去学算法的一个原因------反复纠结文字游戏，无法给你带来任何实质上的能力提升。在实际面试中，没有一个面试官会要求你默写算法的定义，他关注的一定是你的解题思路和编码内容------什么都是浮云，能把题做出来，才是王道！

递归与回溯问题------解题模板总结

做完了楼上三道典型例题，相信大家此时都有了一些微妙的感觉------这三道题的解题方法是非常相似的，是不是意味着涉及递归回溯、或者说涉及 DFS 应用的题目，都有某种共通之处呢？会不会存在某种解题套路，可以帮助我们知一解百、举一反 N 呢？

能想到这一层的老铁，我要给你双击一个巨大的 666------善于总结，积极寻找题目与题目之间的关联，尝试发掘题目中反映出来的规律，这都是非常棒的学习习惯。

对于递归回溯系列的问题，笔者自己在刷题过程中总结出了一套模板。在这套模板的引导下，笔者至今还没有在递归回溯问题上翻过车。在这里我和大家分享这套模板，同时也希望各位在身经百战之后，能够针对不同类型的问题，尝试去总结一套属于你自己的解题模板。

如何总结出一套解题模板？其实很简单，大家只需要搞清楚三个问题：

什么时候用？（明确场景）
为什么这样用？（提供依据）
怎么用？（细化步骤）

拿这个专题来说，我给出的解题模板内容如下：

什么时候用

看两个特征：

题目中暗示了一个或多个解，并且要求我们详尽地列举出每一个解的内容时，一定要想到 DFS、想到递归回溯。
题目经分析后，可以转化为树形逻辑模型求解。

为什么这样用

递归与回溯的过程，本身就是穷举的过程。题目中要求我们列举每一个解的内容，解从哪来？解是基于穷举思想、对搜索树进行恰当地剪枝后得来的。

! 复制代码

这里需要大家注意到另一种问法：不问解的内容，只问解的个数。这类问题往往不用 DFS 来解，而是用动态规划（我们后面会学）。这里，大家先记下这个辨析，对以后做题会有帮助。

怎么用

一个模型------树形逻辑模型；两个要点------递归式和递归边界。

树形逻辑模型的构建，关键在于找"坑位"，一个坑位就对应树中的一层，每一层的处理逻辑往往是一样的，这个逻辑就是递归式的内容。至于递归边界，要么在题目中约束得非常清楚、要么默认为"坑位"数量的边界。

用伪代码总结一下编码形式，大部分的题解都符合以下特征：

javascript 复制代码

function xxx(入参) {
  前期的变量定义、缓存等准备工作 
  
  // 定义路径栈
  const path = []
  
  // 进入 dfs
  dfs(起点) 
  
  // 定义 dfs
  dfs(递归参数) {
    if(到达了递归边界) {
      结合题意处理边界逻辑，往往和 path 内容有关
      return   
    }
    
    // 注意这里也可能不是 for，视题意决定
    for(遍历坑位的可选值) {
      path.push(当前选中值)
      处理坑位本身的相关逻辑
      path.pop()
    }
  }
}

在面试中，如果你隐约觉得这道题用递归回溯来解可能有戏，却一时间没办法明确具体的解法，那么不妨尝试把这段伪代码记在脑子里。在面试时，先把框架写出来，然后结合题意去调整和填充伪代码的内容------很多时候，我们做题缺的不是知识储备，而是一个具体的切入点。

（阅读过程中有任何想法或疑问，或者单纯希望和笔者交个朋友啥的，欢迎大家添加我的微信xyalinode与我交流哈~）

二叉树在面试实战中，花样非常多。本节只是个开头，在后面几个专题、包括最后的大厂真题实战环节中，我们都不会停止对二叉树相关考点的学习和探讨。

在本节，有以下三个命题方向需要大家重点掌握：

迭代法实现二叉树的先、中、后序遍历
二叉树层序遍历的衍生问题
翻转二叉树

这三个方向对应的考题都比较经典。与此同时，解决这些问题涉及到的思路和编码细节，也会成为各位日后解决更加复杂的问题的基石。因此，虽然本节篇幅略长，但还是希望各位能够倾注耐心，给自己充分的时间去理解和消化这些知识。

"遍历三兄弟"的迭代实现

经过第5节的学习，相信各位已经将二叉树先、中、后序遍历的递归实现吃得透透的了。在使用递归实现遍历的过程中，我们明显察觉到，"遍历三兄弟"的编码实现也宛如孪生兄弟一样，彼此之间只有代码顺序上的不同，整体内容基本是一致的。这正是递归思想的一个重要的优点------简单。

这里的"简单"并不是说学起来简单。相反，结合笔者早期的读者调研来看，大部分同学都认为递归学起来让人很难受（这也是正常的）。

初学递归的人排斥递归，大部分是出于对"函数调用自身"这种骚操作的不适应。但只要你能克服这种不适应，并且通过反复的演练去吸收这种解题方法，你就会发现递归真的是个好东西。因为通过使用递归，我们可以把原本复杂的东西，拆解成非常简单的、符合人类惯用脑回路的逻辑。

这样说可能还是有点抽象，不过没关系，接下来我会讲解"遍历三兄弟"对应的迭代解法。等我们学完这坨东西之后，心怀疑惑的同学不妨拿迭代法的代码和第5节中递归法的代码比较一下，相信你会毫不犹豫地回头对递归说上一句"真香！"。

从先序遍历说起

题目描述：给定一个二叉树，返回它的前序（先序）遍历序列。
示例: 输入: [1,null,2,3]

复制代码

输出: [1,2,3]

进阶: 递归算法很简单，你可以通过迭代算法完成吗？

思路分析

注意最后那一行小字："递归算法很简单，你可以通过迭代算法完成吗？"，对递归算法有疑问的同学，趁这个机会赶紧复习下第五小节，本节我们只讲迭代法。

前面两个小节，我们一直在强调，递归和栈有着脱不开的干系。当一道本可以用递归做出来的题，突然不许你用递归了，此时我们本能的反应，就应该是往栈上想。

在基于栈来解决掉这个题之前，我要先跟平时用 leetcode 刷题的各位强调一个常识。

现在大家回头看这道题目给我们的输入和输出：输入看似是一个数组，实则不是。大家谨记，二叉树题目的输入只要没有额外强调，那么一般来说它都是基于这样的一个对象结构嵌套而来的：

javascript 复制代码

function TreeNode(val) {
    this.val = val;
    this.left = this.right = null;
}

比如这样：

javascript 复制代码

const root = {
  val: "A",
  left: {
    val: "B",
    left: {
      val: "D"
    },
    right: {
      val: "E"
    }
  },
  right: {
    val: "C",
    right: {
      val: "F"
    }
  }
};

话说回来，为啥题上给的不是对象，而是这样的一个数组呢：

javascript 复制代码

[1,null,2,3]

这其实是一种简化的写法，性质跟咱们写伪代码差不多。它的作用主要是描述二叉树的值，至于二叉树的结构，我们以题中给出的树形结构为准：

javascript 复制代码

OK，了解了输入内容，现在再来看输出：

javascript 复制代码

[1,2,3]

这里这个输出就简单多了，它是一个真数组 。为什么可以判断它是一个真数组呢？因为题目中要求你输出的是一个遍历序列，而不是一个二叉树。因此大家最后需要塞入结果数组的不是结点对象，而是结点的值。

! 复制代码

注意：       
以上的出参入参规律，是针对 leetcode 及其周边 OJ 来说的。OJ 中这样编写题目描述，是情理之中，因为 OJ 本身是支持多语言的，它只能对最通用的一部分信息进行透出。在面试场景下，不排除一些公司可能会贴心地把 JS 版本的出参和入参给出来，但更多的还是会直接复制粘贴 leetcode 或者其它一些算法书中的原题。如果你对题目的出参和入参有疑问，请大胆地对面试官说出你的困惑------没有一个正常面试官会在题目描述上为难你， 他比你更急切地想看到你刷刷写代码的英姿。

回到题目上来。我们接着栈往下说，题目中的出参是一个数组，大家仔细看这个数组，它像不像是一个栈的出栈序列？实际上，做这道题的一个根本思路，就是通过合理地安排入栈和出栈的时机、使栈的出栈序列符合二叉树的前序遍历规则 。

前序遍历的规则是，先遍历根结点、然后遍历左孩子、最后遍历右孩子------这正是我们所期望的出栈序列。按道理，入栈序列和出栈序列相反，我们似乎应该按照 右->左->根 这样的顺序将结点入栈。不过需要注意的是，我们遍历的起点就是根结点，难道我们要假装没看到这个根结点、一鼓作气找到最右侧结点之后才开始进行入栈操作吗？答案当然是否定的，我们的出入栈顺序应该是这样的：

将根结点入栈
取出栈顶结点，将结点值 push 进结果数组
若栈顶结点有右孩子，则将右孩子入栈
若栈顶结点有左孩子，则将左孩子入栈

这整个过程，本质上是将当前子树的根结点入栈、出栈，随后再将其对应左右子树入栈、出栈的过程。

重复 2、3、4 步骤，直至栈空，我们就能得到一个先序遍历序列。

编码实现

javascript 复制代码

/**
 * @param {TreeNode} root
 * @return {number[]}
 */
const preorderTraversal = function(root) {
  // 定义结果数组
  const res = []  
  // 处理边界条件
  if(!root) {
      return res
  }
  // 初始化栈结构
  const stack = [] 
  // 首先将根结点入栈
  stack.push(root)  
  // 若栈不为空，则重复出栈、入栈操作
  while(stack.length) {
      // 将栈顶结点记为当前结点
      const cur = stack.pop() 
      // 当前结点就是当前子树的根结点，把这个结点放在结果数组的尾部
      res.push(cur.val)
      // 若当前子树根结点有右孩子，则将右孩子入栈
      if(cur.right) {
          stack.push(cur.right)
      }
      // 若当前子树根结点有左孩子，则将左孩子入栈
      if(cur.left) {
          stack.push(cur.left)
      }
  }
  // 返回结果数组
  return res
};

异曲同工的后序遍历迭代实现

思路分析

后序遍历的出栈序列，按照规则应该是 左 -> 右 -> 根 。这个顺序相对于先序遍历，最明显的变化就是根结点的位置从第一个变成了倒数第一个。

如何做到这一点呢？与其从 stack 这个栈结构上入手，不如从 res 结果数组上入手：我们可以直接把 pop 出来的当前结点 unshift 进 res 的头部，改造后的代码会变成这样：

javascript 复制代码

while(stack.length) {
  // 将栈顶结点记为当前结点
  const cur = stack.pop() 
  // 当前结点就是当前子树的根结点，把这个结点放在结果数组的头部
  res.unshift(cur.val)
  // 若当前子树根结点有右孩子，则将右孩子入栈
  if(cur.right) {
    stack.push(cur.right)
  }
  // 若当前子树根结点有左孩子，则将左孩子入栈
  if(cur.left) {
    stack.push(cur.left)
  }
}

大家可以尝试在大脑里预判一下这个代码的执行顺序：由于我们填充 res 结果数组的顺序是从后往前填充（每次增加一个头部元素），因此先出栈的结点反而会位于 res 数组相对靠后的位置。出栈的顺序是 当前结点 -> 当前结点的左孩子 -> 当前结点的右孩子 ，其对应的 res 序列顺序就是 右 -> 左 -> 根 。这样一来，根结点就成功地被我们转移到了遍历序列的最末尾。

现在唯一让人看不顺眼的只剩下这个右孩子和左孩子的顺序了，这两个孩子结点进入结果数组的顺序与其被 pop 出栈的顺序是一致的，而出栈顺序又完全由入栈顺序决定，因此只需要相应地调整两个结点的入栈顺序就好了：

javascript 复制代码

// 若当前子树根结点有左孩子，则将左孩子入栈
if(cur.left) {
  stack.push(cur.left)
}  
// 若当前子树根结点有右孩子，则将右孩子入栈
if(cur.right) {
  stack.push(cur.right)
}

如此一来，右孩子就会相对于左孩子优先出栈，进而被放在 res 结果数组相对靠后的位置， 左 -> 右 ->根 的排序规则就稳稳地实现出来了。

我们把以上两个改造点结合一下，就有了以下代码：

编码实现

javascript 复制代码

/**
 * @param {TreeNode} root
 * @return {number[]}
 */
const postorderTraversal = function(root) {
  // 定义结果数组
  const res = []  
  // 处理边界条件
  if(!root) {
      return res
  }
  // 初始化栈结构
  const stack = [] 
  // 首先将根结点入栈
  stack.push(root)  
  // 若栈不为空，则重复出栈、入栈操作
  while(stack.length) {
      // 将栈顶结点记为当前结点
      const cur = stack.pop() 
      // 当前结点就是当前子树的根结点，把这个结点放在结果数组的头部
      res.unshift(cur.val)
      // 若当前子树根结点有左孩子，则将左孩子入栈
      if(cur.left) {
        stack.push(cur.left)
      }  
      // 若当前子树根结点有右孩子，则将右孩子入栈
      if(cur.right) {
        stack.push(cur.right)
      }
  }
  // 返回结果数组
  return res
};

思路清奇的中序遍历迭代实现

思路分析

经过上面的讲解，大家会发现先序遍历和后序遍历的编码实现其实是非常相似的，它们遵循的都是同一套基本框架。那么我们能否通过对这个基本框架进行微调、从而同样轻松地实现中序遍历呢？

答案是不能，为啥不能？因为先序遍历和后序遍历之所以可以用同一套代码框架来实现，本质上是因为两者的出栈、入栈逻辑差别不大------都是先处理根结点，然后处理孩子结点。而中序遍历中，根结点不再出现在遍历序列的边界、而是出现在遍历序列的中间。这就意味着无论如何我们不能再将根结点作为第一个被 pop 出来的元素来处理了------出栈的时机被改变了，这意味着入栈的逻辑也需要调整。这一次我们不能再通过对 res 动手脚来解决问题，而是需要和 stack 面对面 battle。

中序遍历的序列规则是 左 -> 中 -> 右 ，这意味着我们必须首先定位到最左的叶子结点。在这个定位的过程中，必然会途径目标结点的父结点、爷爷结点和各种辈分的祖宗结点：

途径过的每一个结点，我们都要及时地把它入栈。这样当最左的叶子结点出栈时，第一个回溯到的就是它的父结点：

有了父结点，就不愁找不到兄弟结点，遍历结果就变得唾手可得了~

基于这个思路，我们来写代码：

编码实现

javascript 复制代码

/**
 * @param {TreeNode} root
 * @return {number[]}
 */
const inorderTraversal = function(root) {
  // 定义结果数组
  const res = []  
  // 初始化栈结构
  const stack = []   
  // 用一个 cur 结点充当游标
  let cur = root  
  // 当 cur 不为空、或者 stack 不为空时，重复以下逻辑
  while(cur || stack.length) {
      // 这个 while 的作用是把寻找最左叶子结点的过程中，途径的所有结点都记录下来 
      while(cur) {
          // 将途径的结点入栈
          stack.push(cur)  
          // 继续搜索当前结点的左孩子
          cur = cur.left  
      }
      // 取出栈顶元素
      cur = stack.pop()  
      // 将栈顶元素入栈
      res.push(cur.val)  
      // 尝试读取 cur 结点的右孩子
      cur = cur.right
  }
  // 返回结果数组
  return res
};

编码复盘

读完这段编码示范，一部分同学可能已经开始懵逼了：看着前面给出的思路分析，似乎完全写不出上面这样的代码啊！所以这段代码到底在干嘛？？？

如果你没有这样的困惑，说明你是一位悟性比较高的同学，可以直接跳过编码复盘部分往下读了（btw给你点个赞~）。

实不相瞒，如果你是初学者，这段代码可能确实需要大家在脑内反复运行、反复跑 demo 才能理解其中的逻辑。为了加快这个过程，我把其中看上去稍微拐弯抹角一点的逻辑摘出来，给大家点拨一下：

两个 while ：内层的 while 的作用是在寻找最左叶子结点的过程中，把途径的所有结点都记录到 stack 里。记录工作完成后，才会走到外层 while 的剩余逻辑里------这部分逻辑的作用是从最左的叶子结点开始，一层层回溯遍历左孩子的父结点和右侧兄弟结点，进而完成整个中序遍历任务。
外层 while 的两个条件： cur 的存在性和stack.length 的存在性，各自是为了限制什么？
1. stack.length 的存在性比较好理解， stack 中存储的是没有被推入结果数组 res 的待遍历元素。只要 stack 不为空，就意味着遍历没有结束，遍历动作需要继续重复。
2. cur 的存在性就比较有趣了。它对应以下几种情况：
  1. 初始态， cur 指向 root 结点，只要 root 不为空， cur 就不为空。此时判断了 cur 存在后，就会开始最左叶子结点的寻找之旅。这趟"一路向左"的旅途中， cur 始终指向当前遍历到的左孩子。
  2. 第一波内层 while 循环结束， cur 开始承担中序遍历的遍历游标职责。 cur 始终会指向当前栈的栈顶元素，也就是"一路向左"过程中途径的某个左孩子，然后将这个左孩子作为中序遍历的第一个结果元素纳入结果数组。假如这个左孩子是一个叶子结点，那么尝试取其右孩子时就只能取到 null ，这个 null 的存在，会导致内层循环 while 被跳过，接着就直接回溯到了这个左孩子的父结点，符合 左->根 的序列规则
  3. 假如当前取到的栈顶元素不是叶子结点，同时有一个右孩子，那么尝试取其右孩子时就会取到一个存在的结点。 cur 存在，于是进入内层 while 循环，重复"一路向左"的操作，去寻找这个右孩子对应的子树里最靠左的结点，然后去重复刚刚这个或回溯、或"一路向左"的过程。如果这个右孩子对应的子树里没有左孩子，那么跳出内层 while 循环之后，紧接着被纳入 res 结果数组的就是这个右孩子本身，符合 根->右 的序列规则

结合上面的分析，大家会不会觉得中序遍历迭代法的这一通操作非常奇妙呢？短短的几行代码，里面竟然藏着这么广阔的乾坤，牛x、牛x。

作为初学者，即便第一次写不出来上面的解法，也没什么好丧气的------大家谨记，关于二叉树的先、中、后序遍历，你对自己的要求应该是能够默写，也就是说要对上面这些逻辑充分熟悉、深刻记忆 。

在熟悉和记忆的过程中，你会渐渐地对这些乍一看似乎很巧妙的操作产生一种"这也很自然嘛"的感觉，这种感觉就意味着你对这个思路的充分吸收。还是那句话，千万不要以为理解就是终点，你需要做的是记忆！记忆！理解是一种感觉，记忆却能保证你在做题时一秒钟映射到具体的套路和代码------只有靠自己的双手写出来的代码，才是最可靠的伙伴。

层序遍历的衍生问题

在 DFS 和 BFS 这一节，我们已经讲过了二叉树层序遍历的实现方法。层序遍历本本身难度不大，但一想到这是一个关键考点，出题这帮人就每天绞尽脑汁地想要把简单的问题复杂化。于是，就有了我们眼下这个命题方向------层序遍历的衍生问题。

对于这类问题，我们接下来会讲最有代表性的一道作为例题。各位只要能吃透这一道的基本思路，就能够轻松地在类似的变体中举一反三（例题请大家好好把握，在大厂真题训练环节，我会给出一道变体来检验各位的学习效果）。

题目描述：给你一个二叉树，请你返回其按层序遍历得到的节点值。（即逐层地，从左到右访问所有节点）。
示例：二叉树：[3,9,20,null,null,15,7],

复制代码

返回其层次遍历结果：
$\[3\], \[9,20\], \[15,7$
]

思路分析

层序遍历没有那么多幺蛾子，大家看到层序遍历就应该条件反射出 BFS+队列 这对好基友。所谓变体，不过是在 BFS 的过程中围绕结果数组的内容做文章。

拿这道题来说，相对于我们 14 节中讲过的层序遍历基本思路，它变出的花样仅仅在于要求我们对层序遍历结果进行分层。也就是说只要我们能在 BFS 的过程中感知到当前层级、同时用不同的数组把不同的层级区分开，这道题就得解了。

如何做到这一点？大家需要知道一个非常重要的信息：我们在对二叉树进行层序遍历时，每一次 while 循环其实都对应着二叉树的某一层。只要我们在进入while循环之初，记录下这一层结点个数，然后将这个数量范围内的元素 push 进同一个数组，就能够实现二叉树的分层。

编码实现

javascript 复制代码

/**
 * @param {TreeNode} root
 * @return {number[][]}
 */
const levelOrder = function(root) {
    // 初始化结果数组
    const res = []  
    // 处理边界条件
    if(!root) {
        return res
    }  
    // 初始化队列
    const queue = []   
    // 队列第一个元素是根结点
    queue.push(root)  
    // 当队列不为空时，反复执行以下逻辑
    while(queue.length) {
        // level 用来存储当前层的结点
        const level = []  
        // 缓存刚进入循环时的队列长度，这一步很关键，因为队列长度后面会发生改变
        const len = queue.length  
        // 循环遍历当前层级的结点
        for(let i=0;i<len;i++) {
            // 取出队列的头部元素
            const top = queue.shift()  
            // 将头部元素的值推入 level 数组
            level.push(top.val)
            // 如果当前结点有左孩子，则推入下一层级
            if(top.left) {
                queue.push(top.left)
            }
            // 如果当前结点有右孩子，则推入下一层级
            if(top.right) {
                queue.push(top.right)
            }
        }
        // 将 level 推入结果数组
        res.push(level)
    }
    // 返回结果数组
    return res
};

翻转二叉树

翻转二叉树是一个非常经典的问题。之前有一个关于这道题的笑话，说是Homebrew的作者去面 Google，结果因为不会翻转二叉树被挂掉了。Google 在给这位大佬的拒信中写道：

我们90％的工程师使用您编写的软件(Homebrew)，但是您却无法在面试时在白板上写出翻转二叉树这道题，这太糟糕了。

这个故事之所以是个笑话，是因为翻转二叉树在算法面试中实在太常见了------只要你准备算法面试，你就不得不做这个题。在面试中做不出这道题的同学，会给面试官留下基础不牢的糟糕印象。

接下来我们就一起来搞定这道翻转二叉树，成为比homebrew作者更懂算法面试的人（逃

题目描述：翻转一棵二叉树。
示例：

输入：

markdown 复制代码

     4
   /   \
  2     7
 / \   / \
1   3 6   9

输出：

markdown 复制代码

     4
   /   \
  7     2
 / \   / \
9   6 3   1

思路分析

这道题是一道非常经典的递归应用题。

一棵二叉树，经过翻转后会有什么特点？答案是每一棵子树的左孩子和右孩子都发生了交换。既然是"每一棵子树"，那么就意味着重复，既然涉及了重复，就没有理由不用递归。

于是这道题解题思路就非常明确了：以递归的方式，遍历树中的每一个结点，并将每一个结点的左右孩子进行交换。

编码实现

js 复制代码

/**
 * @param {TreeNode} root
 * @return {TreeNode}
 */
const invertTree = function(root) {
    // 定义递归边界
    if(!root) {
        return root;
    }
    // 递归交换右孩子的子结点
    let right = invertTree(root.right);
    // 递归交换左孩子的子结点
    let left = invertTree(root.left);
    // 交换当前遍历到的两个左右孩子结点
    root.left = right;
    root.right = left;
    return root;
};

（阅读过程中有任何想法或疑问，或者单纯希望和笔者交个朋友啥的，欢迎大家添加我的微信xyalinode与我交流哈~）二叉搜索树（Binary Search Tree）简称 BST，是二叉树的一种特殊形式。它有很多别名，比如排序二叉树、二叉查找树等等。

虽然二叉搜索树多年来一直作为算法面试的"必要考点"存在，但在实际面试中，它的考察频率并不能和常规二叉树相提并论，算不上"大热"的考点，同时考察内容也是相对比较稳定的。对于二叉搜索树，我们只要能够把握好它的限制条件和特性，就足以应对大部分的考题。

什么是二叉搜索树

树的定义总是以递归的形式出现，二叉搜索树也不例外，它的递归定义如下：

是一棵空树
是一棵由根结点、左子树、右子树组成的树，同时左子树和右子树都是二叉搜索树，且左子树 上所有结点的数据域都小于等于 根结点的数据域，右子树 上所有结点的数据域都大于等于根结点的数据域

满足以上两个条件之一的二叉树，就是二叉搜索树。

从这个定义我们可以看出，二叉搜索树强调的是数据域的有序性 。也就是说，二叉搜索树上的每一棵子树，都应该满足 左孩子 <= 根结点 <= 右孩子 这样的大小关系。下图我给出了几个二叉搜索树的示例：

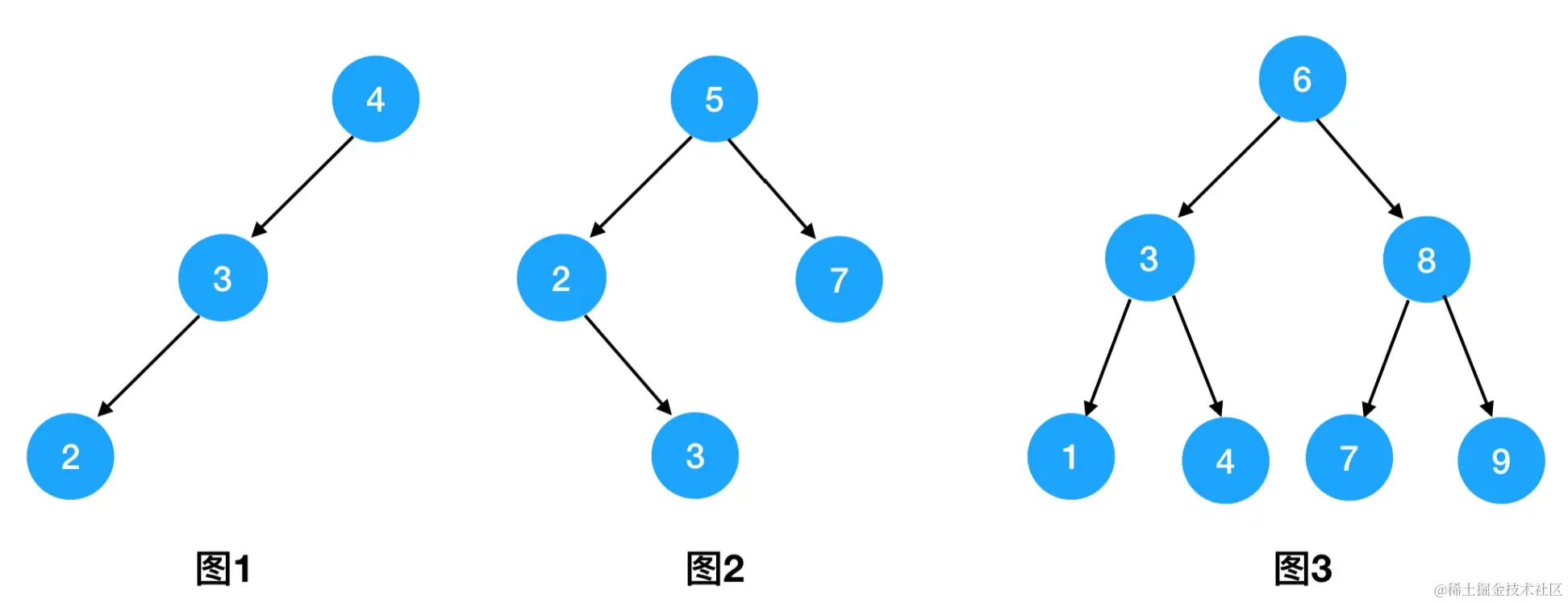以第三棵树为例，根结点的数据域为6，它的左子树的所有结点都小于等于6、右子树的所有结点都大于等于6。同时在任意子树的内部，也满足这个条件------比如左子树中，根结点值为3，根结点对应左子树的所有结点都小于等于3、右子树的所有结点都大于等于3。

二叉搜索树：编码基本功

关于二叉搜索树，大家需要掌握以下高频操作：

查找数据域为某一特定值的结点
插入新结点
删除指定结点

查找数据域为某一特定值的结点

假设这个目标结点的数据域值为 n，我们借助二叉搜索树数据域的有序性，可以有以下查找思路：

递归遍历二叉树，若当前遍历到的结点为空，就意味着没找到目标结点，直接返回。
若当前遍历到的结点对应的数据域值刚好等于n，则查找成功，返回。
若当前遍历到的结点对应的数据域值大于目标值n，则应该在左子树里进一步查找，设置下一步的遍历范围为 root.left 后，继续递归。
若当前遍历到的结点对应的数据域值小于目标值n，则应该在右子树里进一步查找，设置下一步的遍历范围为 root.right 后，继续递归。

编码实现

js 复制代码

function search(root, n) {
    // 若 root 为空，查找失败，直接返回
    if(!root) {
        return 
    }
    // 找到目标结点，输出结点对象
    if(root.val === n) {
        console.log('目标结点是：', root)
    } else if(root.val > n) {
        // 当前结点数据域大于n，向左查找
        search(root.left, n)
    } else {
        // 当前结点数据域小于n，向右查找
        search(root.right, n)
    }
}

插入新结点

插入结点的思路其实和寻找结点非常相似。大家反思一下，在上面寻找结点的时候，为什么我们会在判定当前结点为空时，就认为查找失败了呢？

这是因为，二叉搜索树的查找路线是一个非常明确的路径：我们会根据当前结点值的大小，决定路线应该是向左走还是向右走。如果最后走到了一个空结点处，这就意味着我们没有办法再往深处去搜索了，也就没有了找到目标结点的可能性。

换一个角度想想，如果这个空结点所在的位置恰好有一个值为 n 的结点，是不是就可以查找成功了？那么如果我把 n 值塞到这个空结点所在的位置，是不是刚好符合二叉搜索树的排序规则？

实不相瞒，二叉搜索树插入结点的过程，和搜索某个结点的过程几乎是一样的：从根结点开始，把我们希望插入的数据值和每一个结点作比较。若大于当前结点，则向右子树探索；若小于当前结点，则向左子树探索。最后找到的那个空位，就是它合理的栖身之所。

编码实现

js 复制代码

function insertIntoBST(root, n) {
    // 若 root 为空，说明当前是一个可以插入的空位
    if(!root) { 
        // 用一个值为n的结点占据这个空位
        root = new TreeNode(n)
        return root
    }
    
    if(root.val > n) {
        // 当前结点数据域大于n，向左查找
        root.left = insertIntoBST(root.left, n)
    } else {
        // 当前结点数据域小于n，向右查找
        root.right = insertIntoBST(root.right, n)
    }

    // 返回插入后二叉搜索树的根结点
    return root
}

注：你可以用这道力扣真题来验证以上插入操作的正确性。

删除指定结点

想要删除某个结点，首先要找到这个结点。在定位结点后，我们需要考虑以下情况：

结点不存在，定位到了空结点。直接返回即可。
需要删除的目标结点没有左孩子也没有右孩子------它是一个叶子结点，删掉它不会对其它结点造成任何影响，直接删除即可。
需要删除的目标结点存在左子树，那么就去左子树里寻找小于目标结点值的最大结点，用这个结点覆盖掉目标结点
需要删除的目标结点存在右子树，那么就去右子树里寻找大于目标结点值的最小结点，用这个结点覆盖掉目标结点
需要删除的目标结点既有左子树、又有右子树，这时就有两种做法了：要么取左子树中值最大的结点，要么取右子树中取值最小的结点。两个结点中任取一个覆盖掉目标结点，都可以维持二叉搜索树的数据有序性

编码实现

js 复制代码

function deleteNode(root, n) {
    // 如果没找到目标结点，则直接返回
    if(!root) {
        return root
    }
    // 定位到目标结点，开始分情况处理删除动作
    if(root.val === n) {
        // 若是叶子结点，则不需要想太多，直接删除
        if(!root.left && !root.right) {
            root = null
        } else if(root.left) {
            // 寻找左子树里值最大的结点
            const maxLeft = findMax(root.left)
            // 用这个 maxLeft 覆盖掉需要删除的当前结点  
            root.val = maxLeft.val
            // 覆盖动作会消耗掉原有的 maxLeft 结点
            root.left = deleteNode(root.left, maxLeft.val)
        } else {
            // 寻找右子树里值最小的结点
            const minRight = findMin(root.right)
            // 用这个 minRight 覆盖掉需要删除的当前结点  
            root.val = minRight.val
            // 覆盖动作会消耗掉原有的 minRight 结点
            root.right = deleteNode(root.right, minRight.val)
        }
    } else if(root.val > n) {
        // 若当前结点的值比 n 大，则在左子树中继续寻找目标结点
        root.left = deleteNode(root.left, n)
    } else  {
        // 若当前结点的值比 n 小，则在右子树中继续寻找目标结点
        root.right = deleteNode(root.right, n)
    }
    return root
}

// 寻找左子树最大值
function findMax(root) {
    while(root.right) {
        root = root.right
    }
    return root 
}

// 寻找右子树的最小值
function findMin(root) {
    while(root.left) {
        root = root.left
    }
    return root
}

你可以在这道力扣真题中验证以上删除操作代码的正确性。

编码复盘

上面这段代码展示了二叉搜索树删除的基本思路：在这个思路的基础上，大家可以做很多个性化的修改。

举个例子，细心的同学会发现，如果目标结点既有左子树又有右子树，那么在上面这段逻辑里，会优先去找它左子树里的最大值，而不会去 care 右子树的最小值这个选项。

这样做，得到的结果从正确性上来说是没问题的，但是却不太美观：每次都删除一侧子树的结点，会导致二叉树的左右子树高度不平衡。

如果题目中要求我们顾及二叉树的平衡度，那么我们就可以在删除的过程中记录子树的高度，每次选择高度较高的子树作为查找目标，用这个子树里的结点去覆盖需要删除的目标结点。

（关于二叉树平衡度的知识，我们会在下一节作讲解，大家稍安勿躁）

二叉搜索树的特性

关于二叉搜索树的特性，有且仅有一条是需要大家背诵默写的：
二叉搜索树的中序遍历序列是有序的！

OK，基本功就修炼到这里，下面大家一起来开开心心地碾碎真题吧！

真题实战环节

开篇我们说过，我们只要能够把握好二叉搜索树的限制条件（即定义）和特性，就足以应对大部分的考题。下面我们就来看看定义和特性的考察是如何在真题中体现的：

对定义的考察：二叉搜索树的验证

题目描述：给定一个二叉树，判断其是否是一个有效的二叉搜索树。

假设一个二叉搜索树具有如下特征：

节点的左子树只包含小于当前节点的数。

节点的右子树只包含大于当前节点的数。

所有左子树和右子树自身必须也是二叉搜索树。
示例 1:

输入:

markdown 复制代码

    2
   / \
  1   3

输出: true
示例 2:

输入:

markdown 复制代码

输出: false

解释: 输入为: [5,1,4,null,null,3,6]。

根节点的值为 5 ，但是其右子节点值为 4 。

思路分析

对于这道题，我们需要好好咀嚼一下二叉搜索树的定义：

它可以是一棵空树
它可以是一棵由根结点、左子树、右子树组成的树，同时左子树和右子树都是二叉搜索树，且左子树 上所有结点的数据域都小于等于 根结点的数据域，右子树 上所有结点的数据域都大于等于根结点的数据域

只有符合以上两种情况之一的二叉树，可以称之为二叉搜索树。

空树的判定比较简单，关键在于非空树的判定：需要递归地对非空树中的左右子树进行遍历，检验每棵子树中是否都满足 左 < 根 < 右 这样的关系（注意题中声明了不需要考虑相等情况）。

基于这样的思路，我们可以编码如下：

编码实现

js 复制代码

/**
 * @param {TreeNode} root
 * @return {boolean}
 */
const isValidBST = function(root) {
  // 定义递归函数
  function dfs(root, minValue, maxValue) {
      // 若是空树，则合法
      if(!root) {
          return true
      }
      // 若右孩子不大于根结点值，或者左孩子不小于根结点值，则不合法
      if(root.val <= minValue || root.val >= maxValue) return false
      // 左右子树必须都符合二叉搜索树的数据域大小关系
      return dfs(root.left, minValue,root.val) && dfs(root.right, root.val, maxValue)
  }
  // 初始化最小值和最大值为极小或极大
  return dfs(root, -Infinity, Infinity)
};

编码复盘

这个题的编码实现比较有意思，对 minValue 和 maxValue 的处理值得我们反刍一下：

递归过程中，起到决定性作用的是这两个判定条件：

左孩子的值是否小于根结点值
右孩子的值是否大于根结点值

在递归式中，如果单独维护一段逻辑，用于判定当前是左孩子还是右孩子，进而决定是进行大于判定还是小于判定，也是没问题的。但是在上面的编码中我们采取了一种更简洁的手法，通过设置 minValue 和 maxValue 为极小和极大值，来确保 root.val <= minValue || root.val >= maxValue 这两个条件中有一个是一定为 false 的。

比如当前我需要检查的是root 的左孩子，那么就会进入 dfs(root.left, minValue,root.val) 这段逻辑。这个dfs调用将最大值更新为了root根结点的值，将当前root结点更新为了左孩子结点，同时保持最小值为 -Infinity 不变。进入 dfs逻辑后，root.val <= minValue || root.val >= maxValue 中的 root.val <= minValue 一定为 false ，起决定性作用的条件实际是 root.val >= maxValue（这里这个 maxValue 正是根结点的数据域值)。若root.val >= maxValue返回 true，就意味着左孩子的值大于等于（也就是不小于）根结点的数据域值，这显然是不合法的。此时整个或语句都会返回true，递归式返回false，二叉搜索树进而会被判定为不合法。

对特性的考察：将排序数组转化为二叉搜索树

题目描述：将一个按照升序排列的有序数组，转换为一棵高度平衡二叉搜索树。

本题中，一个高度平衡二叉树是指一个二叉树每个节点的左右两个子树的高度差的绝对值不超过 1。
示例: 给定有序数组: [-10,-3,0,5,9],

一个可能的答案是：[0,-3,9,-10,null,5]，它可以表示下面这个高度平衡二叉搜索树：

markdown 复制代码

思路分析

这道题出现在这个位置真是太棒了（陶醉脸），它不仅是一道典型的二叉搜索树应用题，还涉及到了平衡二叉树的基本知识，对下一个专题的学习起到了很好的铺垫作用。

做这个题，大家可以先观察一下它的输入和输出，你会发现它们之间有着很微妙的关系。先看输入：

js 复制代码

[-10,-3,0,5,9]

再看输出：

js 复制代码

这个二叉树从形状上来看，像不像是把数组从 0 这个中间位置给"提起来"了？

别笑，我们接下来要做的事情，还真就是要想办法把这个数组给"提"成二叉树。

在想办法之前，我们先来反思一下为什么可以通过"提起来"来实现数组到目标二叉树的转换，这里面蕴含了两个依据：

二叉搜索树的特性：题目中指明了目标树是一棵二叉搜索树，二叉搜索树的中序遍历序列是有序的，题中所给的数组也是有序的，因此我们可以认为题目中给出的数组就是目标二叉树的中序遍历序列 。中序遍历序列的顺序规则是 左 -> 根 -> 右，因此数组中间位置的元素一定对应着目标二叉树的根结点。以根结点为抓手，把这个数组"拎"起来，得到的二叉树一定是符合二叉搜索树的排序规则的。
平衡二叉树的特性：虽然咱们还没有讲啥是平衡二叉树，但是题目中已经妥妥地给出了一个平衡二叉树的定义：

一个高度平衡二叉树是指一个二叉树每个节点的左右两个子树的高度差的绝对值不超过 1。

要做到这一点，只需要把"提起来"这个动作贯彻到底就行了：当我们以有序数组的中间元素为根结点，"提"出一个二叉树时，有两种可能的情况：

数组中元素为奇数个，此时以数组的中间元素为界，两侧元素个数相同：

js 复制代码

[-10,-3,0,5,9]

如果我们以中间元素为根结点，把数组"提"成二叉树，那么根结点左右两侧的元素个数是一样的，所以站在根结点来看，左右子树的高度差为0：

js 复制代码

数组中元素为偶数个，此时无论是选择中间靠左的元素为界、还是选择中间靠右的元素为界，两侧元素个数差值的绝对值都是1：

js 复制代码

[-10,-3,0,5]

在这个例子里，若以 -3 为根结点，那么左右子树的高度差的绝对值就是1：

js 复制代码

以 0 为根结点亦然。

通过对以上情况进行探讨，我们发现"以中间元素为根结点，将数组提成树"这种操作，可以保证根结点左右两侧的子树高度绝对值不大于1。要想保证每一棵子树都满足这个条件，我们只需要对有序数组的每一个对半分出来的子序列都递归地执行这个操作即可。

编码实现

js 复制代码

/**
 * @param {number[]} nums
 * @return {TreeNode}
 */
const sortedArrayToBST = function(nums) {
    // 处理边界条件
    if(!nums.length) {
        return null
    }
    
    // root 结点是递归"提"起数组的结果
    const root = buildBST(0, nums.length-1)

    // 定义二叉树构建函数，入参是子序列的索引范围
    function buildBST(low, high) {
        // 当 low > high 时，意味着当前范围的数字已经被递归处理完全了
        if(low > high) {
            return null
        }
        // 二分一下，取出当前子序列的中间元素
        const mid = Math.floor(low + (high - low)/2)  
        // 将中间元素的值作为当前子树的根结点值
        const cur = new TreeNode(nums[mid]) 
        // 递归构建左子树，范围二分为[low,mid)
        cur.left = buildBST(low,mid-1)
        // 递归构建左子树，范围二分为为(mid,high]
        cur.right = buildBST(mid+1, high)
        // 返回当前结点
        return cur
    }
    // 返回根结点
    return root
};

（阅读过程中有任何想法或疑问，或者单纯希望和笔者交个朋友啥的，欢迎大家添加我的微信xyalinode与我交流哈~）二叉搜索树是二叉树的特例，平衡二叉树则是二叉搜索树的特例。

什么是平衡二叉树

在上一节的末尾，我们已经通过一道真题和平衡二叉树打过交道。正如题目中所说，平衡二叉树（又称 AVL Tree）指的是任意结点 的左右子树高度差绝对值都不大于1 的二叉搜索树。

为什么要有平衡二叉树

平衡二叉树的出现，是为了降低二叉搜索树的查找时间复杂度。

大家知道，对于同样一个遍历序列，二叉搜索树的造型可以有很多种。拿 [1,2,3,4,5]这个中序遍历序列来说，基于它可以构造出的二叉搜索树就包括以下两种造型：

结合平衡二叉树的定义，我们可以看出，第一棵二叉树是平衡二叉树，第二棵二叉树是普通的二叉搜索树。

现在，如果要你基于上一节学过的二叉搜索树查找算法，在图上两棵树上分别找出值为1的结点，问你各需要查找几次？在1号二叉树中，包括根结点在内，只需要查找3次；而在2号二叉树中，包括根结点在内，一共需要查找5次。

我们发现，在这个例子里，对于同一个遍历序列来说，平衡二叉树比非平衡二叉树（图上的结构可以称为链式二叉树）的查找效率更高。这是为什么呢？

大家可以仔细想想，为什么科学家们会无中生有，给二叉树的左右子树和根结点之间强加上排序关系作为约束，进而创造出二叉搜索树这种东西呢？难道只是为了装x吗？当然不是啦。二叉搜索树的妙处就在于它把"二分"这种思想以数据结构的形式表达了出来 。在一个构造合理的二叉搜索树里，我们可以通过对比当前结点和目标值之间的大小关系，缩小下一步的搜索范围（比如只搜索左子树或者只搜索右子树），进而规避掉不必要的查找步骤，降低搜索过程的时间复杂度。但是如果一个二叉搜索树严重不平衡，比如说上面这棵链式搜索树：

每一个结点的右子树都是空的，这样的结构非常不合理，它会带来高达O(N)的时间复杂度。而平衡二叉树由于利用了二分思想，查找操作的时间复杂度仅为 O(logN)。因此，为了保证二叉搜索树能够确实为查找操作带来效率上的提升，我们有必要在构造二叉搜索树的过程中维持其平衡度，这就是平衡二叉树的来由。

命题思路解读

平衡二叉树和二叉搜索树一样，都被归类为"特殊"的二叉树。对于这样的数据结构来说，其"特殊"之处也正是其考点所在，因此真题往往稳定地分布在以下两个方向：

对特性的考察（本节以平衡二叉树的判定为例）
对操作的考察（本节以平衡二叉树的构造为例）

平衡二叉树的判定

题目描述：给定一个二叉树，判断它是否是高度平衡的二叉树。

本题中，一棵高度平衡二叉树定义为：一个二叉树每个节点的左右两个子树的高度差的绝对值不超过1。
示例 1: 给定二叉树 [3,9,20,null,null,15,7]

markdown 复制代码

返回 true 。
示例 2: 给定二叉树 [1,2,2,3,3,null,null,4,4]

markdown 复制代码

返回 false 。

思路分析

来，我们复习一遍平衡二叉树的定义：

平衡二叉树是任意结点 的左右子树高度差绝对值都不大于1 的二叉搜索树。抓住其中的三个关键字：

任意结点
左右子树高度差绝对值都不大于1
二叉搜索树

注意，结合题意，上面3个关键字中的3对这道题来说是不适用的，因此我们不必对二叉搜索树的性质进行校验。现在只看 1 和 2，先给自己一分钟思考一下------你可以提取出什么线索？

"任意结点"什么意思？每一个结点都需要符合某个条件，也就是说每一个结点在被遍历到的时候都需要重复某个校验流程，对不对？

哎，我刚刚是不是说了什么不得了的动词了？啊，是重复！是tmd的重复啊！！！来，学到了第18节，为了向我证明你没有跳读，请大声喊出下面这两个字：

递归！
没错，"任意结点"这四个字，就是在暗示你用递归。而"左右子树高度差绝对值都不大于1"这个校验规则，就是递归式。

啊，真让人激动呢，解决这道题的思路竟然已经慢慢浮现出来了，那就是：从下往上递归遍历树中的每一个结点，计算其左右子树的高度并进行对比，只要有一个高度差的绝对值大于1，那么整棵树都会被判为不平衡。

编码实现

js 复制代码

const isBalanced = function(root) {
  // 立一个flag，只要有一个高度差绝对值大于1，这个flag就会被置为false
  let flag = true
  // 定义递归逻辑
  function dfs(root) {
      // 如果是空树，高度记为0；如果flag已经false了，那么就没必要往下走了，直接return
      if(!root || !flag) {
          return 0 
      }
      // 计算左子树的高度
      const left = dfs(root.left)  
      // 计算右子树的高度
      const right = dfs(root.right)  
      // 如果左右子树的高度差绝对值大于1，flag就破功了
      if(Math.abs(left-right) > 1) {
          flag = false
          // 后面再发生什么已经不重要了，返回一个不影响回溯计算的值
          return 0
      }
      // 返回当前子树的高度
      return Math.max(left, right) + 1
  }
  
  // 递归入口
  dfs(root) 
  // 返回flag的值
  return flag
};

平衡二叉树的构造

题目描述：给你一棵二叉搜索树，请你返回一棵平衡后的二叉搜索树，新生成的树应该与原来的树有着相同的节点值。

如果一棵二叉搜索树中，每个节点的两棵子树高度差不超过 1 ，我们就称这棵二叉搜索树是平衡的。

如果有多种构造方法，请你返回任意一种。
示例：

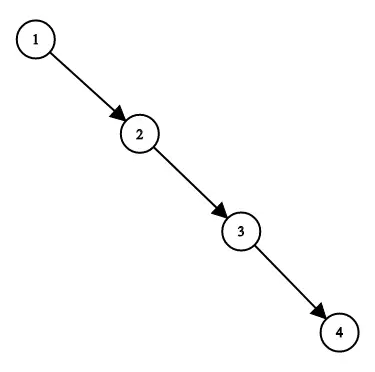
输入：root = [1,null,2,null,3,null,4,null,null]

输出：[2,1,3,null,null,null,4]

解释：这不是唯一的正确答案，[3,1,4,null,2,null,null] 也是一个可行的构造方案。
提示：

树节点的数目在 1 到 10^4 之间。树节点的值互不相同，且在 1 到 10^5 之间。

思路分析

这道题乍一看有点唬人，可能会直接干懵一部分同学。不过不用慌------题目再新，套路依旧。只要你对核心考点把握得足够扎实，它就难不倒你。

我们来分析一下这道题的核心诉求：要求我们构造一棵平衡的二叉搜索树。先抛开题干中各种前置条件不谈，单看这个输出结果，你会不会有一种似曾相识的感觉呢？没错，在上一节的最后一道真题中，我们也构造过这样的一棵二叉树。

那么这两道题之间会不会有什么微妙的联系呢？答案是会，不然，笔者也不会把它们放得这么近（疯狂暗示）。两道题之间唯一的差别在于输入：在我们已经做过的那道题中，输入参数是一个有序数组；而这道题中，输入参数是一个二叉搜索树。

唔，再想想！上一节那道题里的"有序数组"，和眼前这道题里的"二叉搜索树"之间，会不会有什么妙不可言的关系呢？

别忘了，二叉搜索树的中序遍历序列是有序的！所谓有序数组，完全可以理解为二叉搜索树的中序遍历序列啊，对不对？现在树都给到咱们手里了，求它的中序遍历序列是不是非常 easy？如果能把中序遍历序列求出来，这道题是不是就跟之前做过那道是一模一样的解法了？

没错，这道题的解题思路正是：

中序遍历求出有序数组
逐个将二分出来的数组子序列"提"起来变成二叉搜索树

编码实现

js 复制代码

/**
 * @param {TreeNode} root
 * @return {TreeNode}
 */
const balanceBST = function(root) {
    // 初始化中序遍历序列数组
    const nums = []
    // 定义中序遍历二叉树，得到有序数组
    function inorder(root) {
        if(!root) {
            return 
        }
        inorder(root.left)  
        nums.push(root.val)  
        inorder(root.right)
    }
    
    // 这坨代码的逻辑和上一节最后一题的代码一模一样
    function buildAVL(low, high) {
        // 若 low > high，则越界，说明当前索引范围对应的子树已经构建完毕
        if(low>high) {
            return null
        }
        // 取数组的中间值作为根结点值
        const mid = Math.floor(low + (high -low)/2)
        // 创造当前树的根结点
        const cur = new TreeNode(nums[mid])  
        // 构建左子树
        cur.left = buildAVL(low, mid-1) 
        // 构建右子树
        cur.right = buildAVL(mid+1, high)  
        // 返回当前树的根结点 
        return cur
    }
    // 调用中序遍历方法，求出 nums
    inorder(root)
    // 基于 nums，构造平衡二叉树
    return buildAVL(0, nums.length-1)
};

本节内容不要求所有同学掌握------如果你在阅读的过程中，觉得理解起来非常吃力，笔者建议你暂时跳过这一节，优先完成全盘的知识点扫盲后再回来看。

为什么这样说？这里面有两个原因：

根据笔者长期奋战算法面试一线的经验，能用堆结构解决的问题，基本上也都能用普通排序来解决。
即便是后端工程师或者算法工程师，能够在面试现场手写堆结构的人也寥寥无几。这倒不是因为他们不够专业，而是因为他们基本都非常熟悉一门叫做 JAVA 的语言------JAVA大法好，它在底层封装了一个叫做priorty_queue的数据结构，这个数据结构把堆的构建、插入、删除等操作全部做掉了。所以说这帮人非常喜欢做堆/优先队列相关的题目，调几个API就完事儿了。

那么为什么还要讲堆结构，堆结构在我们整个知识体系里的定位应该怎么去把握，这里有两件事情希望大家能明白：

几乎每一本正经的计算机专业数据结构教材，都会介绍堆结构。小册本身虽然是面向面试的，但笔者更希望能借这个机会，帮助一部分没有机会接受科班教育的前端同行补齐自身的知识短板。
笔者个人在素材调研期间经历过的 N 次涉及算法的前端面试中，有1次真的考到了需要用堆结构解决的问题（这道题在下面的讲解中也会出现）。当时笔者还不知道堆的玩法，直接用JS的排序API做出来了。事后和面试官聊天的时候，突然被他要求用堆结构再做一遍。最后虽然在没写出来的情况下拿到了offer，但事后想起来，还是非常后怕------没有人能预知自己下一次遇到的面试官到底是什么脾气，我们只能尽自己所能地去做万全的准备。

前置知识：完全二叉树

完全二叉树是指同时满足下面两个条件的二叉树：

从第一层到倒数第二层，每一层都是满的，也就是说每一层的结点数都达到了当前层所能达到的最大值
最后一层的结点是从左到右连续排列的，不存在跳跃排列的情况（也就是说这一层的所有结点都集中排列在最左边）。

完全二叉树可以是这样的：

也可以是这样的：

但不能是这样的：

更不能是这样的：

注意，完全二叉树中有着这样的索引规律：假如我们从左到右、从上到下依次对完全二叉树中的结点从0开始进行编码：

那么对于索引为 n 的结点来说：

索引为 (n-1)/2 的结点是它的父结点
索引 2*n+1 的结点是它的左孩子结点
索为引 2*n+2 的结点是它的右孩子结点

什么是堆

堆是完全二叉树的一种特例。根据约束规则的不同，堆又分为两种：

大顶堆
小顶堆

如果对一棵完全二叉树来说，它每个结点的结点值都不小于其左右孩子的结点值，这样的完全二叉树就叫做"大顶堆"：

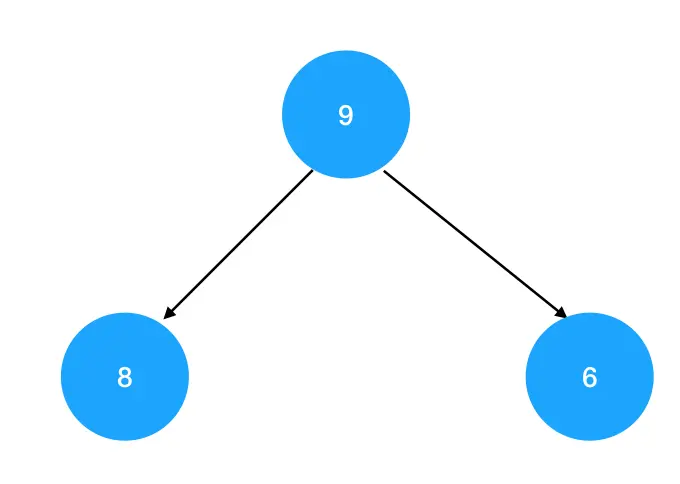若树中每个结点值都不大于其左右孩子的结点值，这样的完全二叉树就叫做"小顶堆"

堆的基本操作：以大顶堆为例

大顶堆和小顶堆除了约束条件中的大小关系规则完全相反以外，其它方面都保持高度一致。现在我们以大顶堆为例，一起来看看堆结构有哪些玩法。

这里我给出一个现成的大顶堆：

很多时候，为了考察你对完全二叉树索引规律的掌握情况，题目中与堆结构同时出现的，还有它的层序遍历序列：

js 复制代码

[9, 8, 6, 3, 1]

（现在赶快回去复习一下完全二叉树的索引规律，我们马上写代码要用到了）

我们需要关注的动作有两个：

如何取出堆顶元素（删除操作）
往堆里追加一个元素（插入操作）

至于堆的初始化，也只不过是从空堆开始，重复执行动作2而已。因此，上面这两个动作就是堆操作的核心。

取出堆顶元素

取出元素本身并不难，难的是如何在删除元素的同时，保持住队的"大顶"结构特性。为了做到这点，我们需要执行以下操作：

用堆里的最后一个元素（对应图中的数字1）替换掉堆顶元素。
对比新的堆顶元素（1）与其左右孩子的值，如果其中一个孩子大于堆顶元素，则交换两者的位置：

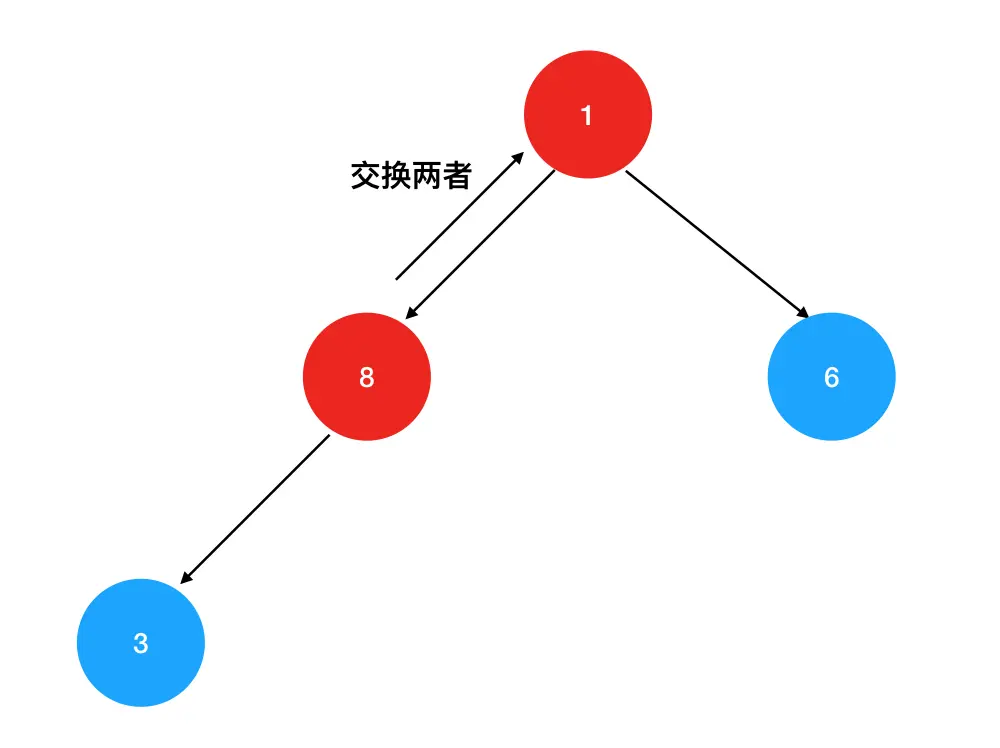交换后，继续向下对比1与当前左右孩子的值，如果其中一个大于1，则交换两者的位置：

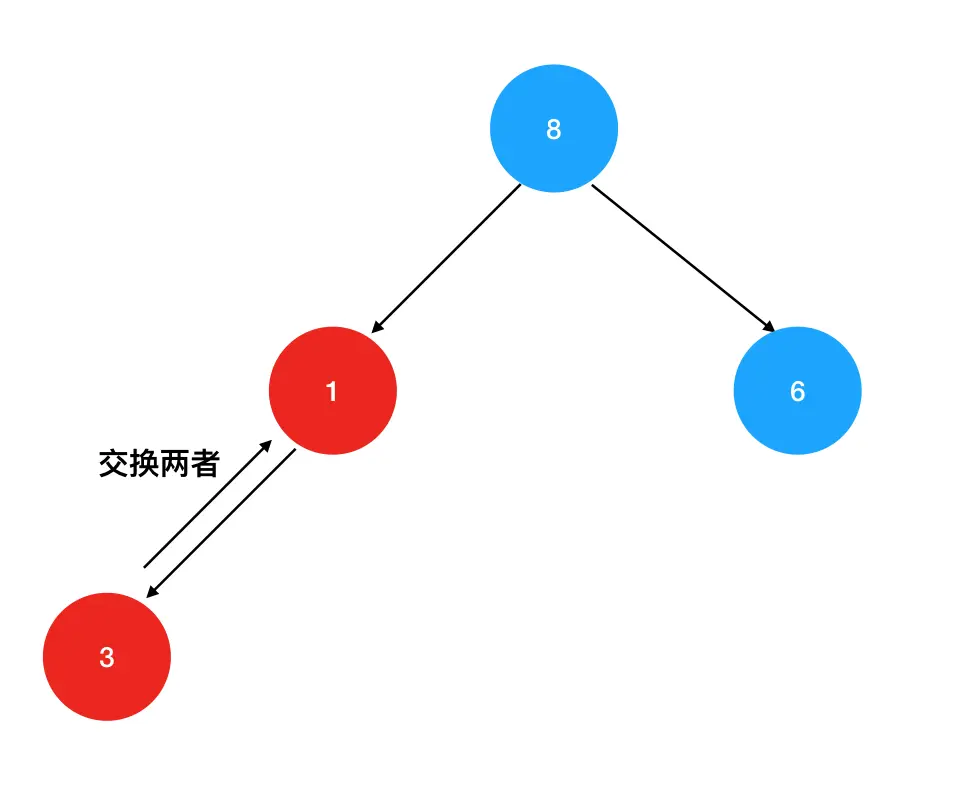重复这个向下对比+交换的过程，直到无法继续交换为止，我们就得到了一个符合"大顶"原则的新的堆结构：

上述这个反复向下对比+交换的过程，用编码实现如下（仔细看注释）：

js 复制代码

// 入参是堆元素在数组里的索引范围，low表示下界，high表示上界
function downHeap(low, high) {
    // 初始化 i 为当前结点，j 为当前结点的左孩子
    let i=low,j=i*2+1 
    // 当 j 不超过上界时，重复向下对比+交换的操作
    while(j <= high) {
        // 如果右孩子比左孩子更大，则用右孩子和根结点比较
        if(j+1 <= high && heap[j+1] > heap[j]) {
            j = j+1
        }
        
        // 若当前结点比孩子结点小，则交换两者的位置，把较大的结点"拱上去"
        if(heap[i] < heap[j]) {
            // 交换位置
            const temp = heap[j]  
            heap[j] = heap[i]  
            heap[i] = temp
            
            // i 更新为被交换的孩子结点的索引
            i=j  
            // j 更新为孩子结点的左孩子的索引
            j=j*2+1
        } else {
            break
        }
    }
}

往堆里追加一个元素

当添加一个新元素进堆的时候，我们同样需要考虑堆结构的排序原则：

新来的数据首先要追加到当前堆里最后一个元素的后面。比如我现在要新增一个10，它就应该排在最后一层的最后一个位置：

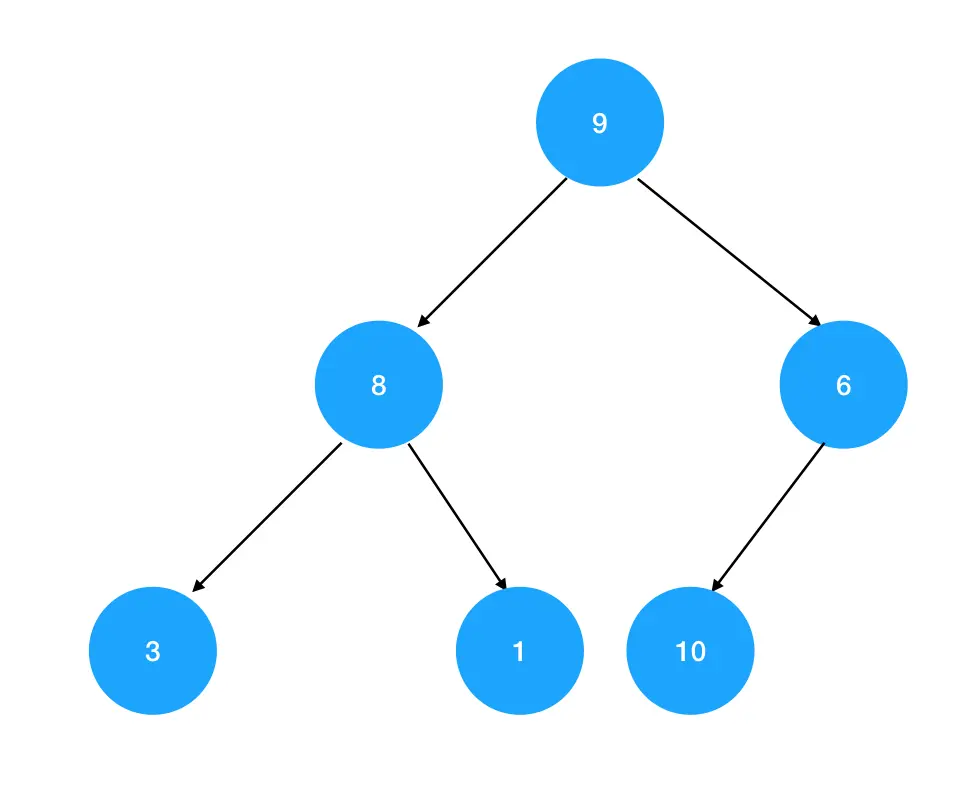2. 不断进行向上对比+交换的操作：如果发现10比父结点的结点值要大，那么就和父结点的元素相互交换，再接着往上进行比较，直到无法再继续交换为止。首先被比下去的是值为6的直接父结点：

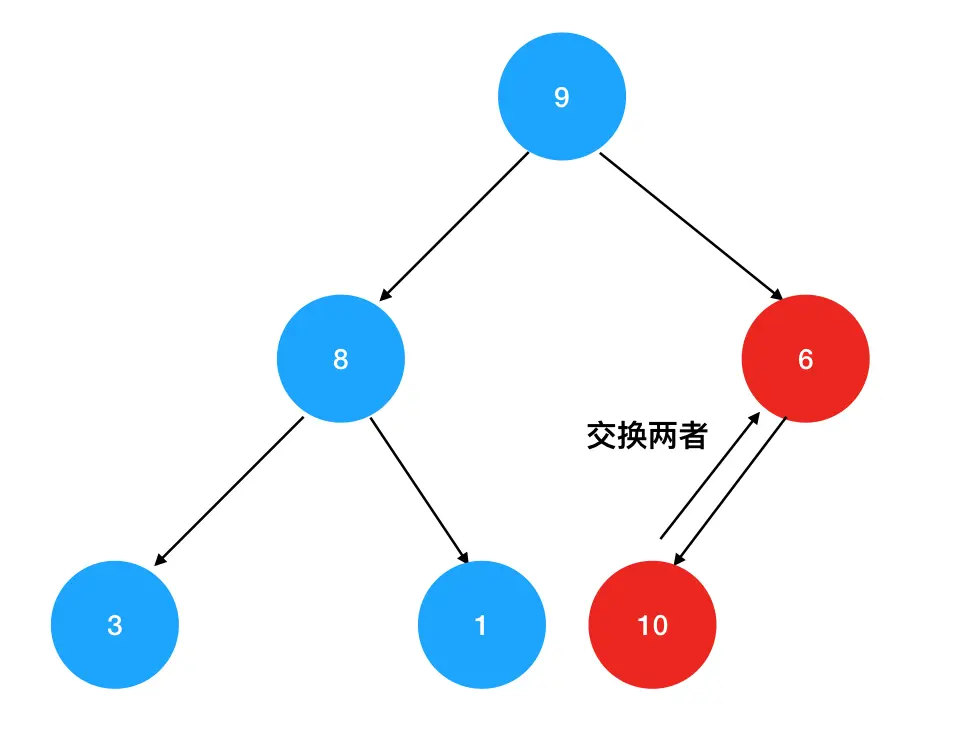接着继续往上找，发现10比根结点9还要大，于是继续进行交换：

根结点被换掉后，再也无法向上比较了。此时，我们已经得到了一个追加过数字10的新的堆结构：

上述这个反复向上对比+交换的过程，用编码实现如下（仔细看注释）：

js 复制代码

// 入参是堆元素在数组里的索引范围，low表示下界，high表示上界
function upHeap(low, high) {
    // 初始化 i（当前结点索引）为上界
    let i = high  
    // 初始化 j 为 i 的父结点
    let j = Math.floor((i-1)/2)  
    // 当 j 不逾越下界时，重复向上对比+交换的过程
    while(j>=low)  {
        // 若当前结点比父结点大
        if(heap[j]<heap[i]) {
            // 交换当前结点与父结点，保持父结点是较大的一个
            const temp = heap[j] 
            heap[j] = heap[i]  
            heap[i] = temp
            
            // i更新为被交换父结点的位置
            i=j   
            // j更新为父结点的父结点
            j=Math.floor((i-1)/2)  
        } else {
            break
        }
    }
}

上面这两个过程，需要大家反复理解、深刻记忆。尤其是要记住这几个关键字："删除 "就是"向下比较+交换 "，而"添加 "则是"向上比较+交换"。

! 复制代码

这里写给大家的两段代码，在实战中具备一定的通用性。希望大家能够充分熟悉，在理解的基础上记忆。下次如果真的用到，争取能够默写。

堆结构在排序中的应用------优先队列

在认识优先队列之前，我们先来看一道题：

题目描述：在未排序的数组中找到第 k 个最大的元素。请注意，你需要找的是数组排序后的第 k 个最大的元素，而不是第 k 个不同的元素。
示例 1:

输入: [3,2,1,5,6,4] 和 k = 2

输出: 5
示例 2: 输入: [3,2,3,1,2,4,5,5,6] 和 k = 4

输出: 4
说明:

你可以假设 k 总是有效的，且 1 ≤ k ≤ 数组的长度。

思路分析

这道题的诉求非常直接------要求你对给定数组进行排序。关于排序，我们在下一节会展开讲解N种排序算法的实现方式，包括快速排序、归并排序、选择排序等等。这些排序有一个共同的特点------在排序的过程中，你很难去明确元素之间的大小关系，只有在排序彻底完成后，你才能找出第 k 大的元素是哪个。

对整个数组进行排序、然后按顺序返回索引为k-1的元素，这正是笔者在面试场上写出的第一个解法：

js 复制代码

/**
* @param {number[]} nums
* @param {number} k
* @return {number}
*/
const findKthLargest = function(nums, k) {
 // 将数组逆序
 const sorted = nums.sort((a,b)=> {
     return b-a
 })
 // 取第k大的元素
 return sorted[k-1]
};;

是的，你没有看错，我甚至没有手动实现任何一个排序算法，而是直接调了 JS 的sort 方法。

大家不要笑，这个sort方法真的可以救命。如果你理解不了本节接下来要讲的基于堆结构的解法，又没信心记住后面两节涉及的各种各样的花式排序算法。那么你一定要紧紧抓住这个sort API。面试的时候，万一被问到"你为什么不会写xx排序算法"，这时候用一句"我用sort方法比较多，不喜欢自己造轮子"糊弄过去，还是有一定成功率的。

好了，学渣小剧场结束。我们继续来看这个题：有没有一种排序方法能够在不对所有元素进行排序的情况下，帮我们提前定位到第 k 大的元素是哪个呢？当然有------构建一个堆结构就能解决问题！

对于这道题来说，要想求出第 k 大的元素，我们可以维护一个大小为 k 的小顶堆。这个堆的初始化过程可以通过遍历并插入数组的前 k 个元素来实现。当堆被填满后，再尝试用数组的第 k+1 到末尾的这部分元素来更新这个小顶堆，更新过程中遵循以下原则：

若遍历到的数字比小顶堆的堆顶元素值大，则用该数字替换掉小顶堆的堆顶元素值
若遍历到的数字比小顶堆的堆顶元素值小，则忽略这个数字

仔细想想，为什么要这样做？假设数组中元素的总个数是 n，那么：

维护大小为 k 的小顶堆的目的，是为了确保堆中除了堆顶元素之外的 k-1 个元素值都大于堆顶元素。
当我们用数组的[0, k-1]区间里的数字初始化完成这个堆时，堆顶元素值就对应着前 k 个数字里的最小值。
紧接着我们尝试用索引区间为 [k, n-1]的数字来更新堆，在这个过程中，只允许比堆顶元素大的值进入堆 。这一波操作过后，堆里的 k 个数字就是整个数组中最大的 k 个数字，而堆顶的数字正是这 k 个数中最小的那个。于是本题得解。

我们用示例中的[3,2,1,5,6,4]这个序列来模拟一下上面的过程。初始化一个规模为 k=2 的小顶堆，它长这样：

markdown 复制代码

    2
   /
  3

用[k, n-1]索引范围内的元素来更新这个小顶堆：首先是用索引为2的数字1来试，发现1比堆顶的2还要小，忽略它。接着用索引为3的5来试，5是比2大的，用它把2换掉：

markdown 复制代码

    5
   /
  3

经过向下对比+调整，新的堆长这样：

markdown 复制代码

    3
   /
  5

我们发现，现在这个堆里面保存的正是索引范围[0, 3]内的前 k 个最大的数。以此类推，当对数组中最后一个元素执行过尝试入堆的逻辑后，堆里面保存的就是整个数组范围内的前 k 个最大的数。

在解题的过程中，不出所料地用到了上文中提及的downHeap方法和upHeap 方法。不过大家千万不要直接复制粘贴，别忘了，前面我们是用大顶堆举例，这道题需要构造的是小顶堆------记得调整大小关系规则。

（一切尽在注释中，不要只记得抄代码啊年轻人）

js 复制代码

/**
* @param {number[]} nums
* @param {number} k
* @return {number}
*/
const findKthLargest = function(nums, k) {
   // 初始化一个堆数组
   const heap = []  
   // n表示堆数组里当前最后一个元素的索引
   let n = 0
   // 缓存 nums 的长度
   const len = nums.length  
   // 初始化大小为 k 的堆
   function createHeap() {
       for(let i=0;i<k;i++) {
           // 逐个往堆里插入数组中的数字
           insert(nums[i])
       }
   }
   
   // 尝试用 [k, n-1] 区间的元素更新堆
   function updateHeap() {
       for(let i=k;i<len;i++) {
           // 只有比堆顶元素大的才有资格进堆
           if(nums[i]>heap[0]) {
               // 用较大数字替换堆顶数字
               heap[0] = nums[i]  
               // 重复向下对比+交换的逻辑
               downHeap(0, k)
           }
       }
   }
   
   // 向下对比函数
   function downHeap(low, high) {
       // 入参是堆元素在数组里的索引范围，low表示下界，high表示上界
       let i=low,j=i*2+1 
       // 当 j 不超过上界时，重复向下对比+交换的操作
       while(j<=high) {
           // // 如果右孩子比左孩子更小，则用右孩子和根结点比较
           if(j+1<=high && heap[j+1]<heap[j]) {
               j = j+1
           }
           
           // 若当前结点比孩子结点大，则交换两者的位置，把较小的结点"拱上去"
           if(heap[i] > heap[j]) {
               // 交换位置
               const temp = heap[j]  
               heap[j] = heap[i]  
               heap[i] = temp
               
               // i 更新为被交换的孩子结点的索引
               i=j  
               // j 更新为孩子结点的左孩子的索引
               j=j*2+1
           } else {
               break
           }
       }
   }
   
   // 入参是堆元素在数组里的索引范围，low表示下界，high表示上界
   function upHeap(low, high) {
       // 初始化 i（当前结点索引）为上界
       let i = high  
       // 初始化 j 为 i 的父结点
       let j = Math.floor((i-1)/2)  
       // 当 j 不逾越下界时，重复向上对比+交换的过程
       while(j>=low)  {
           // 若当前结点比父结点小
           if(heap[j]>heap[i]) {
               // 交换当前结点与父结点，保持父结点是较小的一个
               const temp = heap[j] 
               heap[j] = heap[i]  
               heap[i] = temp
               
               // i更新为被交换父结点的位置
               i=j   
               // j更新为父结点的父结点
               j=Math.floor((i-1)/2)  
           } else {
               break
           }
       }
   }

   // 插入操作=将元素添加到堆尾部+向上调整元素的位置
   function insert(x) {
       heap[n] = x  
       upHeap(0, n)
       n++
   }
   
   // 调用createHeap初始化元素个数为k的队
   createHeap()
   // 调用updateHeap更新堆的内容，确保最后堆里保留的是最大的k个元素
   updateHeap()
   // 最后堆顶留下的就是最大的k个元素中最小的那个，也就是第k大的元素
   return heap[0]
};

编码复盘

上面这个题解中出现的 heap 数组，就是一个优先队列。

优先队列的本质是二叉堆结构，它具有以下特性：

队列的头部元素，也即索引为0的元素，就是整个数组里的最值------最大值或者最小值
对于索引为 i 的元素来说，它的父结点下标是 (i-1)/2（上面咱们讲过了，这与完全二叉树的结构特性有关）
对于索引为 i 的元素来说，它的左孩子下标应为2*i+1，右孩子下标应为2*i+2。

当题目中出现类似于"第k大"或者"第k高"这样的关键字时，就是在暗示你用优先队列/堆结构来做题------这样的手法可以允许我们在不对序列进行完全排序的情况下，找到第 k 个最值。

在其它语言的算法面试中，优先队列可以直接借助语言本身提供的数据结构来实现（比如JAVA中的priority_queue）。但在 JS 中，我们只能手动造轮子。因此，优先队列在前端算法面试中的权重并不高。如果本节内容让你感觉学起来有难度，那么也不用灰心，更不必焦虑------把握好下一节开始的排序算法专题，上了考场你仍然是一条好汉。

链表结构相对数组、字符串来说，稍微有那么一些些复杂，所以针对链表的真题戏份也相对比较多。

前面咱们说过，数组、字符串若想往难了出，那一定是要结合一些超越数据结构本身的东西------比如排序算法、二分思想、动态规划思想等等。因此，这部分对应的难题、综合题，我们需要等知识体系完全构建起来之后，在真题训练环节重新复盘。

但是链表可不一样了。如果说在命题时，数组和字符串的角色往往是"算法思想的载体"，那么链表本身就可以被认为是"命题的目的"。单在真题归纳解读环节，我们能讲的技巧、能做的题目已经有很多。结合实际面试中的命题规律，我把这些题目分为以下三类：

链表的处理：合并、删除等（删除操作画个记号，重点中的重点！）
链表的反转及其衍生题目
链表成环问题及其衍生题目

本节我们就以链表的处理为切入点，一步一步走进链表的世界。

链表的合并

真题描述：将两个有序链表合并为一个新的有序链表并返回。新链表是通过拼接给定的两个链表的所有结点组成的。
示例：输入：1->2->4, 1->3->4 输出：1->1->2->3->4->4

思路分析

做链表处理类问题，大家要把握住一个中心思想------处理链表的本质，是处理链表结点之间的指针关系 。

这道题也不例外，我们先来看看处理前两个链表的情况：

两个链表如果想要合并为一个链表，我们恰当地补齐双方之间结点 next 指针的指向关系，就能达到目的。

如果这么说仍然让你觉得抽象，那么大家不妨把图上的6个结点想象成6个扣子：现在的情况是，6个扣子被分成了两拨，各自由一根线把它们穿起来。而我们的目的是让这六个扣子按照一定的顺序，串到一根线上去。这时候需要咱们做的就是一个穿针引线的活儿，现在线有了，咱缺的是一根针：

这根针每次钻进扣子眼儿之前，要先比较一下它眼前的两个扣子，选择其中值较小的那个，优先把它串进去。一次串一个，直到所有的扣子都被串进一条线为止（下图中红色箭头表明穿针的过程与方向）：

同时我们还要考虑 l1 和 l2 两个链表长度不等的情况：若其中一个链表已经完全被串进新链表里了，而另一个链表还有剩余结点，考虑到该链表本身就是有序的，我们可以直接把它整个拼到目标链表的尾部。

编码实现

js 复制代码

/**
 * @param {ListNode} l1
 * @param {ListNode} l2
 * @return {ListNode}
 */
const mergeTwoLists = function(l1, l2) {
  // 定义头结点，确保链表可以被访问到
  let head = new ListNode()
  // cur 这里就是咱们那根"针"
  let cur = head
  // "针"开始在 l1 和 l2 间穿梭了
  while(l1 && l2) {
      // 如果 l1 的结点值较小
      if(l1.val<=l2.val) {
          // 先串起 l1 的结点
          cur.next = l1
          // l1 指针向前一步
          l1 = l1.next
      } else {
          // l2 较小时，串起 l2 结点
          cur.next = l2
          // l2 向前一步
          l2 = l2.next
      }
      
      // "针"在串起一个结点后，也会往前一步
      cur = cur.next 

  }
  
  // 处理链表不等长的情况
  cur.next = l1!==null?l1:l2
  // 返回起始结点
  return head.next
};

链表结点的删除

我们先来看一道基础题目：

真题描述：给定一个排序链表，删除所有重复的元素，使得每个元素只出现一次。
示例 1:

输入: 1->1->2

输出: 1->2

示例 2:

输入: 1->1->2->3->3

输出: 1->2->3

思路分析

链表的删除是一个基础且关键的操作，我们在数据结构部分就已经对该操作的编码实现进行过介绍，这里直接复用大家已经学过的删除能力，将需要删除的目标结点的前驱结点 next 指针往后指一格：

判断两个元素是否重复，由于此处是已排序的链表，我们直接判断前后两个元素值是否相等即可。

编码实现

js 复制代码

/**
 * @param {ListNode} head
 * @return {ListNode}
 */
const deleteDuplicates = function(head) {
    // 设定 cur 指针，初始位置为链表第一个结点
    let cur = head;
    // 遍历链表
    while(cur != null && cur.next != null) {
        // 若当前结点和它后面一个结点值相等（重复）
        if(cur.val === cur.next.val) {
            // 删除靠后的那个结点（去重）
            cur.next = cur.next.next;
        } else {
            // 若不重复，继续遍历
            cur = cur.next;
        }
    }
    return head;
};

大家不要小看了这么一道简简单单的基础题目，在实际面试中，下不了笔的、写不囫囵的、写了跑不起来的，大有人在。

一道题之所以能够成为面试题，一定有其考察意义在。拿这道题来说，既能考察你链表的遍历（while循环），又能考察你链表的 CRUD 中最热门的删除操作，候选人做这道题的情况，一定程度上可以反馈其基本功的扎实度。做对了是正常，如果做不对，那么在算法和数据结构这个考察环节，你的处境就有点危险了。

删除问题的延伸------dummy 结点登场

真题描述：给定一个排序链表，删除所有含有重复数字的结点，只保留原始链表中没有重复出现的数字。
示例 1:

输入: 1->2->3->3->4->4->5

输出: 1->2->5

示例 2:

输入: 1->1->1->2->3

输出: 2->3

思路分析

我们先来分析一下这道题和上道题有什么异同哈：相同的地方比较明显，都是删除重复元素。不同的地方在于，楼上我们删到没有重复元素就行了，可以留个"独苗"；但现在，题干要求我们只要一个元素发生了重复，就要把它彻底从链表中干掉，一个不留。

这带来了一个什么问题呢？我们回顾一下前面咱们是怎么做删除的：在遍历的过程中判断当前结点和后继结点之间是否存在值相等的情况，若有，直接对后继结点进行删除：

这个过程非常自然，为啥？因为咱们要删除某一个目标结点时，必须知道它的前驱结点。在上图中，我们本来就是站在前驱结点的位置，对其后继结点进行删除，只需要将前驱结点的 next 指针往后挪一位就行了。

但是现在，咱们要做的事情变成了把前驱和后继一起删掉，前面两个值为1的结点要一起狗带才行，起始结点直接变成了第三个：

如果继续沿用刚才的思路，我们会发现完全走不通。因为我们的 cur 指针就是从图中第一个结点出发开始遍历的，无法定位到第一个结点的前驱结点，删除便无法完成。

其实在链表题中，经常会遇到这样的问题：链表的第一个结点，因为没有前驱结点，导致我们面对它无从下手。这时我们就可以用一个 dummy 结点来解决这个问题。

所谓 dummy 结点，就是咱们人为制造出来的第一个结点的前驱结点，这样链表中所有的结点都能确保有一个前驱结点，也就都能够用同样的逻辑来处理了。

dummy 结点能够帮助我们降低链表处理过程的复杂度，处理链表时，不设 dummy 结点思路可能会打不开；设了 dummy 结点的话，就算不一定用得上，也不会出错。所以笔者个人非常喜欢用 dummy 结点。有心的同学可能也会注意到，在本节的第一题"链表的合并"中，其实也有 dummy 结点的身影。

回到这道题上来，我们首先要做的就是定义一个 dummy 结点，指向链表的起始位置：

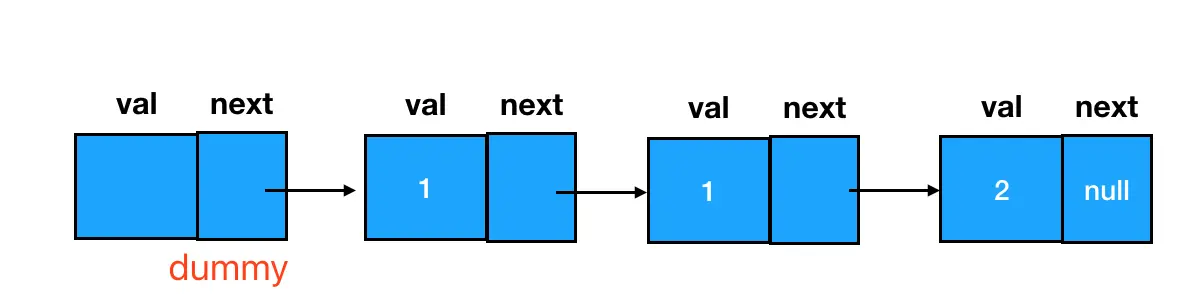这样一来，如果想要删除两个连续重复的值为 1 的结点，我们只需要把 dummy 结点的 next 指针直接指向 2：

如此一来，就大功告成啦~

注意：由于重复的结点可能不止一个两个，我们这里需要用一个 while 循环来反复地进行重复结点的判断和删除操作。

编码实现

js 复制代码

/**
 * @param {ListNode} head
 * @return {ListNode}
 */
const deleteDuplicates = function(head) {
    // 极端情况：0个或1个结点，则不会重复，直接返回
    if(!head || !head.next) {
        return head
    }
    // dummy 登场
    let dummy = new ListNode() 
    // dummy 永远指向头结点
    dummy.next = head   
    // cur 从 dummy 开始遍历
    let cur = dummy 
    // 当 cur 的后面有至少两个结点时
    while(cur.next && cur.next.next) {
        // 对 cur 后面的两个结点进行比较
        if(cur.next.val === cur.next.next.val) {
            // 若值重复，则记下这个值
            let val = cur.next.val
            // 反复地排查后面的元素是否存在多次重复该值的情况
            while(cur.next && cur.next.val===val) {
                // 若有，则删除
                cur.next = cur.next.next 
            }
        } else {
            // 若不重复，则正常遍历
            cur = cur.next
        }
    }
    // 返回链表的起始结点
    return dummy.next;
};

小结

在本节，我们对链表真题大军中的"小可爱"流派进行了剖析。通过对"小可爱"流派的学习，能够帮助大家巩固对链表数据结构特性的认知，同时强化基本的硬编码能力。

从下节开始，我们将用两个专题的时间，分解链表中的"不可爱"流派。接下来的学习或许不像本节一样轻松，但相信一定能给大家带来更重磅的收获~~

（阅读过程中有任何想法或疑问，或者单纯希望和笔者交个朋友啥的，欢迎大家添加我的微信xyalinode与我交流哈~）

快慢指针与多指针

链表题目中，有一类会涉及到反复的遍历 。涉及反复遍历的题目，题目本身虽然不会直接跟你说"你好，我是一道需要反复遍历的题目"，但只要你尝试用常规的思路分析它，你会发现它一定涉及反复遍历；同时，涉及反复遍历的题目，还有一个更明显的特征，就是它们往往会涉及相对复杂的链表操作，比如反转、指定位置的删除等等。

解决这类问题，我们用到的是双指针中的"快慢指针"。快慢指针指的是两个一前一后的指针，两个指针往同一个方向走，只是一个快一个慢。快慢指针严格来说只能有俩，不过实际做题中，可能会出现一前、一中、一后的三个指针，这种超过两个指针的解题方法也叫"多指针法"。

快慢指针+多指针，双管齐下，可以帮助我们解决链表中的大部分复杂操作问题。

快慢指针------删除链表的倒数第 N 个结点

真题描述：给定一个链表，删除链表的倒数第 n 个结点，并且返回链表的头结点。
示例：给定一个链表: 1->2->3->4->5, 和 n = 2.

当删除了倒数第二个结点后，链表变为 1->2->3->5.

说明：给定的 n 保证是有效的。

思路分析

小贴士：dummy 结点的使用

上一节我给大家介绍了 dummy 结点：它可以帮我们处理掉头结点为空的边界问题，帮助我们简化解题过程。因此涉及链表操作、尤其是涉及结点删除的题目（对前驱结点的存在性要求比较高），我都建议大家写代码的时候直接把 dummy 给用起来，建立好的编程习惯：

js 复制代码

const dummy = new ListNode()
// 这里的 head 是链表原有的第一个结点
dummy.next = head

"倒数"变"正数"

链表的删除我们上节已经讲过，相信都难不倒大家。这道题的难点实际在于这个"倒数第 N 个"如何定位。

考虑到咱们的遍历不可能从后往前走，因此这个"倒数第 N 个" 咱们完全可以转换为"正数第 len - n + 1"个。这里这个 len 代表链表的总长度，比如说咱们链表长为 7，那么倒数第 1 个就是正数第 7 个。按照这个思路往下分析，如果走直接遍历这条路，那么这个 len 就非常关键了。

我们可以直接遍历两趟：第一趟，设置一个变量 count = 0，每遍历到一个不为空的结点，count 就加 1，一直遍历到链表结束为止，得出链表的总长度 len；根据这个总长度，咱们就可以算出倒数第 n 个到底是正数第几个了（M = len - n + 1），那么我们遍历到第 M - 1（也就是 len - n）个结点的时候就可以停下来，执行删除操作（想一想，为什么是第 M-1 个，而不是第 M 个？如果你认真读了我们前面的章节，心中一定会有一个清晰的答案^_^）

不过这种超过一次的遍历必然需要引起我们的注意，我们应该主动去思考，"如果一次遍历来解决这个问题，我可以怎么做？"，这时候，就要请双指针法来帮忙了。

快慢指针登场

按照我们已经预告过的思路，首先两个指针 slow 和 fast，全部指向链表的起始位------dummy 结点：

快指针先出发！闷头走上 n 步，在第 n 个结点处打住，这里 n=2：

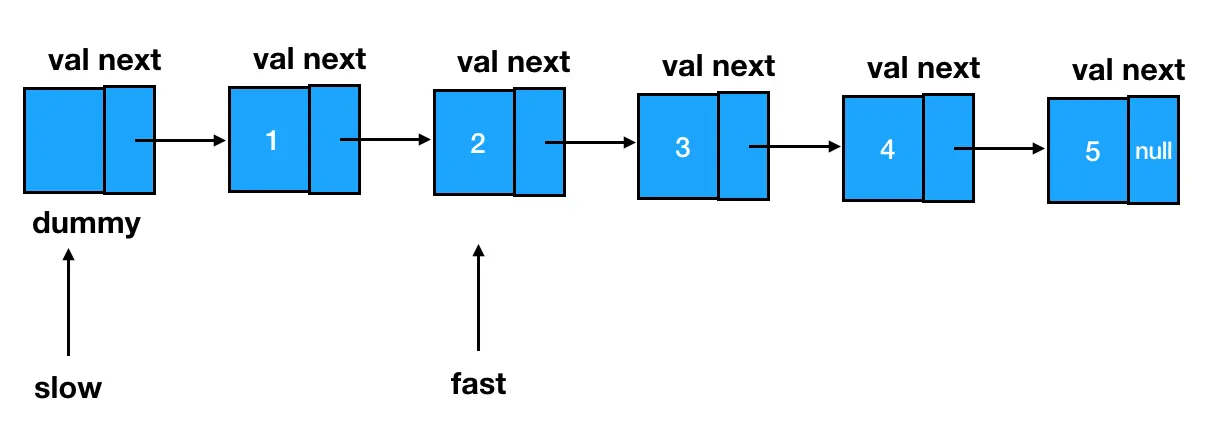然后，快慢指针一起前进，当快指针前进到最后一个结点处时，两个指针再一起停下来：

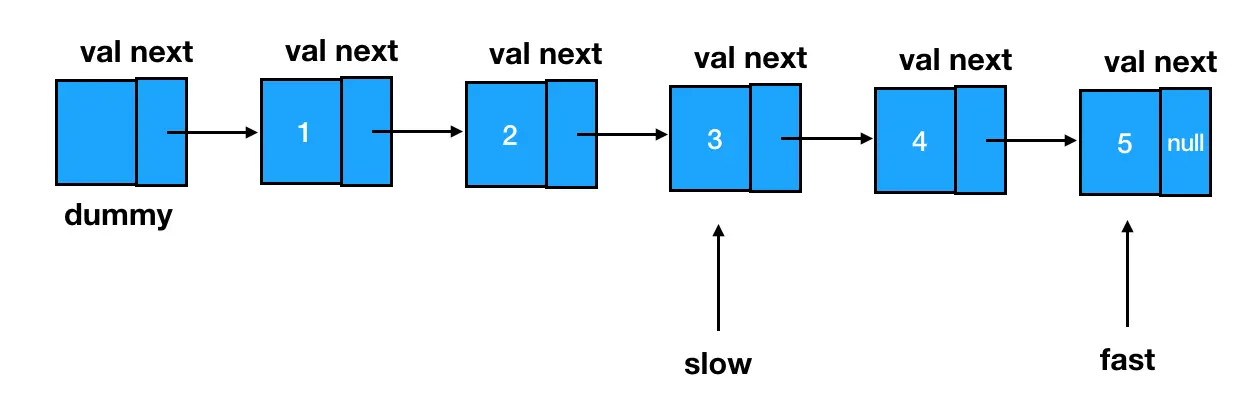此时，慢指针所指的位置，就是倒数第 n 个结点的前一个结点：

我们基于这个结点来做删除，可以说是手到擒来：

到这里，我们总结一下：

链表删除问题中，若走两次遍历，我们做了两件事：

1.求长度

2.做减法，找定位。

若用快慢指针，我们其实是把做减法和找定位这个过程给融合了。通过快指针先行一步、接着快慢指针一起前进这个操作，巧妙地把两个指针之间的差值保持在了"n"上（用空间换时间，本质上其实就是对关键信息进行提前记忆，这里咱们相当于用两个指针对差值实现了记忆 ），这样当快指针走到链表末尾（第 len 个）时，慢指针刚好就在 len - n 这个地方稳稳落地。

编码实现

js 复制代码

/**
 * @param {ListNode} head
 * @param {number} n
 * @return {ListNode}
 */
const removeNthFromEnd = function(head, n) {
    // 初始化 dummy 结点
    const dummy = new ListNode()
    // dummy指向头结点
    dummy.next = head
    // 初始化快慢指针，均指向dummy
    let fast = dummy
    let slow = dummy

    // 快指针闷头走 n 步
    while(n!==0){
        fast = fast.next
        n--
    }
    
    // 快慢指针一起走
    while(fast.next){
        fast = fast.next
        slow = slow.next
    }
    
    // 慢指针删除自己的后继结点
    slow.next = slow.next.next
    // 返回头结点
    return dummy.next
};

多指针法------链表的反转

完全反转一个链表

真题描述：定义一个函数，输入一个链表的头结点，反转该链表并输出反转后链表的头结点。
示例:

输入: 1->2->3->4->5->NULL

输出: 5->4->3->2->1->NULL

思路解读

这道题虽然是一道新题，但你要说你完全没思路，我真的哭了orz。老哥，我真想把这句话刻你显示器上------处理链表的本质，是处理链表结点之间的指针关系 。

我啥也不说，就给你一张链表的结构图：

来，你告诉我，我如何把这货颠倒个顺序呢？

是不是想办法把每个结点 next 指针的指向给反过来就行了：

你只要能想到这一步，就说明你对链表操作类题目已经有了最关键的感知，给你双击666~

接下来我们需要琢磨的是如何去反转指针的指向，这里我们需要用到三个指针，它们分别指向目标结点（cur）、目标结点的前驱结点（pre）、目标结点的后继结点（next）。这里咱们随便找个结点来开刀：

这里我只需要一个简单的cur.next = pre，就做到了 next 指针的反转：

有同学会说：那 next 不是完全没用到吗？

当然有用，你瞅瞅，咱们反转完链表变成啥样了：

这会儿我要是不用 next 给你指着 cur 原本的后继结点，你上哪去定位下一个结点呢？遍历都没法继续了嗷。

咱们从第一个结点开始，每个结点都给它进行一次 next 指针的反转。到最后一个结点时，整个链表就已经被我们彻底反转掉了。

编码实现

js 复制代码

/**
 * @param {ListNode} head
 * @return {ListNode}
 */
const reverseList = function(head) {
    // 初始化前驱结点为 null
    let pre = null;
    // 初始化目标结点为头结点
    let cur = head;
    // 只要目标结点不为 null，遍历就得继续
    while (cur !== null) {
        // 记录一下 next 结点
        let next = cur.next;
        // 反转指针
        cur.next = pre;
        // pre 往前走一步
        pre = cur;
        // cur往前走一步
        cur = next;
    }
    // 反转结束后，pre 就会变成新链表的头结点
    return pre
};

局部反转一个链表

反转链表真是座金矿，反转完整体反转局部，反转完局部还能每 k 个一组花式反转（最后这个略难，我们会放在真题训练环节来做）。虽然难度依次进阶，但只要把握住核心思想就没问题，下面咱们来看看如何反转局部：

真题描述：反转从位置 m 到 n 的链表。请使用一趟扫描完成反转。
说明: 1 ≤ m ≤ n ≤ 链表长度。
示例:

输入: 1->2->3->4->5->NULL, m = 2, n = 4

输出: 1->4->3->2->5->NULL

思路解读

我们仍然是从指针反转来入手：

按照题中的示例，假如我们需要反转的是链表的第 2-4 之间的结点，那么对应的指针逆序后会是这个样子：

4指3，3指2，这都没问题，关键在于，如何让1指向4、让2指向5呢？这就要求我们在单纯的重复"逆序"这个动作之外，还需要对被逆序的区间前后的两个结点做额外的处理：

由于我们遍历链表的顺序是从前往后遍历，那么为了避免结点1和结点2随着遍历向后推进被遗失，我们需要提前把1结点缓存下来。而结点5就没有这么麻烦了：随着遍历的进行，当我们完成了结点4的指针反转后，此时 cur 指针就恰好指在结点5上：

此时我们直接将结点2的 next 指针指向 cur、将结点1的 next 指针指向 pre 即可。

编码实现

js 复制代码

/**
 * @param {ListNode} head
 * @param {number} m
 * @param {number} n
 * @return {ListNode}
 */
// 入参是头结点、m、n
const reverseBetween = function(head, m, n) {
    // 定义pre、cur，用leftHead来承接整个区间的前驱结点
    let pre,cur,leftHead
    // 别忘了用 dummy 嗷
    const dummy = new ListNode()  
    // dummy后继结点是头结点
    dummy.next = head
    // p是一个游标，用于遍历，最初指向 dummy
    let p = dummy  
    // p往前走 m-1 步，走到整个区间的前驱结点处
    for(let i=0;i<m-1;i++){
        p = p.next
    }
    // 缓存这个前驱结点到 leftHead 里
    leftHead = p
    // start 是反转区间的第一个结点
    let start = leftHead.next  
    // pre 指向start
    pre = start
    // cur 指向 start 的下一个结点
    cur = pre.next
    // 开始重复反转动作
    for(let i=m;i<n;i++){
        let next = cur.next
        cur.next = pre
        pre = cur
        cur = next
    }
    //  leftHead 的后继结点此时为反转后的区间的第一个结点
    leftHead.next = pre
    // 将区间内反转后的最后一个结点 next 指向 cur
    start.next=cur
    // dummy.next 永远指向链表头结点
    return dummy.next
};

小贴士：楼上的两道反转题目，都可以用递归来实现，你试试？

（阅读过程中有任何想法或疑问，或者单纯希望和笔者交个朋友啥的，欢迎大家添加我的微信xyalinode与我交流哈~）

3 链表 二叉树

环形链表基本问题------如何判断链表是否成环？

思路解读

编码实现

环形链表衍生问题------定位环的起点

思路解读

编码实现

快慢指针的思路

弦外之音

典型真题快速上手-"有效括号"问题

思路分析

编码实现

栈问题进阶-每日温度问题

思路分析

编码实现

栈的设计------"最小栈"问题

思路分析

编码实现1

编码实现2

为什么一道题可以成为高频面试题

如何用栈实现一个队列？

思路分析

编码实现

认识双端队列

滑动窗口问题

思路分析：双指针+遍历法

编码实现：双指针+遍历法

解法复盘

思路分析：双端队列法

编码实现

深度优先搜索思想：不撞南墙不回头的"迷宫游戏"

深度优先搜索的本质------栈结构

DFS 与二叉树的遍历

广度优先搜索思想------找到迷宫出口的另一种思路

BFS实战：二叉树的层序遍历

结语

在开始之前

如何学好这一节

关键套路初相见：全排列问题

思路分析

编码实现

小贴士

组合问题：变化的"坑位"，不变的"套路"

思路分析

编码实现

编码复盘

限定组合问题：及时回溯，即为"剪枝"

思路分析

编码实现

概念复盘：何为"回溯"？

递归与回溯问题------解题模板总结

什么时候用

"遍历三兄弟"的迭代实现

从先序遍历说起

思路分析

编码实现

异曲同工的后序遍历迭代实现

思路分析

编码实现

思路清奇的中序遍历迭代实现

思路分析

编码实现

编码复盘

层序遍历的衍生问题

思路分析

编码实现

翻转二叉树

思路分析

编码实现

什么是二叉搜索树

二叉搜索树：编码基本功

查找数据域为某一特定值的结点

编码实现

插入新结点

编码实现

删除指定结点

编码实现

编码复盘

二叉搜索树的特性

真题实战环节