用A*算法在淄博某区域栅格影像图中寻找最优路径

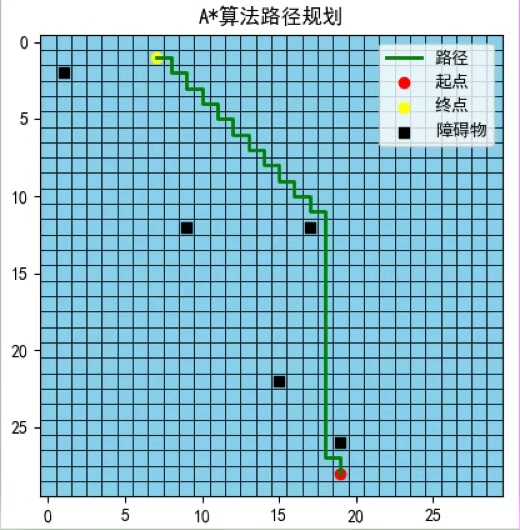
A*算法寻找最优路径python代码，从一点出发到达目标点的最优路径并展示，代码可运行。该算法为使用A算法寻找起点到终点的最优路径，同时设置了一系列障碍点，寻找的路径需避开障碍点。以淄博市某区域的栅格影像图为例，栅格像素值不同，代表的地物不同，根据地物设置每移动一步的代价也不同。 A算法是常用的静态环境路径规划算法之一，是Dijkstra算法与广度优先搜索算法结合的算法。通过借助启发式函数，A算法能够更快的找到最优路径。 A算法与Dijkstra算法流程相似，但也存在以下两点不同：（1）A算法使用启发函数来评估每个节点的"好坏"程度。节点的评估函数 f(n)如式1，综合考虑了从起始节点到当前节点的实际代价g(n) 和从当前节点到目标节点的估计代价h(n)，A算法选择具有最低评估值的节点进行探索，而Dijkstra算法只考虑从起始节点到当前节点的实际代价，并选择具有最低实际代价的节点进行探索。 f(n)=g(n) + h(n) (1) （2）A*算法通常需要存储每个节点的实际代价、估计代价和总评估值，而Dijkstra算法只需存储每个节点的实际代价。具体步骤如下： ①遍历当前节点的四个相邻栅格（上、下、左、右）。 ②对于每个相邻栅格，检查它是否在栅格地图内，且不是障碍物点。 ③如果相邻栅格在栅格地图内，且不是障碍物点，计算从起始位置到该邻居栅格的路径总成本：路径总成本=该邻居栅格到目标点的距离 + 每步的成本（在栅格地图中，每步的成本根据相邻栅格的像素值即地物类型确定）。 ④选择当前位置和各相邻节点中对应路径总成本最小的点作为下一步路径的方向，使得总成本最小。这样，算法在不断地选择最优路径，逐步接近目标位置，最终找到起点到目标点的最短路径。

在路径规划领域，A算法是个非常实用的存在，它结合了Dijkstra算法与广度优先搜索算法的优点，借助启发式函数能够快速找到最优路径。今天咱们就来看看如何用Python实现A算法，在淄博市某区域的栅格影像图里找到从一点到目标点的最优路径，并且避开障碍点。

A*算法基础原理

A*算法作为常用的静态环境路径规划算法，和Dijkstra算法流程有相似之处，但也存在关键不同。

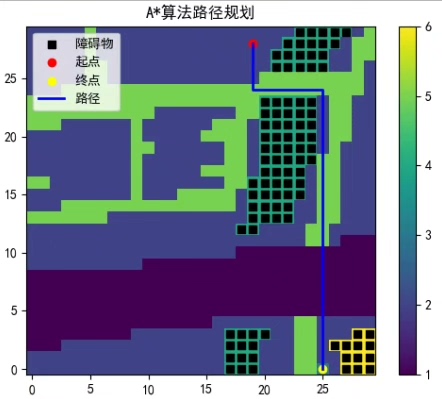
首先，A*算法使用启发函数评估每个节点的"好坏"程度。节点评估函数 $f(n)$ 综合考虑了从起始节点到当前节点的实际代价 $g(n)$ 和从当前节点到目标节点的估计代价 $h(n)$ ，即 $f(n)=g(n) + h(n)$ 。而Dijkstra算法只关注从起始节点到当前节点的实际代价。

其次，A*算法通常需要存储每个节点的实际代价、估计代价和总评估值，Dijkstra算法则只需存储实际代价。

算法具体步骤

遍历相邻栅格：遍历当前节点的四个相邻栅格（上、下、左、右）。
检查栅格合法性：对于每个相邻栅格，检查它是否在栅格地图内，且不是障碍物点。
计算路径总成本：如果相邻栅格合法，计算从起始位置到该邻居栅格的路径总成本：路径总成本 = 该邻居栅格到目标点的距离 + 每步的成本（在栅格地图中，每步的成本根据相邻栅格的像素值即地物类型确定）。
选择最优方向：选择当前位置和各相邻节点中对应路径总成本最小的点作为下一步路径的方向，使得总成本最小。通过不断重复这个过程，算法就能逐步接近目标位置，最终找到起点到目标点的最短路径。

Python代码实现

python 复制代码

import heapq
import math


def heuristic(a, b):
    return math.sqrt((b[0] - a[0]) ** 2 + (b[1] - a[1]) ** 2)


def astar(array, start, goal):
    # 优先队列，存放待扩展节点，按照f值从小到大排序
    open_set = []
    heapq.heappush(open_set, (0, start))
    came_from = {}
    g_score = {node: float('inf') for row in array for node in row}
    g_score[start] = 0
    f_score = {node: float('inf') for row in array for node in row}
    f_score[start] = heuristic(start, goal)

    while open_set:
        _, current = heapq.heappop(open_set)

        if current == goal:
            path = []
            while current in came_from:
                path.append(current)
                current = came_from[current]
            path.append(start)
            path.reverse()
            return path

        for neighbor in [(0, 1), (0, -1), (1, 0), (-1, 0)]:
            neighbor_node = (current[0] + neighbor[0], current[1] + neighbor[1])
            if 0 <= neighbor_node[0] < len(array) and 0 <= neighbor_node[1] < len(array[0]) and \
                    array[neighbor_node[0]][neighbor_node[1]]!= 1:
                tentative_g_score = g_score[current] + 1
                if tentative_g_score < g_score[neighbor_node]:
                    came_from[neighbor_node] = current
                    g_score[neighbor_node] = tentative_g_score
                    f_score[neighbor_node] = tentative_g_score + heuristic(neighbor_node, goal)
                    if neighbor_node not in [i[1] for i in open_set]:
                        heapq.heappush(open_set, (f_score[neighbor_node], neighbor_node))
    return None


# 简单示例栅格地图，0代表可通行，1代表障碍物
grid = [[0, 0, 0, 0],
        [0, 1, 0, 0],
        [0, 0, 0, 0],
        [0, 0, 0, 0]]
start = (0, 0)
goal = (3, 3)
path = astar(grid, start, goal)
print(path)

代码分析

heuristic函数：这个函数计算的是启发式距离，这里用的是欧几里得距离，也就是从当前点到目标点的直线距离估计。通过这个函数，A*算法能大致知道往哪个方向走更接近目标。
astar函数 ：这是核心的A*算法实现部分。
- 初始化 ：openset**是一个优先队列，用来存放待扩展的节点，按照节点的 f 值从小到大排序。came from 字典记录每个节点是从哪个节点过来的，方便最后回溯路径。gscore**记录从起点到每个节点的实际代价，初始都设为无穷大，起点的 g score 为0。fscore**记录每个节点的评估值 f(n)，同样初始化为无穷大，起点的 f score 由启发式函数计算得到。
- 主循环 ：不断从 openset**中取出 f 值最小的节点 current。如果这个节点就是目标节点，那就通过 came from 回溯得到完整路径并返回。
- 遍历邻居 ：对当前节点的四个邻居（上下左右）进行检查。如果邻居在栅格地图内且不是障碍物（这里简单用值1表示障碍物），就计算从起点到这个邻居的暂定 gscore*。如果这个暂定 g* score 比之前记录的这个邻居的 gscore**小，就更新 came from、gscore**和 f score，并把这个邻居加入 open_set。

这样，我们就实现了一个简单的A*算法，能在有障碍物的栅格地图中找到从起点到终点的最优路径啦，在实际应用中可以根据淄博市某区域栅格影像图的具体地物和代价设置来灵活调整代码。