33 Continuous State Spaces (DQN)
33.1 Example of Continuous State Applications
之前举例的简化版火星探测器的状态只有位置,且只可能是6个离散的值。实际场景中,状态往往是一个向量,且其中的每个值可能是离散的,也可能有连续的
33.2 Example: Lunar Lander
为了介绍算法,我们以简化的月球着陆器为例进行说明
状态我们考虑8个值,分别是x和y表示位置,以及两个维度上的速度,以及角度和角速度,最后用l和r表示左右脚是否接触到月球表面(二值变量,只能是0或1)
那么状态向量s表示为:s⃗=[xyx˙y˙θθ˙lr]\vec s = \left[ \begin{array}{c} x \\ y \\ \dot{x} \\ \dot{y} \\ \theta \\ \dot{\theta} \\ l \\ r \end{array} \right]s = xyx˙y˙θθ˙lr
注:前6个为连续值,l和r为离散值,可以放在一起
另外,假设只有4种动作:
- None,不操作,自由落体
- left,启动左引擎
- main,启动主引擎
- right,启动右引擎
然后,我们定义可以一些奖励函数:

例如,软着陆奖励高额正分,坠毁进行高额负奖励,还可以为了鼓励节约燃料,给启动引擎小额的负分奖励
33.3 Learning the State-action Value Function
接下来,我们可以用神经网络学习状态-动作值函数
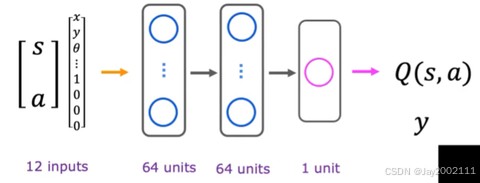
输入是s和a拼接起来的向量。前面提到4种动作,用独热编码,对应有4个0/1值的独热特征向量,和s拼接起来总共是12个值的输入,最后的输出是预测的Q(s, a)
接下来用监督学习,需要用到若干个训练样本,每个训练样本是 状态-动作对(即x) 到 Q(s,a)(即y) 的映射,我们将使用贝尔曼方程来创建足量的训练样本
先回顾一下贝尔曼方程:
Q(s,a)=R(s)+γmaxa′Q(s′,a′)Q(s, a) = R(s) + \gamma \max_{a'}Q(s', a')Q(s,a)=R(s)+γa′maxQ(s′,a′)
明确一下问题,s和a即为输入x,而贝尔曼方程的即为y,神经网络是关于W, B的函数f,目标是让fW,B(x)≈yf_{W, B}(x) \approx yfW,B(x)≈y。现在,我们将月球探测器进行若干次随机的操作,即可得到若干个元组(s,a,R(s),s′)(s, a, R(s), s')(s,a,R(s),s′),取其中的s和a即可得到输入x
接下来的问题是如何每个x对应的y呢?代入贝尔曼方程计算Q(s, a),方程右侧的Q(s', a')我们用当前的神经网络计算 ,一开始因为是随机化的参数,所以输出的Q当然也是随机的,但是事实证明随着训练的进行,这个神经网络的输出Q函数可以越来越好 ,算出最大的Q(s', a')代入方程得到y,之后每一轮神经网络参数的迭代,我们要更新y的值
基本流程:
随机初始化神经网络的参数,猜测Q(s, a)
Repeat {
按某种策略(ε-贪婪策略,后续介绍)操作月球探测器,得到(s, a, R(s), s')
存储最近的若干个(s, a, R(s), s')元组(例如10000个,这种仅存储最近的示例的技术被称作"Replay Buffer"(重放缓冲区))
训练神经网络:
随机抽取Replay Buffer中的batch_size个元组,创建训练样本x, y
训练出Q_new(s, a)≈y
Q=QnewQ = Q_{new}Q=Qnew
}
注:
- 这个算法被称为DQN(Deep Q-Network,深度Q网络),是一种基于深度学习的强化学习算法。它通过使用神经网络来学习Q值函数
- Replay Buffer重放缓冲区又称经验回放缓冲区 ,经验回放机制通过将智能体与环境的交互经验 (s,a,R(a),s′)(s, a, R(a), s')(s,a,R(a),s′) 存储在一个缓冲区中,然后从中随机抽取批量样本的输入并构造输出进行训练。这样做的目的是打破连续经验之间的时间相关性,让神经网络的训练数据更接近独立同分布(i.i.d.),从而极大地提高训练的稳定性和数据利用效率
33.4 Algorithm Refinement: Improved Neural Network Architecture
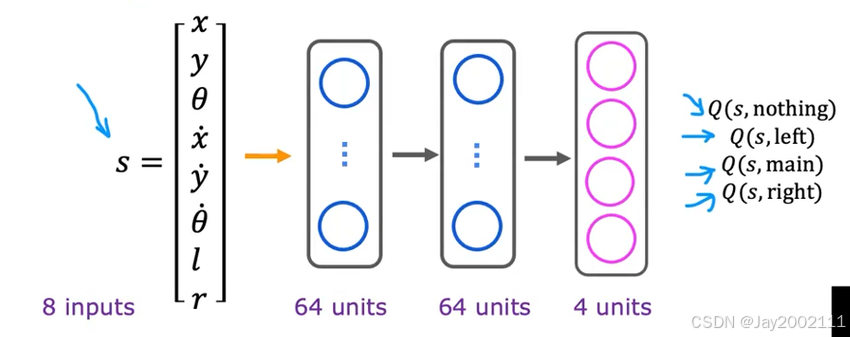
前面的神经网络架构最后只有一个输出,我们可以改为N个输出,每个输出对应一个动作
这时神经网络的输入将不再是s和a,而是只有s,预测的就是maxaQ(s,a)\max_{a}Q(s, a)maxaQ(s,a)
33.5 Algorithm Refinement: ε-Greedy Policy
ε-Greedy Policy(ε-贪婪策略)是强化学习中最常用、最基本的动作选择策略之一,用于在智能体的探索(Exploration)和利用(Exploitation)之间找到平衡
在强化学习中,智能体面临一个持续的困境:
- 利用 (Exploitation): 基于当前已知的最佳信息,选择当前价值最高的动作,这能最大化短期回报
- 探索 (Exploration): 尝试那些价值未知或当前估计价值较低的动作,以期发现潜在的、更好的动作,这是找到全局最优解的关键
如果智能体只进行利用,它可能会陷入局部最优 。如果只进行探索,它会浪费大量时间在已知的次优动作上
ε-Greedy 核心在于一个参数 ϵ\epsilonϵ(epsilon,一个介于 0 到 1 之间的概率值),在每一个决策步骤,智能体执行以下操作:
- 以概率 1−ϵ1 - \epsilon1−ϵ 进行利用:
- 智能体选择当前估计价值最高的动作(贪婪选择)
- 例如,在 DQN 中,选择 a∗=argmaxaQ(s,a)a^* = \arg \max_{a} Q(s, a)a∗=argmaxaQ(s,a)
- 以概率 ϵ\epsilonϵ 进行探索:
- 智能体随机地从所有可能的动作中选择一个动作
- 这使得智能体能够尝试新的、甚至看起来不好的动作,收集更多信息
注:在实际应用中,尤其是像 DQN 这样的算法,ϵ\epsilonϵ通常不是一个固定的值,而是会随着训练的进行而逐渐衰减 ,被称为ϵ\epsilonϵ衰减(Epsilon Decay)
33.6 Algorithm Refinement: Mini-batch and Soft Update
批量梯度下降(Mini-batch Gradient Descent) 是一种优化算法中数据处理的技术,目的是在训练深度神经网络时,兼顾效率和稳定性
在训练神经网络时,一次梯度下降更新的计算涉及到的样本集合被称为一个批次(Batch) 。Mini-batch 梯度下降是介于 随机梯度下降(Stochastic Gradient Descent, SGD) 和 全批量梯度下降(Batch Gradient Descent, BGD) 之间的一种折衷方案
全批量梯度下降使用全部样本计算梯度并更新参数,而随机梯度下降随机抽取1个样本计算梯度并更新参数,而批量梯度下降是每次迭代从全部训练样本中随机抽取一个大小为batch_size的小批量(Mini-batch)样本 来计算梯度并更新参数,可以获得比 SGD 更稳定的梯度估计,同时保持比 BGD 更快的训练速度和更低的计算成本
之前描述的DQN过程中,每一步训练后立即复制当前网络的最新参数Q=QnewQ = Q_{new}Q=Qnew,但如果碰巧遇到这个新的参数效果并不好,网络将会直接变差。这种硬更新的方式会使训练过程剧烈震荡、难以收敛,甚至参数发散,训练失败
进一步,我们可以考虑每隔C步更新一次网络参数,即周期硬更新 。在这C步的学习周期内,网络参数保持固定,因此用于计算目标值y的项也是固定的,有C次梯度下降的机会来稳定地拟合一个固定的目标,极大地提高了训练的稳定性。但在第C步时,网络参数仍将跳变,可能在训练曲线上表现为周期性的震荡或抖动,但整体趋势是稳定的。这种方式仍存在周期性震荡的缺点
Soft Update(软更新) 是一种更平滑、更连续的网络更新方法。注意,这里不需要周期,即每一步训练都更新网络参数。软更新的核心是更新网络参数时不是直接赋值新参数,而是让旧参数以极小的速率向新参数更新,这个速率一般用字母τ\tauτ来表示,例如神经网络的参数W和B,采用软更新:
W=τWnew+(1−τ)WB=τBnew+(1−τ)B\begin{aligned} W &= \tau W_{new} + (1 - \tau)W\\ B &= \tau B_{new} + (1 - \tau)B \end{aligned}WB=τWnew+(1−τ)W=τBnew+(1−τ)B
33.7 Summary of DQN Algorithm
前面描述的DQN算法流程不够准确,结合介绍的优化步骤,重新梳理一下DQN的流程
先定义一下参数:N为离散动作空间的大小(即网络的输出维度,动作的种类数量),M为Mini-batch的大小,C为周期硬更新的间隔(目标网络同步频率),k用来给学习步数计数,Y表示目标输出(即"标准答案")
前面我们用W和B代表神经网络参数,后续统一用θ\thetaθ表示网络参数
DQN的核心是经验回放和目标网络 。重点阐述一下当前网络 和目标网络:
当前 Q 网络(Online Q-Network) Q(θ)Q(\theta)Q(θ)是智能体的主要学习和决策结构,它的参数θ\thetaθ在每一步训练中都通过梯度下降进行实时更新。该网络承担两个核心职责:
- 动作选择 : 用于在当前状态s下预测所有动作的Q值,并根据ϵ\epsilonϵ-贪婪策略决定下一步的动作
- 当前估计 : 用于计算损失函数中的预测值 Q(s,a;θ)Q(s, a; \theta)Q(s,a;θ)
目标 Q 网络(Target Q-Network) Q(θ−)Q(\theta^-)Q(θ−)是一个结构与当前网络相同的复制品,其参数θ−\theta^-θ−专门用于计算 Bellman 方程中的稳定目标值,即暂时当作是标准答案的Y。为了确保Y的稳定,θ−\theta^-θ−不会实时更新,而是每隔C个学习步才从当前网络周期性地复制一次。目标网络通过解耦学习目标,避免了网络训练中"追逐自己的尾巴"的问题,是保障 DQN 训练稳定收敛的关键机制
注:总结一下,当前网络是一直在学习的网络,目标网络是当做标准答案计算Y的那个网络,每隔C步从当前网络复制一次,目标网络周期性更新是为了确保目标值的稳定
接下来,详细阐述DQN的流程:
- 随机初始化:
- 初始化参数 θ\thetaθ 和 θ−\theta^-θ−。
- 初始化空的 Replay Buffer
- 初始化ϵ\epsilonϵ衰减计划(例如从1.0递减到0.01)
- 主循环(环境交互与学习,进行T次,例如T=107T=10^7T=107)
- 数据收集与存储 (执行 1 次):用ε-Greedy策略,选择动作并执行,将(s, a, R(s), s')存入Replay Buffer,并衰减ε
- 直到Replay Buffer的元组数量大于等于M,执行后续操作,否则不执行
- 网络学习与更新 (通常执行 1 次):
- 计数器 k=k+1k = k + 1k=k+1
- Mini-batch 采样,随机采样M个
- 计算M个样本的目标值Y,用目标网络Q(θ−)Q(\theta^-)Q(θ−)计算
- 计算损失:L(θ)=∑i=1M(Yi−Q(si,ai;θ))2L(\theta) = \sum_{i=1}^{M} (Y_i - Q(s_i, a_i; \theta))^2L(θ)=∑i=1M(Yi−Q(si,ai;θ))2
- 使用优化器最小化 L(θ)L(\theta)L(θ),更新当前网络 θ\thetaθ
- 目标网络同步:如果 k mod C=0k \bmod C = 0kmodC=0,则θ−←θ\theta^- \leftarrow \thetaθ−←θ(硬更新),如果是软更新,则不用隔C步,每步都更新θ−←τθ+(1−τ)θ−\theta^- \leftarrow \tau \theta + (1 - \tau) \theta^-θ−←τθ+(1−τ)θ−(软更新)
注:软更新只应用在目标网络的参数上;当前网络(online network)参数照常用梯度下降每步更新