• 核心理论 (Core Theory)
◦ 拉格朗日函数 (Lagrangian): 通过引入拉格朗日乘子,将一个带约束问题转化为一个无约束的函数,是连接原始问题和对偶问题的桥梁。
◦ KKT 条件 (Karush-Kuhn-Tucker Conditions): 这是约束优化最优性条件的"黄金标准",它将拉格朗日乘子法推广到了包含不等式约束的一般情况。它包含四个部分:
▪ 驻点性 (Stationarity)
▪ 原始可行性 (Primal Feasibility)
▪ 对偶可行性 (Dual Feasibility)
▪ 互补松弛性 (Complementarity)
◦ 对偶性 (Duality): 通过构造对偶问题,为原始问题提供一个下界(弱对偶),在某些条件下甚至可以得到与原始问题相同的解(强对偶),从而开辟了全新的求解路径。
• 核心算法 (Core Algorithms)
◦ 投影梯度法 (Projected Gradient Method): 梯度下降法在约束问题上的直接推广,适用于可行集结构简单、投影计算廉价的场景。
◦ 交替方向乘子法 (ADMM): 一个强大的分解协调算法,特别适用于目标函数或约束具有可分离结构的复杂大规模问题,在分布式计算和现代机器学习中扮演着重要角色。
• 应用 (Application)
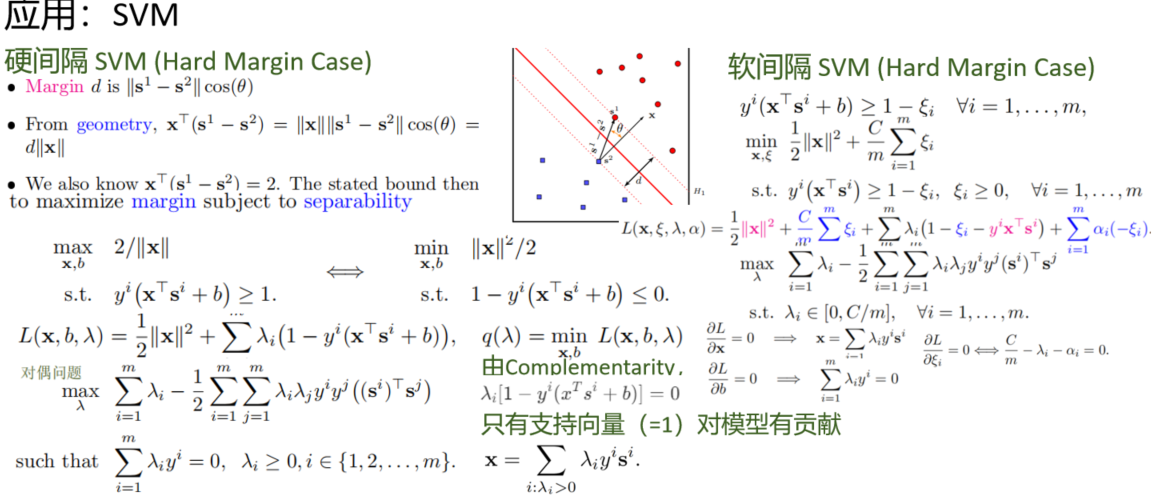
◦ 支持向量机 (Support Vector Machines, SVM): 作为一个经典的机器学习模型,SVM的推导和求解完美地展示了KKT条件和对偶理论的强大威力。
一、 KKT 条件 (Karush-Kuhn-Tucker Condition)


二、 案例:支持向量机
三、 投影梯度法 (Projected Gradient Method)

四、 交替方向乘子法 (Alternating Direction Method of Multipliers)

