《python语言程序设计》2018版 第8章第215页第47行有误

第8章第20的题面

Rational代码
python
class Rational:
def __init__(self, numerator=1, denominator=0):
divisor = gcd(numerator, denominator)
self.__numerator = (1 if denominator > 0 else -1) * int(numerator / divisor)
self.__denominator = int(abs(denominator) / divisor)
def __add__(self, second_rational):
n = (
self.__numerator * second_rational[1]
+ self.__denominator * second_rational[0]
)
d = self.__denominator * second_rational[1]
return Rational(n, d)
def __sub__(self, second_rational):
n = (
self.__numerator * second_rational[1]
self.__denominator * second_rational[0]
)
d = self.__denominator * second_rational[1]
return Rational(n, d)
def __mul__(self, second_rational):
n = self.__numerator * second_rational[0]
d = self.__denominator * second_rational[1]
return Rational(n, d)
def __truediv__(self, second_rational):
n = self.__numerator * second_rational[1]
d = self.__denominator * second_rational[0]
return Rational(n, d)
def __float__(self):
return self.__numerator / self.__denominator
def __int__(self):
return int(self.__float__())
def __str__(self):
if self.__denominator == 1:
return str(self.__numerator)
else:
return str(self.__numerator) + "/", self.__denominator
def __lt__(self, second_rational): #小于
return self.__lt__(second_rational) < 0
def __le__(self, second_rational):#大于
return self.__le__(second_rational) <= 0
def __gt__(self, second_rational):
return self.__gt__(second_rational) > 0
def __ge__(self, second_rational):
return self.__ge__(second_rational) >= 0
def __cmp__(self, second_rational):
temp = self.__sub__(second_rational)
if temp[0] > 0:
return 1
elif temp[0] < 0:
return -1
else:
return 0
def __getitem__(self, index):
if index == 0:
return self.__numerator
else:
return self.__denominator
def gcd(n, d):
n1 = abs(n)
n2 = abs(d)
gcd = 1
k = 1
while k <= n1 and k <= n2:
if n1 % k == 0 and n2 % k == 0:
gcd = k
k += 1
return gcd名词解释
| 英文 | 汉语 | 作用 | 特点 |
|---|---|---|---|
| Rational | 有理数 | 一般用Rational类来处理分数运算 | 可以避免浮点数精度丢失 |
| numerator | 分子 | ||
| denominator | 分母 | 编程中需注意分母不能为 0 | |
| divisor | 除数 | 约数 | |
| gcd | Greatest Common Divisor | 最大公约数 / 最大公因数 | 1. 数学定义:能同时整除两个(或多个)整数的最大正整数(如 12 和 18 的 gcd 是 6);2. 编程用法:Python 中通过 math.gcd() 函数实现,需注意:- 仅接受非负整数,且返回值≥1; 若输入 0 和非 0 数,返回非 0 数(如 gcd (0,8)=8);3. 核心用途:化简分数(分子分母同除以 gcd,得到最简分数)。 |
用语言来形容
建立Rational类
建立初始化函数__init__(内含self, 分子=1,分母=0)
在函数中放变量整除(divisor) ,内含gcd(分子,分母)
指定私有域numerator 范围是
疑难名句
self.__numerator = (1 if denominator > 0 else -1) * int(numerator / divisor)
1 if denominator > 0 else -1 是「一行式的条件判断」,核心作用是快速获取分母的符号因子,常用于分数 / 有理数的符号标准化,等价于普通 if-else 但更简洁。
自定义的重载运算符
在本程序Rational类中的__ge__
python
def __ge__(self, second_rational):
return self.__ge__(second_rational) >= 0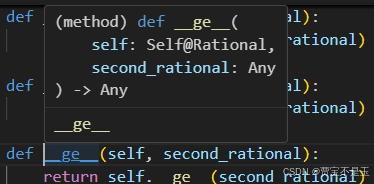
默认代码中的__ge__

默认的__ge__它趋向的bool
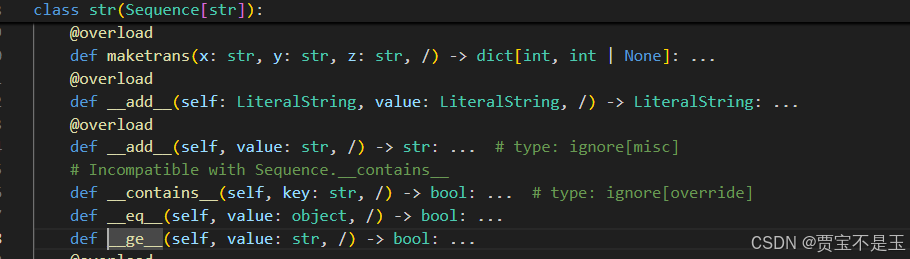
python中class str类的__ge__
Rational代码 我最无法理解的部分 ^[1](#Rational代码 我最无法理解的部分 1 2)^ ^[2](#Rational代码 我最无法理解的部分 1 2)^
python
class Rational:
def __init__(self, numerator=1, denominator=0):
# 详见gcd最大公约数--《python语言程序设计》2018版--第8章20题使用Rational类求和数列
divisor = gcd(numerator, denominator)
# 详见三元表达式《python语言程序设计》2018版--第8章20题分支
self.__numerator = (1 if denominator > 0 else -1) * int(numerator / divisor)
self.__denominator = int(abs(denominator) / divisor)错误初尝试TypeError:str returned non-string(type tuple)

python
def __str__(self):
if self.__denominator == 1:
return str(self.__numerator)
else:
return str(self.__numerator) + "/", self.__denominator #错了
def main_test():
a = 1
b = 2
c = Rational(1,2)
print(c)
main_test()return str(self.__numerator) + "/", self.__denominator 实际返回的是元组(tuple)(格式:("分子/", 分母)),而非字符串;
修改一下,问题照旧???

+ "/",大家注意看一下是不是应该两边都是+号呢?
return str(self.__numerator) + "/", str(self.__denominator)
重新修改
python
def __str__(self):
if self.__denominator == 1:
return str(self.__numerator)
else:
return str(self.__numerator) + "/"+ str(self.__denominator)
def main_test():
a = 1
b = 2
c = Rational(1,2)
print(c)
main_test() return f"分子{self.__numerator} 和分母{self.__denominator}和return str(self.__numerator) + "/" + str(self.__denominator)的不同结果
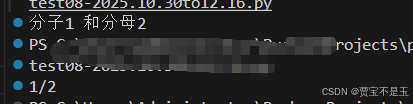
同时注意