正则化笔记 - 技术栈

正则化Regularization

机器学习训练模型时，在损失函数中增加额外项，用于惩罚过大的参数，可用于限制模型复杂度、避免过拟合、提高模型泛化能力

L1正则化（Lasso回归）

在损失函数中加入参数的绝对值之和，公式如下：
LossL1=原先Loss+λ∑i=1k∣ωi∣ Loss_{L1}=原先Loss+\lambda \sum_{i=1}^{k} \mid \omega_i \mid LossL1=原先Loss+λi=1∑k∣ωi∣

L1正则化通过惩罚模型参数的绝对值，使得部分权重趋近0甚至变为0，模型会自动丢弃一些不重要的特征。λ超参数控制着正则化的强度，较大的λ值意味着强烈的正则化，会使得模型更简单（可能会导致欠拟合），较小的λ会使模型更复杂，可能导致过拟合。

L2正则化（Ridge回归、岭回归）

L2正则化在损失函数中加入参数的平方之和：
LossL2=原先Loss+λ∑i=1kωi2 Loss_{L2}=原先Loss+\lambda \sum_{i=1}^{k} \omega_i^2 LossL2=原先Loss+λi=1∑kωi2

L2正则化通过惩罚模型参数的平方，使得所有参数都变得更小（0.01的参数，平方之后，变成0.0001），但是不会将参数强行压缩为0，会使得模型尽量平滑，防止过拟合。

ElasticNet正则化（弹性网络回归）

ElasticNet正则化结合了L1和L2正则化，通过调整两个正则化项的比例来取得平衡，使得同时具备稀疏性和稳定性的优点：
LossElasticNet=原先Loss+λ(α∑i=1n∣ωi∣+1−a2∑i=1nωi2)其中：α∈ $0,1$ ，决定L1和L2的权重 Loss_{ElasticNet}=原先Loss+\lambda(\alpha \sum_{i=1}^{n}\mid\omega_i\mid+\frac{1-a}{2}\sum_{i=1}^{n} \omega_i^2) \\ 其中：\\ \alpha\in $0,1$ ，决定L1和L2的权重 LossElasticNet=原先Loss+λ(αi=1∑n∣ωi∣+21−ai=1∑nωi2)其中：α∈ $0,1$ ，决定L1和L2的权重

代码验证

python 复制代码

import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split  # 划分训练集和测试集
from sklearn.linear_model import LinearRegression, Lasso, Ridge  # 线性回归模型, Lasso回归, Ridge回归
from sklearn.preprocessing import PolynomialFeatures  # 构建多项式特征
from sklearn.metrics import mean_squared_error  # 均方误差损失函数

'''
1. 生成数据
2. 划分训练集和测试集（验证集）
3. 定义模型（线性回归模型）
4. 训练模型
5. 预测结果，计算误差
'''

plt.rcParams['font.sans-serif']=['KaiTi']
plt.rcParams['axes.unicode_minus']=False

# 1. 生成数据
X = np.linspace(-3, 3, 300).reshape(-1, 1)
# print("X: \n{}".format(X))
print("X.shape: \n{}".format(X.shape))
y = np.sin(X) + np.random.uniform(low=-0.5, high=0.5, size=300).reshape(-1, 1)
print("y.shape: \n{}".format(y.shape))

# 画出散点图
fig, ax = plt.subplots(2, 3, figsize=(15, 8))
ax[0, 0].scatter(X, y, c="y")
ax[0, 1].scatter(X, y, c="y")
ax[0, 2].scatter(X, y, c="y")
# plt.show()

# 2. 划分训练集和测试集（验证集）
trainX, textX, trainY, textY = train_test_split(X, y, test_size=0.2, random_state=42)

# 过拟合（20次）
poly20 = PolynomialFeatures(degree=20)
x_train = poly20.fit_transform(trainX)
x_text = poly20.fit_transform(textX)

# 一、不加正则化项
# 3. 定义模型
model = LinearRegression()

# 4. 训练模型
model.fit(x_train, trainY)

# 5. 预测结果，计算误差
y_pred1 = model.predict(x_text)
test_loss1 = mean_squared_error(textY, y_pred1)
# train_loss = mean_squared_error(trainY, model.predict(x_train))

# 画出拟合曲线，并写出训练误差和测试误差
ax[0, 0].plot(X, model.predict(poly20.fit_transform(X)), "r")
ax[0, 0].text(-3, 1, f"测试误差：{test_loss1:.4f}")
# ax[0, 2].text(-3, 1.3, f"训练误差：{train_loss:.4f}")

# 画出所有系数的直方图
ax[1, 0].bar(np.arange(21), model.coef_.reshape(-1))

# 二、Lasso回归
lasso = Lasso(alpha=0.01)

# 4. 训练模型
lasso.fit(x_train, trainY)

# 5. 预测结果，计算误差
y_pred1 = lasso.predict(x_text)
test_loss1 = mean_squared_error(textY, y_pred1)
# train_loss = mean_squared_error(trainY, model.predict(x_train))

# 画出拟合曲线，并写出训练误差和测试误差
ax[0, 1].plot(X, lasso.predict(poly20.fit_transform(X)), "r")
ax[0, 1].text(-3, 1, f"测试误差：{test_loss1:.4f}")
# ax[0, 2].text(-3, 1.3, f"训练误差：{train_loss:.4f}")

# 画出所有系数的直方图
ax[1, 1].bar(np.arange(21), lasso.coef_.reshape(-1))

# 三、Ridge回归
ridge = Ridge(alpha=1)

# 4. 训练模型
ridge.fit(x_train, trainY)

# 5. 预测结果，计算误差
y_pred3 = ridge.predict(x_text)
test_loss3 = mean_squared_error(textY, y_pred3)
# train_loss = mean_squared_error(trainY, model.predict(x_train))

# 画出拟合曲线，并写出训练误差和测试误差
ax[0, 2].plot(X, ridge.predict(poly20.fit_transform(X)), "r")
ax[0, 2].text(-3, 1, f"测试误差：{test_loss3:.4f}")
# ax[0, 2].text(-3, 1.3, f"训练误差：{train_loss:.4f}")

# 画出所有系数的直方图
ax[1, 2].bar(np.arange(21), ridge.coef_.reshape(-1))

plt.show()

运行结果：

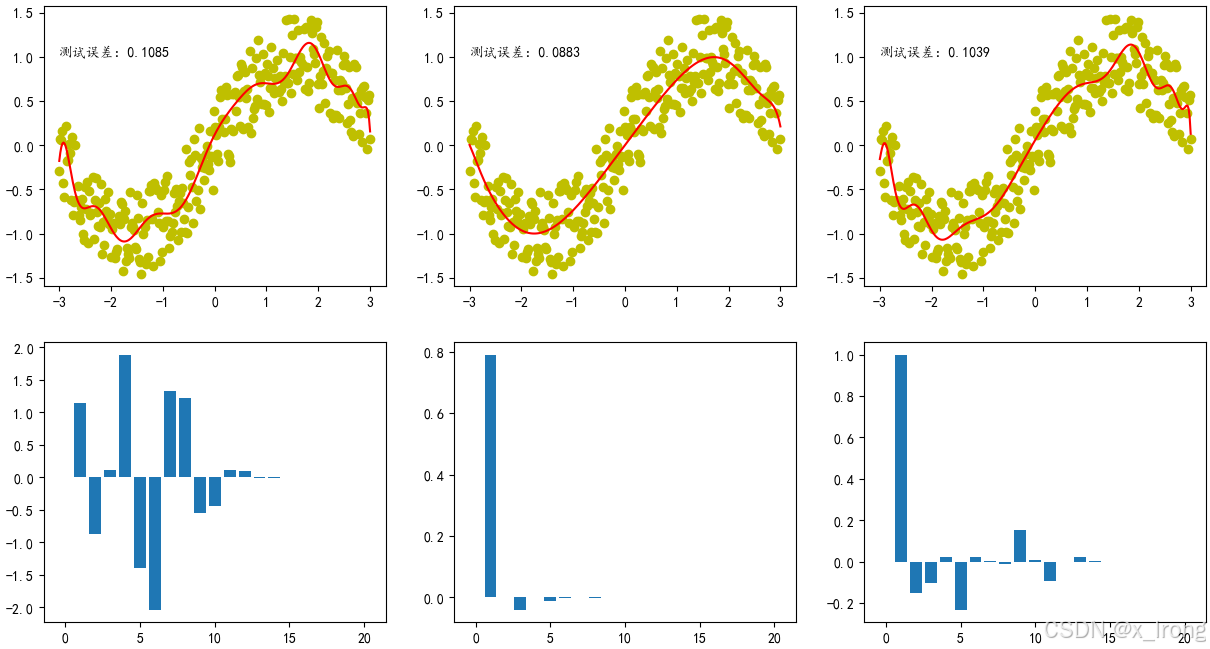
出所有系数的直方图

ax $1, 2$ .bar(np.arange(21), ridge.coef_.reshape(-1))

plt.show()

复制代码

[外链图片转存中...(img-0w3djrDt-1765972243937)]

###