代码随想录 463.岛屿的周长

思路：

1.网格问题：网格问题是这样的一类搜索问题：由m×n个小方格组成一个网格，每个小方格与其上下左右的四个方格被认为是相邻的，要在这样的网格上进行某种搜索。这种题目用DFS实现会非常简单。

2.如何构造方格类DFS的代码？

（1）首先，每个方格与其上下左右的四个方格相邻，则DFS每次要分出四个岔。

java 复制代码

// 基本的 DFS 框架：每次搜索四个相邻方格
void dfs(int[][] grid, int r, int c) {
    dfs(grid, r - 1, c); // 上边相邻
    dfs(grid, r + 1, c); // 下边相邻
    dfs(grid, r, c - 1); // 左边相邻
    dfs(grid, r, c + 1); // 右边相邻
}

（2）但是，对于网格边缘的方格，上下左右并不都有邻居。

思路一：在递归调用之前判断方格的位置，例如位于左边缘则不访问其左邻居。但这样一个一个判断写起来会比较麻烦。（×）

思路二：采用"先污染后治理"的思路，先做递归调用，再在每个DFS函数的开头判断其是否合法，不合法的直接返回。同样，还需要判断该方格是否有岛屿（值是否为1），否则也需要返回。（√）

java 复制代码

// 处理方格位于网格边缘的情况
void dfs(int[][] grid, int r, int c) {
    // 若坐标不合法，直接返回
    if (!(0 <= r && r < grid.length && 0 <= c && c < grid[0].length)) {
        return;
    }
    // 若该方格不是岛屿，直接返回
    if (grid[r][c] != 1) {
        return;
    }
    dfs(grid, r - 1, c);
    dfs(grid, r + 1, c);
    dfs(grid, r, c - 1);
    dfs(grid, r, c + 1);
}

（3）但这样还有一个问题，那就是DFS可能会不停地兜圈子，永远停不下来，如下图所示。

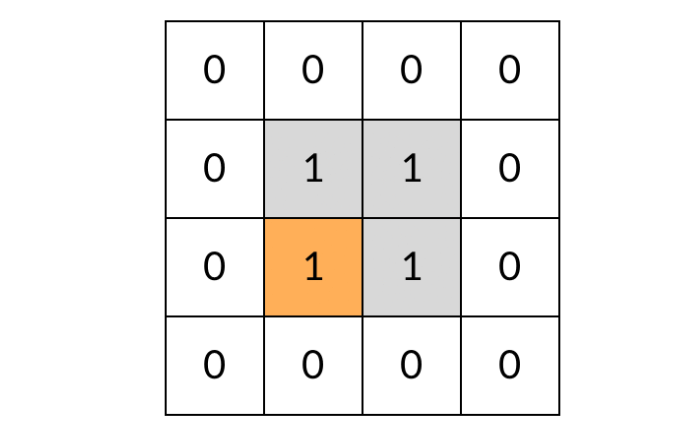
（4）那么我们需要标记遍历过的方格，保证方格不进行重复遍历。标记遍历过的方格并不需要使用额外空间，只需要改变方格中存储的值就可以。在这道题中，值为0表示非岛屿（不可遍历），值为1表示岛屿（可遍历），可以用2表示已经遍历过的岛屿。

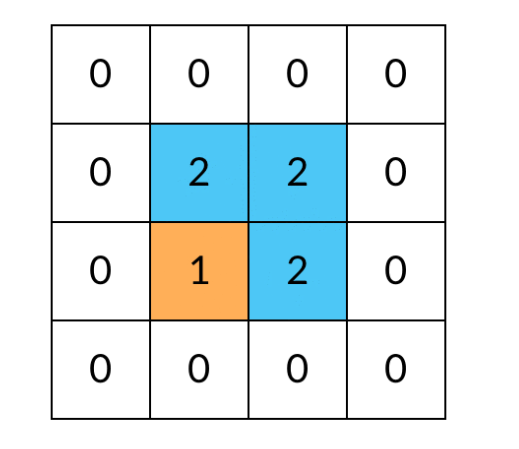
（5）这样，就得到了网格DFS遍历的框架代码。

java 复制代码

// 标记已遍历过的岛屿，不做重复遍历
void dfs(int[][] grid, int r, int c) {
    if (!(0 <= r && r < grid.length && 0 <= c && c < grid[0].length)) {
        return;
    }
    // 已遍历过（值为2）的岛屿在这里会直接返回，不会重复遍历
    if (grid[r][c] != 1) {
        return;
    }
    grid[r][c] = 2; // 将方格标记为"已遍历"
    dfs(grid, r - 1, c); 
    dfs(grid, r + 1, c);
    dfs(grid, r, c - 1);
    dfs(grid, r, c + 1);
}

（6）如何在DFS遍历时求岛屿的周长：求岛屿周长的方法很多，如果用DFS遍历来求的话，有一种很简单的思路，那就是岛屿的周长就是岛屿方格和非岛屿方格相邻的边的数量。这里的非岛屿方格既包括水域，也包括网格的边界，如下图所示。

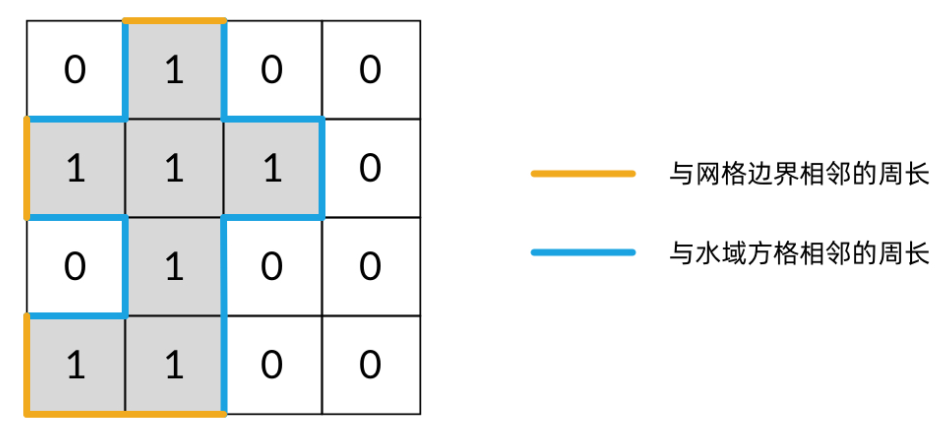
将这个相邻关系对应到DFS遍历中，就是：每当在DFS遍历中，从一个岛屿走向一个非岛屿方格，就将周长 + 1。代码如下所示。

java 复制代码

int dfs(int[][] grid, int r, int c) {
    // 从一个岛屿方格走向网格边界，周长加 1
    if (!(0 <= r && r < grid.length && 0 <= c && c < grid[0].length)) {
        return 1;
    }
    // 从一个岛屿方格走向水域方格，周长加 1
    if (grid[r][c] == 0) {
        return 1;
    }
    if (grid[r][c] != 1) {
        return 0;
    }
    grid[r][c] = 2;
    return dfs(grid, r - 1, c)
        + dfs(grid, r + 1, c)
        + dfs(grid, r, c - 1)
        + dfs(grid, r, c + 1);
}

附代码：

java 复制代码

class Solution {
    public int islandPerimeter(int[][] grid) {
        for(int r = 0;r < grid.length;r++){
            for(int c = 0;c < grid[0].length;c++){
                if(grid[r][c] == 1){
                    //题目限制只有一个岛屿，计算一个即可
                    return dfs(grid,r,c);
                }
            }
        }
        return 0;
    }
    int dfs(int[][] grid,int r,int c){
        //先污染后治理，只需要在开头判断是否合法，若不合法则直接返回
        //从一个岛屿方格走向网格边界，周长加1
        if(!(r >= 0 && r < grid.length && c >= 0 && c < grid[0].length)){
            return 1;
        }
        //从一个岛屿方格走向水域方格，周长加1
        if(grid[r][c] == 0){
            return 1;
        }
        //已经遍历过，直接返回，避免重复遍历
        if(grid[r][c] == 2){
            return 0;
        }
        //将本方格标记为已经遍历过
        grid[r][c] = 2;
        //探索相邻格子，并将四个方向的周长计算结果相加
        return dfs(grid,r - 1,c) + dfs(grid,r + 1,c) + dfs(grid,r,c - 1) + dfs(grid,r,c + 1);
    }
}