19🎈. 螺旋矩阵
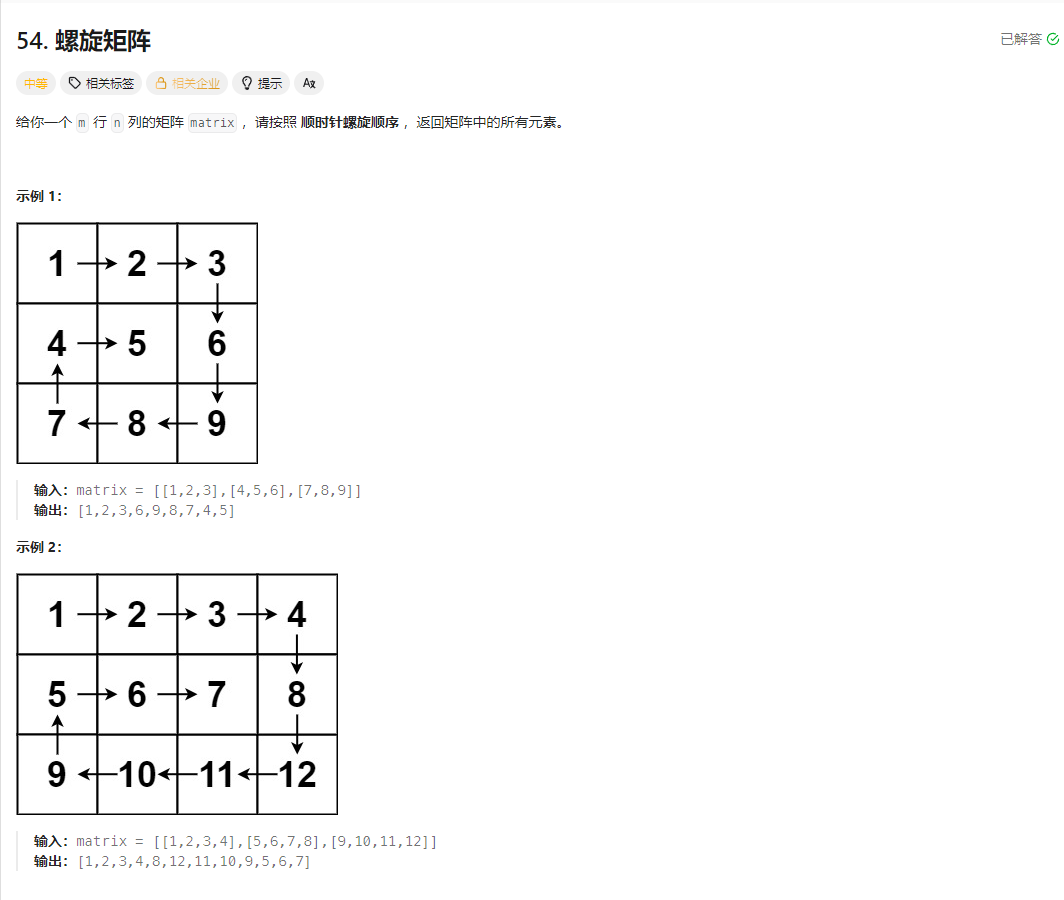

螺旋矩阵遍历算法解析
这个算法的核心思路是通过维护四个边界(上、下、左、右),按 "右→下→左→上" 的顺序逐层遍历矩阵,每遍历完一条边就收缩对应边界,直到边界交叉(遍历完成)。
一、核心变量定义
cpp
int u = 0; // 上边界(初始为第0行)
int d = matrix.size() - 1; // 下边界(初始为最后一行)
int l = 0; // 左边界(初始为第0列)
int r = matrix[0].size() - 1; // 右边界(初始为最后一列)
vector<int> ans; // 存储遍历结果二、遍历逻辑(循环体)
循环中按右→下→左→上的顺序遍历,每完成一条边就收缩边界,并检查是否已遍历完成(边界交叉)。
1. 第一步:从左到右遍历 "上边界" 行
cpp
for(int i = l; i <= r; ++i) ans.push_back(matrix[u][i]); // 向右遍历上边界行
if(++ u > d) break; // 上边界向下收缩,若上边界超过下边界,说明遍历完成- 遍历范围:左边界
l→ 右边界r,行固定为u(上边界)。 - 收缩边界:上边界
u加 1(后续不再遍历这一行)。 - 终止检查:如果新的上边界
u大于下边界d,说明所有行已遍历,直接退出循环。
2. 第二步:从上到下遍历 "右边界" 列
cpp
for(int i = u; i <= d; ++i) ans.push_back(matrix[i][r]); // 向下遍历右边界列
if(-- r < l) break; // 右边界向左收缩,若右边界小于左边界,遍历完成- 遍历范围:上边界
u→ 下边界d,列固定为r(右边界)。 - 收缩边界:右边界
r减 1(后续不再遍历这一列)。 - 终止检查:如果新的右边界
r小于左边界l,说明所有列已遍历,退出循环。
3. 第三步:从右到左遍历 "下边界" 行
cpp
for(int i = r; i >= l; --i) ans.push_back(matrix[d][i]); // 向左遍历下边界行
if(-- d < u) break; // 下边界向上收缩,若下边界小于上边界,遍历完成- 遍历范围:右边界
r→ 左边界l,行固定为d(下边界)。 - 收缩边界:下边界
d减 1(后续不再遍历这一行)。 - 终止检查:如果新的下边界
d小于上边界u,退出循环。
4. 第四步:从下到上遍历 "左边界" 列
cpp
for(int i = d; i >= u; --i) ans.push_back(matrix[i][l]); // 向上遍历左边界列
if(++ l > r) break; // 左边界向右收缩,若左边界大于右边界,遍历完成- 遍历范围:下边界
d→ 上边界u,列固定为l(左边界)。 - 收缩边界:左边界
l加 1(后续不再遍历这一列)。 - 终止检查:如果新的左边界
l大于右边界r,退出循环。
三、示例演示
以矩阵 [[1,2,3],[4,5,6],[7,8,9]] 为例:
| 步骤 | 遍历范围 | 结果 ans | 边界变化 |
|---|---|---|---|
| 1 | 上边界行(0 行):1→2→3 | [1,2,3] | u=1(上边界下移) |
| 2 | 右边界列(2 列):4→5→6?不,u=1→d=2 → 6→9 | [1,2,3,6,9] | r=1(右边界左移) |
| 3 | 下边界行(2 行):8→7 | [1,2,3,6,9,8,7] | d=1(下边界上移) |
| 4 | 左边界列(0 列):4 | [1,2,3,6,9,8,7,4] | l=1(左边界右移) |
| 循环再次执行 | 上边界行(1 行):5 | [1,2,3,6,9,8,7,4,5] | u=2 > d=1 → 退出 |
最终结果:[1,2,3,6,9,8,7,4,5],符合螺旋遍历顺序。
四、关键注意点
- 空矩阵处理 :开头判断
matrix.empty(),避免越界。 - 边界检查时机:每遍历完一条边就检查边界是否交叉,而非最后统一检查,避免重复遍历或越界。
- 遍历方向 :向左 / 向上遍历时,循环变量需从大到小(
i--/i>=)。
五、复杂度分析
- 时间复杂度:O (m×n),每个元素仅被遍历一次(m 行 n 列)。
- 空间复杂度:O (1)(除结果数组外,仅使用常数级变量)。
这个算法的优势是逻辑清晰、无冗余遍历,是螺旋矩阵遍历的最优解法之一。
20🎈. 旋转图像


矩阵旋转(顺时针 90 度)算法解析
这个算法的核心思路是分块原地旋转:将矩阵按 "层" 划分,每个元素与它旋转后对应的另外 3 个元素形成一组,通过临时变量完成 4 个元素的循环交换,最终实现整体顺时针旋转 90 度。
一、核心前提:旋转规律
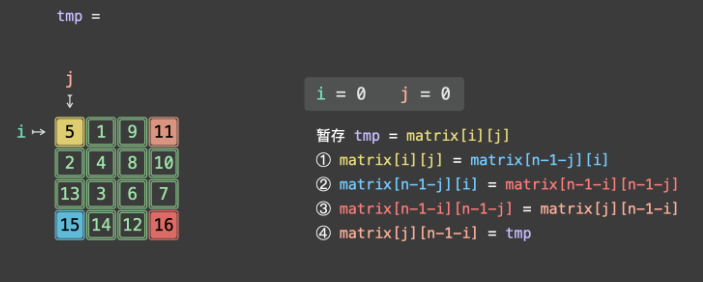
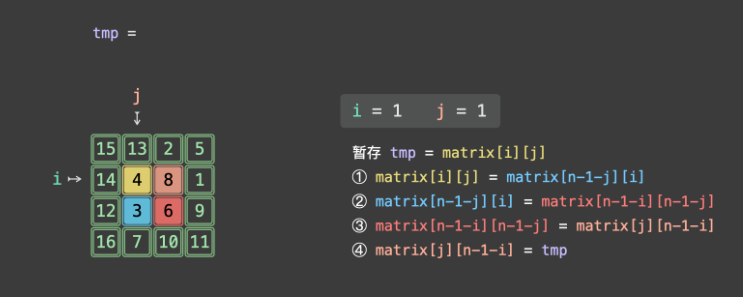
对于 n×n 的正方形矩阵,顺时针旋转 90 度后,原位置 (i, j) 的元素会移动到 (j, n-1-i),且 4 个位置形成一个循环:
cpp
原位置 A(i, j) → 位置 B(j, n-1-i) → 位置 C(n-1-i, n-1-j) → 位置 D(n-1-j, i) → 回到 A(i, j)举例(n=3):原位置 (0,0) → (0,2) → (2,2) → (2,0) → 回到 (0,0)。
二、变量与循环范围
cpp
int n = matrix.size(); // 矩阵边长(n×n)
// 外层循环:遍历"层",只需处理前 n/2 层(内层循环处理每层的元素)
for (int i = 0; i < n / 2; i++) {
// 内层循环:遍历每层需要交换的元素,范围是 (n+1)/2
for (int j = 0; j < (n + 1) / 2; j++) {
// ... 交换逻辑
}
}循环范围的关键解释:
- 外层循环
i < n/2:矩阵按 "环" 分层,比如 n=3 时只有 1 层(i=0),n=4 时有 2 层(i=0、1),只需处理前半层即可覆盖所有需要交换的元素。 - 内层循环
j < (n+1)/2:避免重复交换,比如:- n=3(奇数):
(3+1)/2=2,j=0、1(覆盖每层的 2 个元素,即可完成所有 4 元组交换); - n=4(偶数):
(4+1)/2=2(整数除法),j=0、1(覆盖每层的 2 个元素)。
- n=3(奇数):
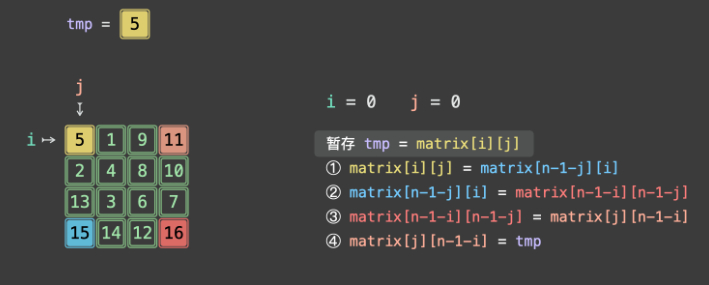
三、核心交换逻辑
cpp
// 保存原位置 A(i,j) 的值到临时变量
int tmp = matrix[i][j];
// D → A:把位置 D 的值放到 A
matrix[i][j] = matrix[n - 1 - j][i];
// C → D:把位置 C 的值放到 D
matrix[n - 1 - j][i] = matrix[n - 1 - i][n - 1 - j];
// B → C:把位置 B 的值放到 C
matrix[n - 1 - i][n - 1 - j] = matrix[j][n - 1 - i];
// 原A(tmp)→ B:把临时变量的值放到 B
matrix[j][n - 1 - i] = tmp;交换步骤拆解(以 4 元组 A→B→C→D→A 为例):
- 先保存
A的值(避免被覆盖); - 把
D放到A的位置; - 把
C放到D的位置; - 把
B放到C的位置; - 把最初保存的
A放到B的位置;最终完成 4 个元素的顺时针旋转。
四、示例演示(n=3,矩阵 [[1,2,3],[4,5,6],[7,8,9]])
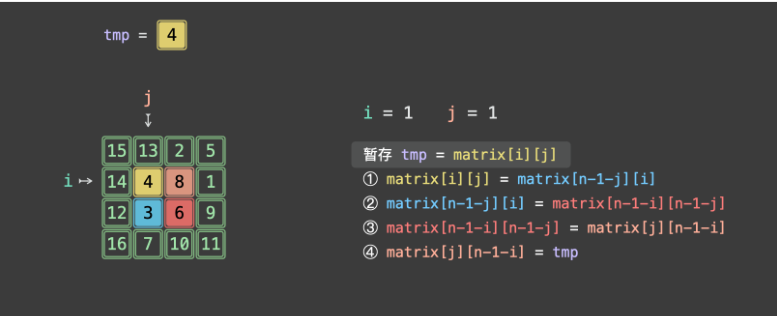
第一步:i=0(第一层),j=0
- 4 元组位置:A (0,0)=1、B (0,2)=3、C (2,2)=9、D (2,0)=7
- 交换过程:
- tmp = 1;
- matrix[0][0] = matrix[2][0] → (0,0)=7;
- matrix[2][0] = matrix[2][2] → (2,0)=9;
- matrix[2][2] = matrix[0][2] → (2,2)=3;
- matrix[0][2] = tmp → (0,2)=1;
- 矩阵变为:
[[7,2,1],[4,5,6],[9,8,3]]
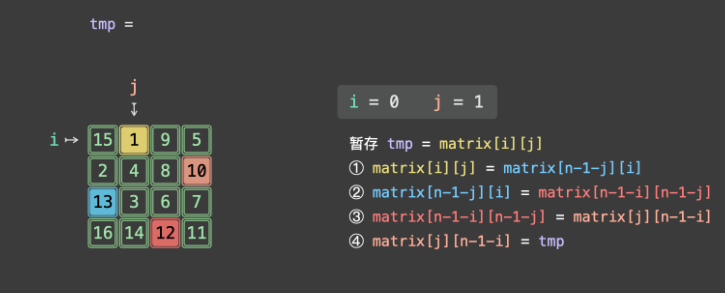
第二步:i=0,j=1
- 4 元组位置:A (0,1)=2、B (1,2)=6、C (2,1)=8、D (1,0)=4
- 交换过程:
- tmp = 2;
- matrix[0][1] = matrix[1][0] → (0,1)=4;
- matrix[1][0] = matrix[2][1] → (1,0)=8;
- matrix[2][1] = matrix[1][2] → (2,1)=6;
- matrix[1][2] = tmp → (1,2)=2;
- 矩阵最终变为:
[[7,4,1],[8,5,2],[9,6,3]](符合顺时针旋转 90 度的结果)。
五、复杂度分析
- 时间复杂度:O (n²),每个元素仅被交换一次(总共 n² 个元素)。
- 空间复杂度 :O (1),仅使用临时变量
tmp,原地旋转无额外空间开销。
六、关键注意点
- 仅适用于正方形矩阵 :代码中默认输入是
n×n矩阵,若为非正方形需额外处理(但题目通常要求正方形旋转); - 循环范围的准确性 :
n/2和(n+1)/2是避免重复交换的核心,若范围错误会导致元素被重复旋转或遗漏; - 4 元组位置的对应关系 :需牢记
(i,j) ↔ (n-1-j,i) ↔ (n-1-i,n-1-j) ↔ (j,n-1-i)的映射规律,这是交换的核心。









21🎈. 搜索二维矩阵 II

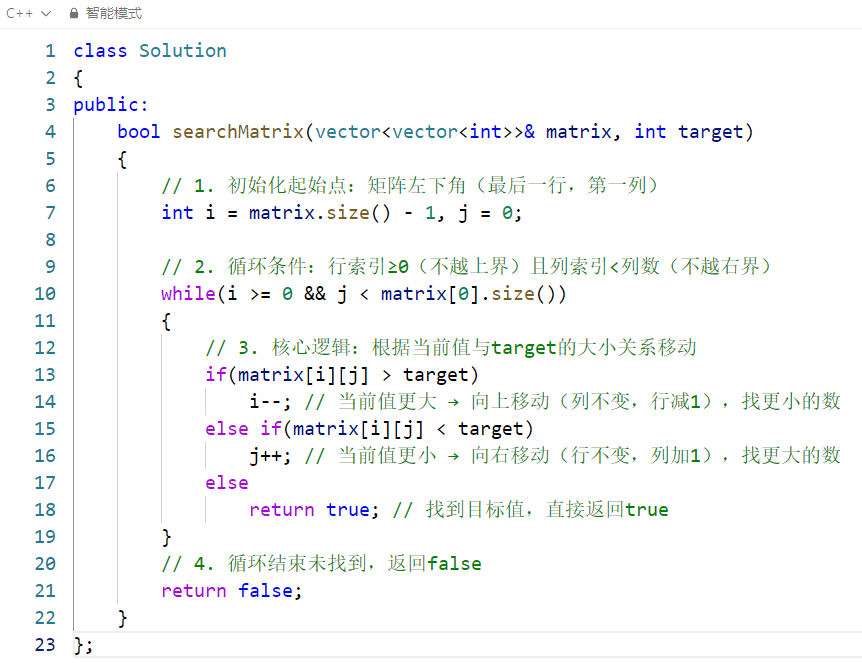
解题思路:
若使用暴力法遍历矩阵 matrix ,则时间复杂度为 O(NM) 。暴力法未利用矩阵 "从上到下递增、从左到右递增" 的特点,显然不是最优解法。
该算法利用矩阵的行递增、列递增特性 ,选择矩阵左下角 作为起始点,通过 "比较 - 移动" 的方式逐步缩小搜索范围,时间复杂度为O(m+n)(m 为行数,n 为列数),空间复杂度为**(O(1)**,是最优解法之一。
如下图所示,我们将矩阵逆时针旋转 45° ,并将其转化为图形式,发现其类似于 二叉搜索树 ,即对于每个元素,其左分支元素更小、右分支元素更大。因此,通过从 "根节点" 开始搜索,遇到比 target 大的元素就向左,反之向右,即可找到目标值 target 。
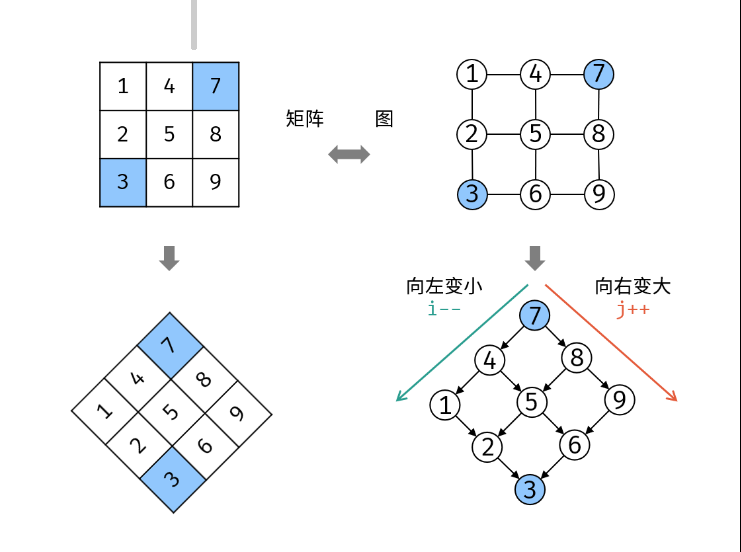






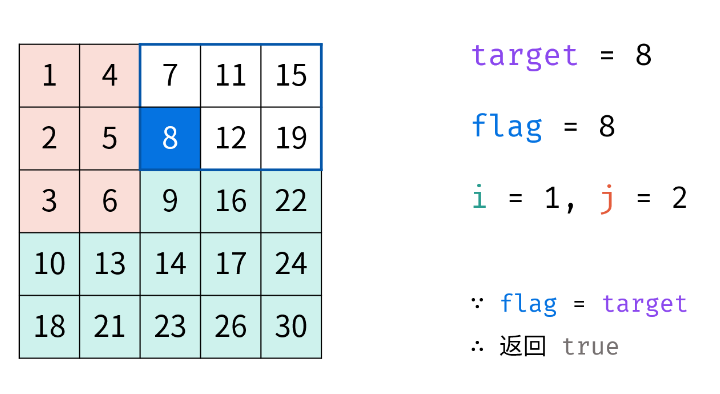
以左下角为起点的合理性:
| 情况 | 移动方向 | 逻辑依据 |
|---|---|---|
| 当前值 > target | 向上 | 列递增 → 当前列下方的数都比当前值大,不可能是 target,只能向上找更小的数 |
| 当前值 < target | 向右 | 行递增 → 当前行左侧的数都比当前值小,不可能是 target,只能向右找更大的数 |
| 当前值 == target | 返回 true | 找到目标 |
边界情况说明
- 矩阵只有一行:起始点为该行第一个元素,若target更大则向右移动,直到找到或越界;
- 矩阵只有一列:起始点为最后一行该列,若target更小则向上移动,直到找到或越界;
- target 小于矩阵最小值:向上移动直到 i=-1,返回 false;
- target 大于矩阵最大值:向右移动直到j = 列数 ,返回false。
复杂度分析:
时间复杂度O(M+N) :其中,N 和 M 分别为矩阵行数和列数,此算法最多循环 M+N 次。
空间复杂度 O(1) : i, j指针使用常数大小额外空间。
🔥链表
22🎈. 相交链表

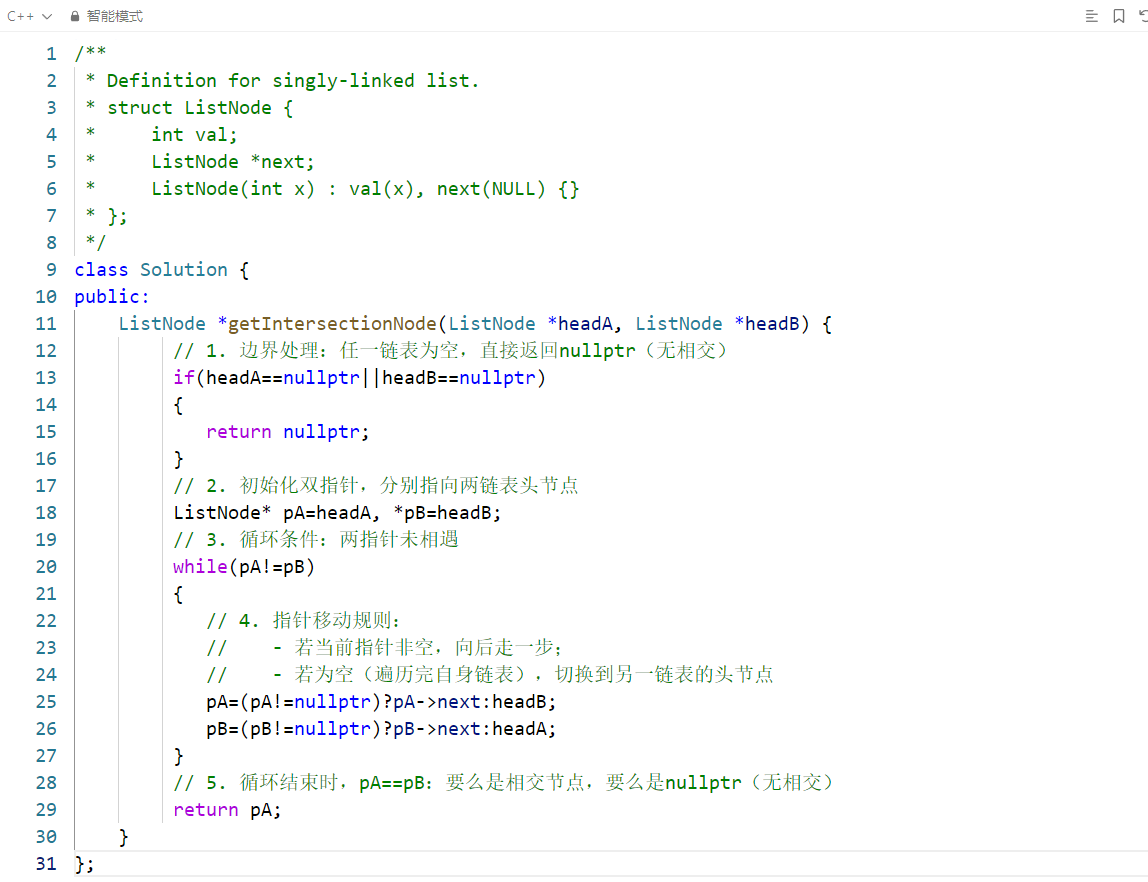
一、核心思路
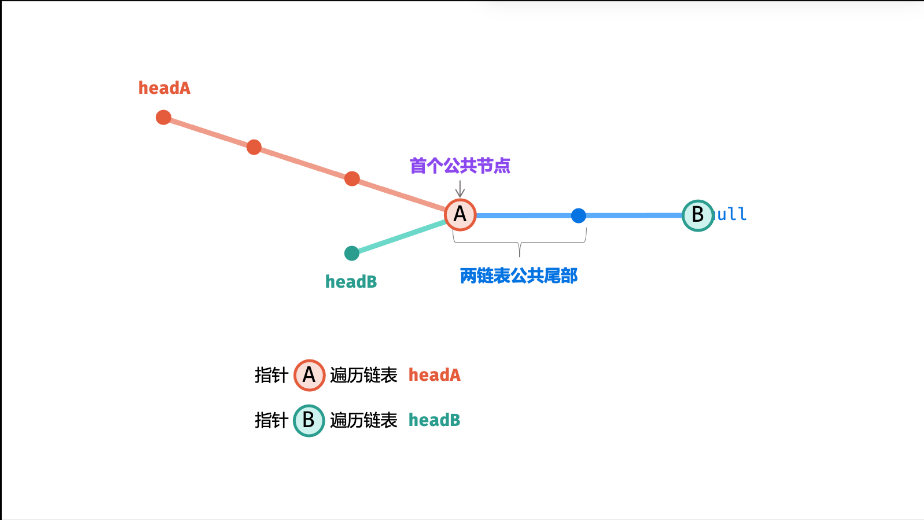
该算法利用双指针 "对齐长度差" 的思想,解决两个单链表的相交节点查找问题。核心逻辑是:让两个指针分别遍历两个链表,遍历完自身链表后切换到另一个链表的头节点继续遍历,最终两个指针会在相交节点相遇(或同时到达 nullptr,表示无相交)。时间复杂度 \(O(m+n)\)(\(m、n\) 为两链表长度),空间复杂度 \(O(1)\),是最优解法。
二、问题前提与关键特性
- 相交链表定义 :两个链表相交,指的是节点地址相同(而非值相同),相交后两个链表共享后续所有节点(形状像 "Y",而非 "X");
- 若两链表相交,设:
- 链表 A:
a个节点(不包含相交部分) +c个公共节点; - 链表 B:
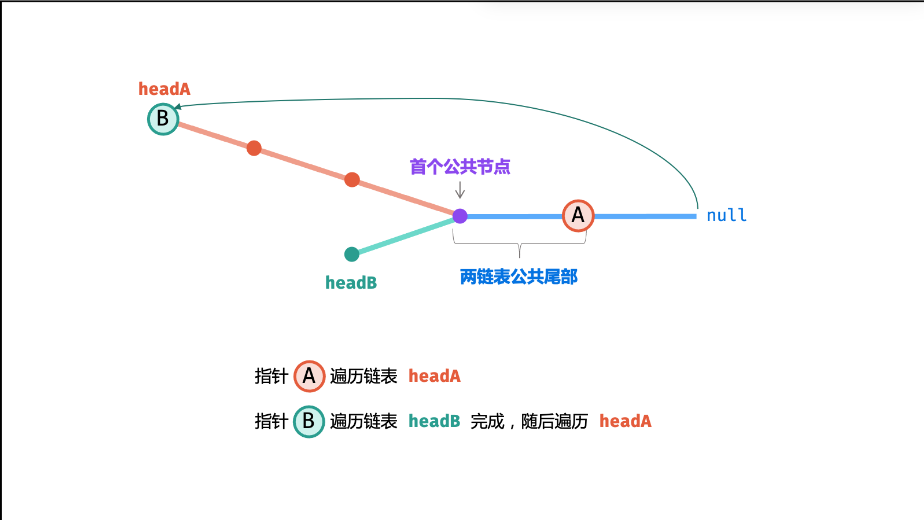
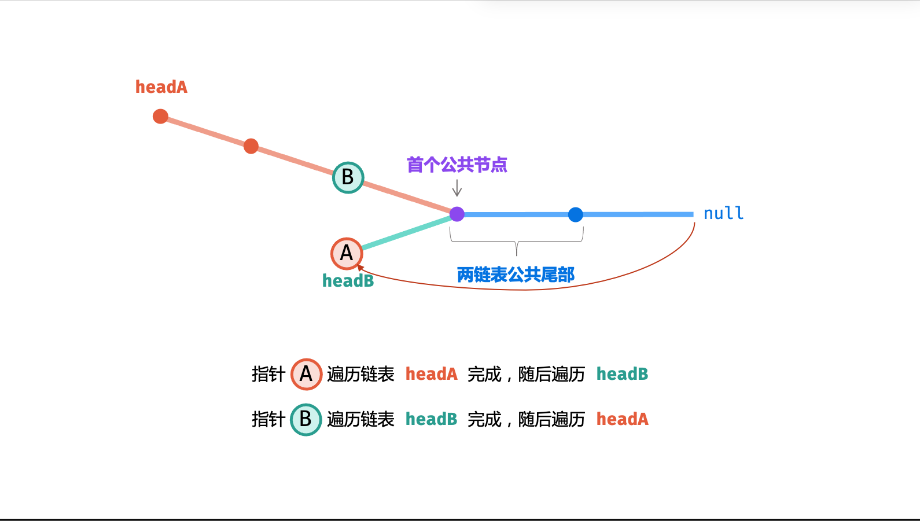
b个节点(不包含相交部分) +c个公共节点; - 则指针 A 遍历路径:a + c + b,指针 B 遍历路径:b + c + a → 路径长度相等,最终会在相交节点相遇。
- 链表 A:

四、核心逻辑推导
场景 1:两链表相交
假设链表 A:1 → 2 → 3 → 4(长度 4),链表 B:6 → 7 → 3 → 4(长度 4),相交节点为3。
- 指针 pA 遍历路径:
1 → 2 → 3 → 4 → 6 → 7 → 3 - 指针 pB 遍历路径:
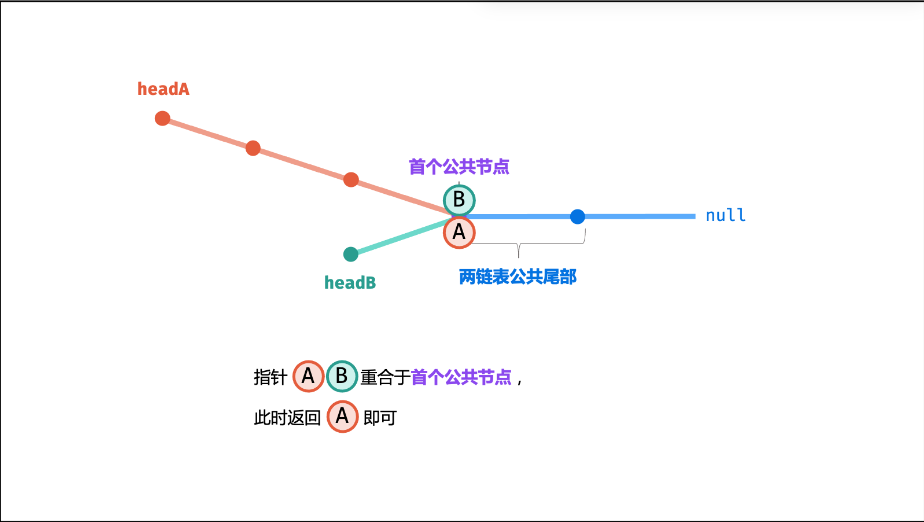
6 → 7 → 3 → 4 → 1 → 2 → 3 - 最终 pA 和 pB 在节点
3相遇,循环结束,返回3。
场景 2:两链表无相交
假设链表 A:1 → 2 → 3,链表 B:4 → 5。
- 指针 pA 遍历路径:
1 → 2 → 3 → nullptr → 4 → 5 → nullptr - 指针 pB 遍历路径:
4 → 5 → nullptr → 1 → 2 → 3 → nullptr - 最终 pA 和 pB 同时到达
nullptr,循环结束,返回nullptr。
场景 3:两链表长度差异大
假设链表 A:1 → 2 → 3 → 4 → 5(长度 5),链表 B:6 → 4 → 5(长度 3),相交节点为4。
- 指针 pA 遍历路径:
1 → 2 → 3 → 4 → 5 → 6 → 4(总长度 5+3=8) - 指针 pB 遍历路径:
6 → 4 → 5 → 1 → 2 → 3 → 4(总长度 3+5=8) - 最终在节点
4相遇,返回4。

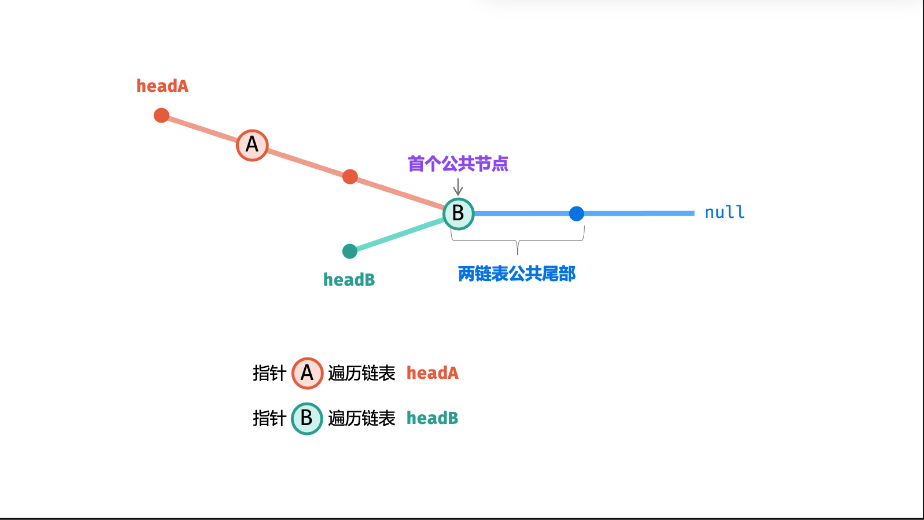
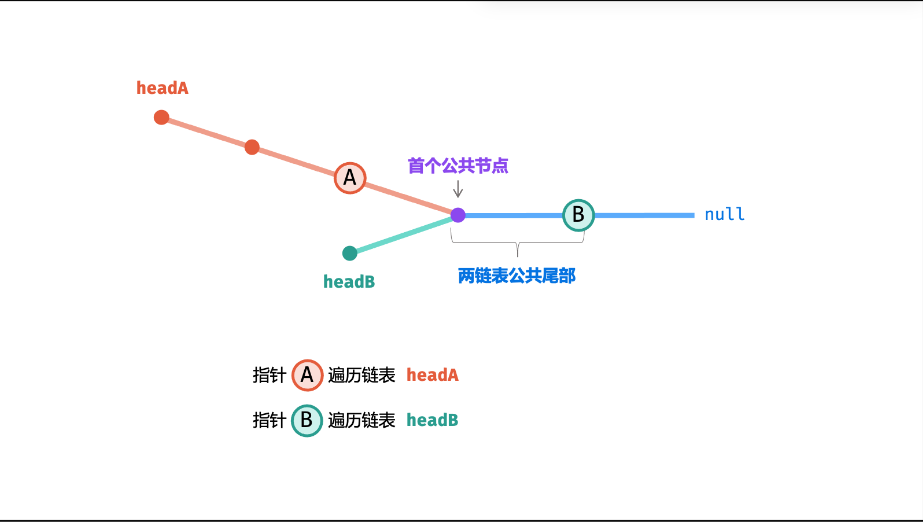

五、关键细节说明
-
为什么切换链表能对齐长度差? 假设链表 A 长度为
m,链表 B 长度为n:- 若
m > n:pB 先遍历完 B(n步),切换到 A 后,还需走m-n步才能和 pA "同步"; - 若
m < n:pA 先遍历完 A(m步),切换到 B 后,还需走n-m步才能和 pB "同步"; - 最终两指针遍历的总步数均为
m+n,必然在相交节点(或nullptr)相遇。
- 若
-
为什么循环条件是
pA != pB?- 若有相交:两指针最终会指向同一个相交节点,循环终止;
- 若无相交:两指针最终会同时指向
nullptr,循环终止(因为nullptr == nullptr)。
-
边界情况覆盖:
- 任一链表为空:直接返回
nullptr; - 两链表完全重合(头节点就是相交节点):第一次循环
pA==pB,直接返回头节点; - 相交节点为最后一个节点:指针遍历完自身链表后切换,最终在最后一个节点相遇。
- 任一链表为空:直接返回
六、对比其他解法的优势
| 解法 | 时间复杂度 | 空间复杂度 | 缺点 |
|---|---|---|---|
| 哈希表存储节点 | O(m+n) | O(m)或O(n) | 需要额外空间存储节点地址 |
| 先计算长度差再遍历 | O(m+n) | O(1) | 需两次遍历(计算长度 + 找交点) |
| 本解法(双指针切换) | O(m+n) | O(1) | 一次遍历完成,逻辑简洁 |
该解法的核心是用 "切换链表" 的方式隐式补偿长度差,无需额外计算长度,代码简洁且效率最优。
23🎈. 反转链表
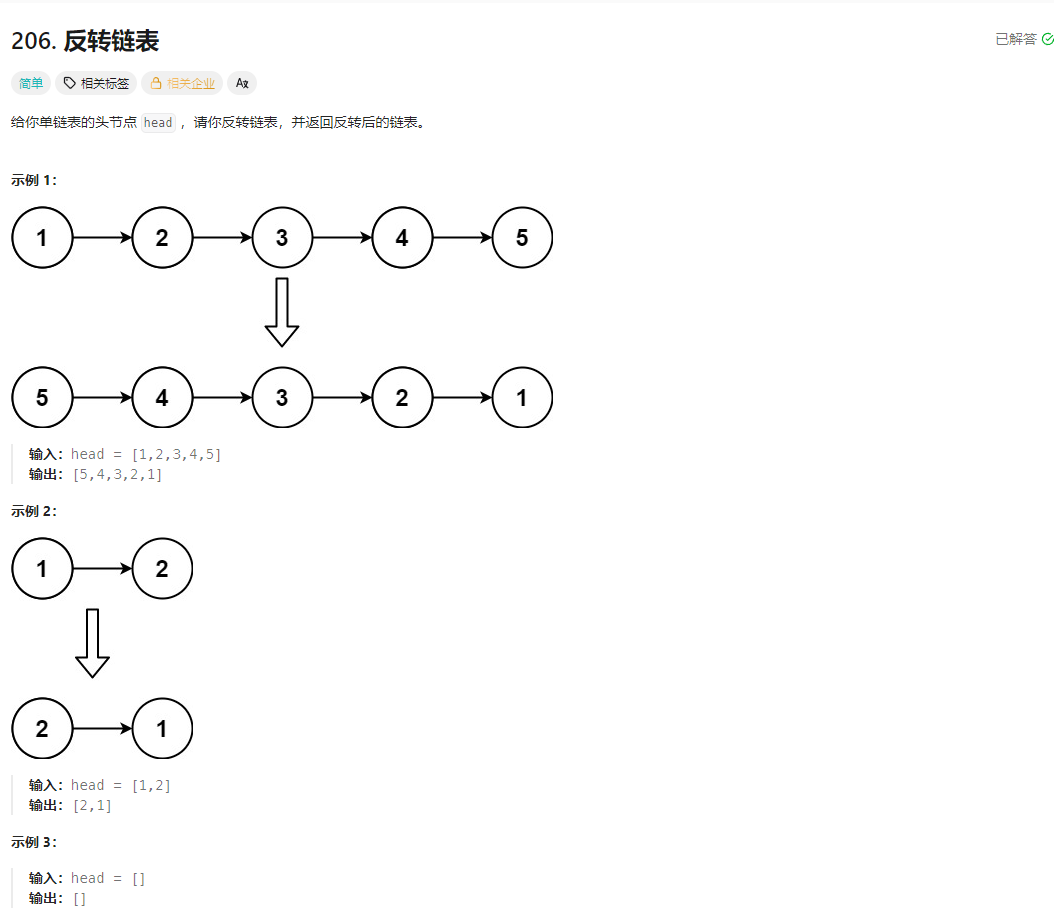
方法一:迭代(双指针)
考虑遍历链表,并在访问各节点时修改 next 引用指向
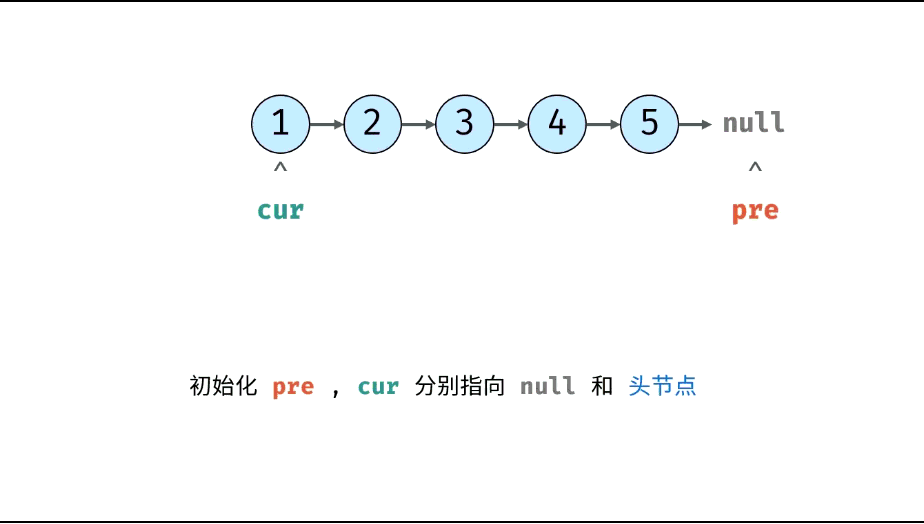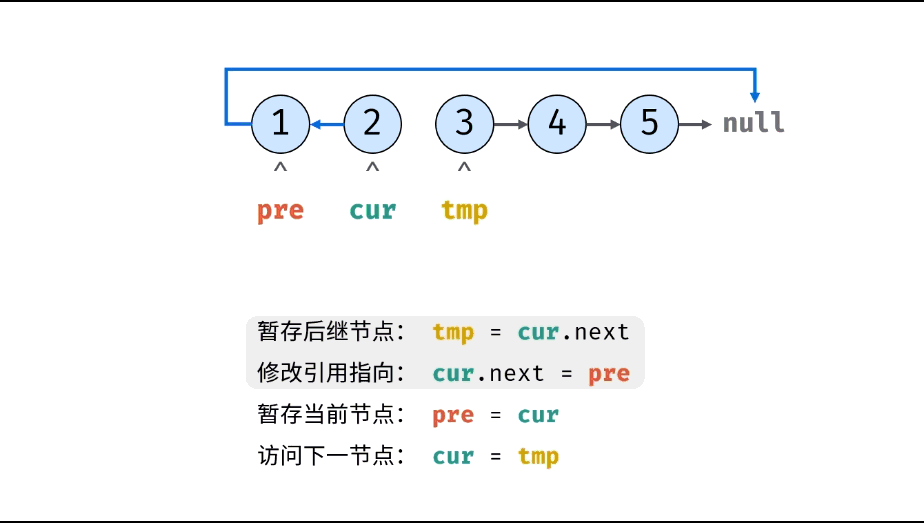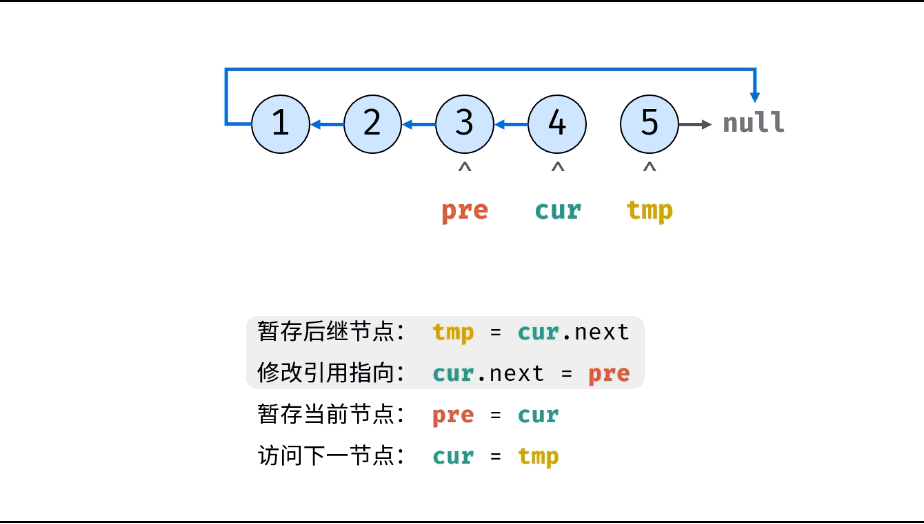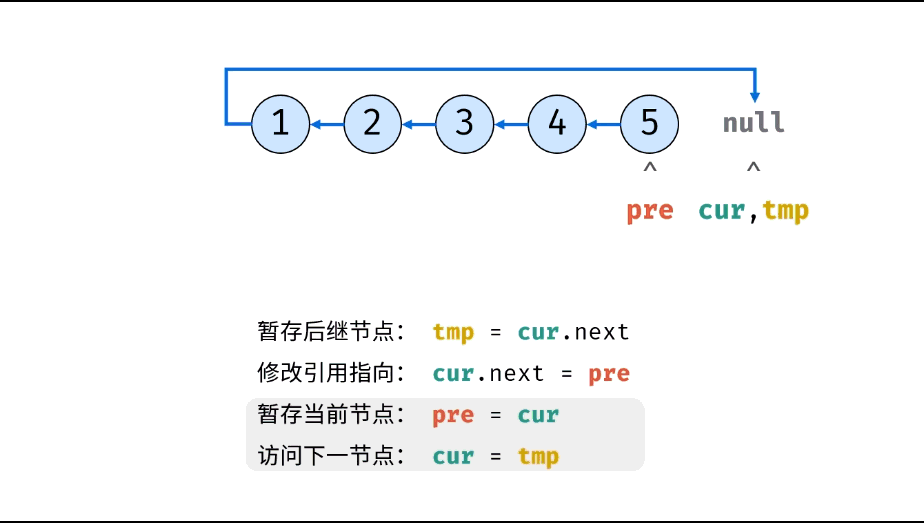
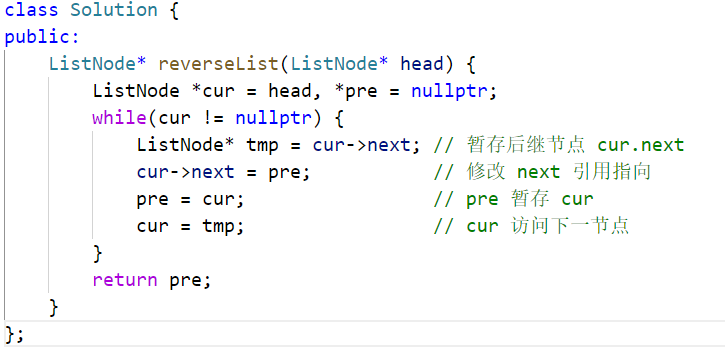
复杂度分析:
- 时间复杂度 O(N) : 遍历链表使用线性大小时间。
- 空间复杂度 O(1) : 变量
pre和cur使用常数大小额外空间。
方法二:递归
考虑使用递归法遍历链表,当越过尾节点后终止递归,在回溯时修改各节点的 next 引用指向。



一、核心思路
该算法采用递归 方式实现单链表反转,核心思想是:通过递归逐层深入到链表末尾(找到反转后的头节点),再从后往前逐层修改节点的 next 指针指向(让当前节点指向其前驱节点),最终完成整个链表的反转。时间复杂度 \(O(n)\)(n 为链表长度,每个节点递归一次),空间复杂度 \(O(n)\)(递归调用栈的深度)。
二、递归的核心逻辑
递归反转的关键是 **"归的过程" 修改指针 **:
- 递:不断递归到链表最后一个节点(该节点会成为反转后的头节点);
- 归:从最后一个节点开始,逐层将当前节点的
next指向其前驱节点,直到回到原链表头节点。
三、递归过程推演(示例链表:1→2→3→nullptr)
以链表 1→2→3→nullptr 为例,逐步拆解递归调用和指针修改过程:
步骤 1:初始调用
reverseList(head=1) → 调用 recur(cur=1, pre=nullptr)。
步骤 2:递的过程(逐层深入)
| 递归调用 | 执行逻辑 | 状态说明 |
|---|---|---|
recur(1, nullptr) |
cur≠null → 调用 recur(2, 1) |
准备处理节点 2 |
recur(2, 1) |
cur≠null → 调用 recur(3, 2) |
准备处理节点 3 |
recur(3, 2) |
cur≠null → 调用 recur(null, 3) |
准备处理节点 null |
recur(null, 3) |
cur=null → 返回 pre=3(反转后的头节点) | 递归终止,开始 "归" 的过程 |
步骤 3:归的过程(逐层修改指针)
| 递归返回 | 执行逻辑 | 链表状态变化 |
|---|---|---|
返回到 recur(3, 2) |
res=3 → 执行 3->next = 2 |
链表变为:1→2←3,3→null |
返回到 recur(2, 1) |
res=3 → 执行 2->next = 1 |
链表变为:1←2←3,3→null |
返回到 recur(1, nullptr) |
res=3 → 执行 1->next = nullptr |
链表变为:null←1←2←3(完成反转) |
步骤 4:最终返回
recur(1, nullptr) 返回 res=3 → reverseList 返回 3(反转后的头节点)。
四、关键细节说明
-
递归参数设计:
cur:当前需要处理的节点;pre:当前节点的前驱节点(反转后当前节点要指向的节点);- 初始时
cur=head,pre=nullptr(原头节点反转后是尾节点,指向 null)。
-
终止条件:
cur == nullptr时,说明已经遍历到链表末尾,此时pre就是反转后的头节点(原链表最后一个节点),直接返回。
-
res 变量的作用:
- 保存递归返回的 "反转链表头节点"(始终是原链表最后一个节点),在 "归" 的过程中逐层传递,最终作为整个递归的返回值。
-
指针修改的顺序:
- 先递归处理后继节点,再修改当前节点的
next指向 → 保证从后往前修改,避免提前断开链表(若先改指针,会丢失后继节点的引用)。
- 先递归处理后继节点,再修改当前节点的
五、边界情况覆盖
- 空链表 :
head=nullptr→ 调用recur(null, nullptr)→ 直接返回nullptr; - 单节点链表 :
head=1→ 调用recur(1, nullptr)→ 递归recur(null, 1)返回 1 → 执行1->next=null→ 返回 1(反转后还是自身); - 多节点链表:如上述示例,正常完成从后往前的指针反转。
六、递归与迭代的对比
| 解法 | 时间复杂度 | 空间复杂度 | 优势 | 缺点 |
|---|---|---|---|---|
| 递归 | \(O(n)\) | \(O(n)\) | 代码简洁,逻辑直观 | 递归栈可能溢出(链表过长时) |
| 迭代 | \(O(n)\) | \(O(1)\) | 空间效率更高,无栈溢出风险 | 代码稍繁琐,需手动维护指针 |
该递归解法的核心是利用递归栈天然的 "后进先出" 特性,实现从链表末尾到头部的指针反转,是链表反转的经典递归实现方式。
24🎈. 回文链表


【代码功能解析】
这段代码实现了判断单链表是否为回文链表 的功能。回文链表的定义是:链表节点的值从前往后和从后往前读取结果一致(如 1->2->2->1 是回文,1->2->3 不是)。
核心思路是:
- 找到链表的中间节点;
- 反转中间节点后的后半段链表;
- 对比前半段和反转后的后半段链表的节点值,全部相等则为回文。
【逐函数拆解】
cpp
ListNode* middleList(ListNode* head) {
ListNode *slow = head, *fast = head;
while (fast && fast->next) {
slow = slow->next; // 慢指针:每次走1步
fast = fast->next->next; // 快指针:每次走2步
}
return slow;
}- 原理 :快慢指针法(龟兔赛跑)
- 快指针速度是慢指针的 2 倍,当快指针走到链表末尾时,慢指针恰好走到中间位置。
- 链表长度为偶数 (如
1->2->3->4):慢指针停在第n/2 + 1个节点(示例中是3); - 链表长度为奇数 (如
1->2->3->4->5):慢指针停在正中间节点(示例中是3)。
- 作用:分割链表为前半段和后半段,后续只需反转后半段即可对比。
2. 辅助函数:reserveList(反转链表)
cpp
ListNode* reserveList(ListNode* head) {
ListNode* cur = head; // 当前遍历节点
ListNode* newNode = nullptr;// 反转后的新链表头
while (cur) {
ListNode* next = cur->next; // 保存当前节点的下一个节点(防止断链)
cur->next = newNode; // 当前节点指向新链表(头插法)
newNode = cur; // 更新新链表头为当前节点
cur = next; // 遍历下一个节点
}
return newNode;
}- 原理 :迭代法反转链表(头插法)
- 逐个遍历原链表节点,将每个节点 "摘下来" 插到新链表的头部,最终得到反转后的链表。
- 示例 :原链表
3->4→ 反转后4->3。
3. 主函数:isPalindrome(核心逻辑)
cpp
bool isPalindrome(ListNode* head) {
ListNode* mid = middleList(head); // 找中间节点
ListNode* rmid = reserveList(mid); // 反转后半段链表
while (head && rmid) { // 对比前半段和反转后的后半段
if (head->val != rmid->val) {
return false; // 有值不等,不是回文
}
head = head->next;
rmid = rmid->next;
}
return true; // 全部相等,是回文
}【示例推演】
示例 1:回文链表 1->2->2->1
- 找中间节点:慢指针走 2 步到
第二个2(mid = 2->1); - 反转后半段:
rmid = 1->2; - 对比:
head=1vsrmid=1→ 相等;head=2vsrmid=2→ 相等;- 循环结束,返回
true。
示例 2:非回文链表 1->2->3
- 找中间节点:慢指针走 2 步到
3(mid = 3); - 反转后半段:
rmid = 3; - 对比:
head=1vsrmid=3→ 不相等,返回false。
【复杂度分析】
- 时间复杂度 :O(n)
- 找中间节点:O (n/2);
- 反转后半段:O (n/2);
- 对比:O (n/2);
- 总复杂度为 O (n)。
- 空间复杂度 :O(1)
- 仅使用了常数个指针变量,没有额外开辟空间。
【注意事项】
- 边界情况:
- 空链表:直接返回
true; - 单节点链表:直接返回
true; - 双节点链表(如
1->1):返回true,1->2返回false。
- 空链表:直接返回
- 链表结构:代码中
reserveList会修改原链表的指针指向,但题目仅要求 "判断是否回文",未要求保留原链表结构,因此无需恢复。 - 拼写错误:代码中
reserveList应为reverseList(笔误,不影响逻辑,但实际开发中需修正)。