2025.12.18 论文阅读
一、文献阅读
题目信息
题目: 《Quantum Computers for Weather and Climate Prediction: The Good, the Bad, and the Noisy》
期刊: Bulletin of the American Meteorological Society
作者: F. Tennie and T. N. Palmer
发表时间: 2023
文章链接: https://doi.org/10.1175/BAMS-D-22-0031.1
摘要
本文旨在说明量子计算在天气和气候预测中的潜在应用。通过解释量子计算的基本原理,如量子比特、叠加态、纠缠,分析量子算法解决非线性微分方程的能力,并以简单非线性模型为例展示量子求解器的模拟结果。同时,文章讨论了量子计算在数据读取、噪声处理等方面的局限性,最终指出量子计算机短期内难以取代经典计算机,但可能在特定任务中发挥作用。
创新点
首次将量子非线性求解器应用于气象领域的简单非线性模型,提出量子噪声可能对非线性动力学积分有益的假设,并对比量子求解器与经典集合方法的结果差异。
理论基础
量子比特与纠缠
文章首先通过对比经典比特与量子比特,介绍了量子计算的基础。量子比特由复希尔伯特空间中的向量表示,能够处于叠加态。利用张量积,量子计算机可以将 n 个量子比特纠缠在一起,形成维度为 2 n 2^n 2n 的庞大状态空间 。这意味着一个拥有30个量子比特的量子计算机理论上可以编码具有10亿个变量的现代NWP模型状态 。
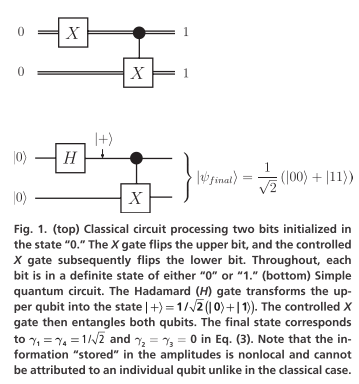
顶部展示了处理两个经典比特的电路,底部展示了包含Hadamard门和CNOT门的简单量子电路,生成了纠缠态 ∣ ψ f i n a l ⟩ = 1 2 ( ∣ 00 ⟩ + ∣ 11 ⟩ ) |\psi_{final}\rangle = \frac{1}{\sqrt{2}}(|00\rangle + |11\rangle) ∣ψfinal⟩=2 1(∣00⟩+∣11⟩)
量子求解器
为了克服薛定谔方程线性的限制以求解非线性气象方程,作者采用了基于多副本相互作用的算法:
作者首先将待求解变量编码为量子态。使用 N 个相同的系统副本。通过副本间的相互作用哈密顿量引入非线性项。单个副本的演化方程展现出非线性特性,这源于对其他副本自由度的平均。非线性项会导致均场误差,误差随副本数 N 的增加以 1/N 抑制,这意味着计算步数受限于 O(N) 。
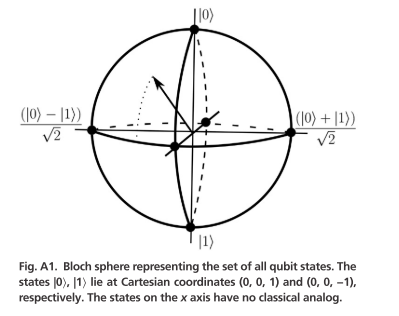
展示了单个量子比特的所有可能状态,其中 ∣ 0 ⟩ |0\rangle ∣0⟩ 和 ∣ 1 ⟩ |1\rangle ∣1⟩ 位于两极,赤道上的状态代表叠加态。
实验
作者在经典计算机上模拟了量子求解器的行为,对非线性模型进行了验证。
非线性方程积分与副本数验证
作者对模型 x ˙ ( t ) = x − α x 3 \dot{x}(t)=x-\alpha x^{3} x˙(t)=x−αx3进行了积分。使用 N=15 个副本运行量子求解器。
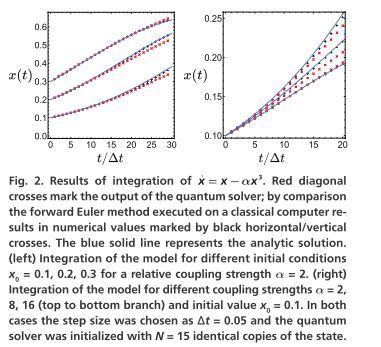
结果表明,误差随着积分步数积累,证明了均场误差的存在,且有效积分步数与副本数N成正比 。量子求解器的输出在约15个积分步长内与经典前向欧拉法及解析解高度一致 。
与经典系综预测的对比
作者比较了量子求解器与经典系综平均结果,针对方程 x ˙ = x − 8 x 3 \dot{x}=x-8x^{3} x˙=x−8x3。
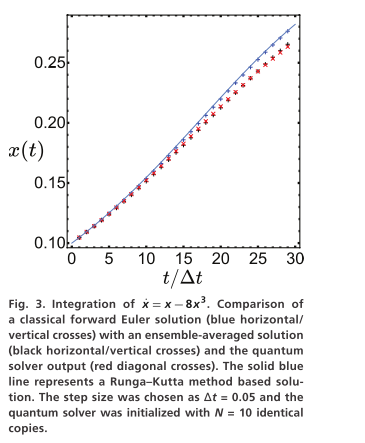
量子求解器的输出不仅跟随解析解,而且相比于单个经典解,它更接近于经典系综平均解。这表明量子算法在处理非线性系统时,可能自然地包含了某种形式的平滑或系综特性,这对于气象预报中的不确定性处理非常有价值。
结论
论文得出结论,量子计算即通过指数级大的希尔伯特空间高效编码庞大的模型状态 。虽然可以处理海量数据,但无法高效地读取所有结果,因为测量操作会将庞大的量子态坍缩为有限的经典比特。但量子计算中的噪声可能被转化为优势,用于模拟大气动力学中的随机过程 。
不足与展望
I/O 瓶颈是目前将量子计算应用于全尺度NWP的最大障碍。如果需要知道全球每个网格点的具体数值,量子计算机无法在合理时间内输出这些信息。
未来需要开发适用于气象非线性方程的高效量子算法;研究量子噪声与气象模型不确定性的关联性,设计容错量子硬件适配气象需求。鉴于目前的实际情况,未来应考虑量子-经典的路线。