掌握相关性分析：读懂数据间的“悄悄话”

在数据分析的江湖里，我们经常会听到老板或业务方抛出这样的问题：

• "现在的年轻人越晚睡，买护肤品是不是越疯狂？"
• "我们APP的各种优惠券，真的能提升用户的留存率吗？"
• "天气越热，这只股票是不是跌得越惨？"

面对这些问题，很多新人容易犯 "凭感觉" 的错误："我觉得应该有关系吧......"

数据分析不相信"我觉得"，只相信证据。 而寻找变量之间关系强弱的这个过程，就叫做相关分析。

今天，就带大家把相关分析的工具箱翻个底朝天，从基础到进阶，一次性讲透！

1. 什么是相关分析？

简单来说，相关分析就是判断两个或多个事物之间是否存在某种联系，以及这种联系有多紧密。

但请务必记住数据分析界的第一铁律：相关 \\neq 因果。

• 相关：公鸡叫了，天亮了。（它俩有关系，经常一起发生）
• 因果：因为公鸡叫了，所以天亮了。（这就错了，天亮是因为地球自转，不是因为鸡叫）

我们要做的，就是用数值（相关系数）来量化这种"一起发生"的程度。

2. 数据相关的"三剑客"

皮尔森相关系数 ，斯皮尔曼相关系数 和肯达尔相关系数 ，这是最常见的三种相关系数，它们处理的是数值型 或者有等级顺序的数据。

2.1. 皮尔森相关系数：精确测量的标准

皮尔森相关是最常用的相关性分析方法，适用于符合以下条件的数据：

• 连续数据（定距或定比尺度）
• 数据服从正态分布
• 变量间呈线性关系

这是最"挑剔"也是最常用的指标。它要求数据是连续数值 （定距/定比），并且最好服从正态分布 （钟形曲线）。它衡量的是线性关系（是不是一条直线）。

比如：身高和体重。一般来说，人越高，体重越重，这是一个比较标准的线性关系。

它的取值范围从 -1 到 1。接近 1 表示正相关 （同涨同跌），接近 -1 表示负相关 （此消彼长），0 表示没关系。

代码示例如下：

import numpy as np
import pandas as pd
from scipy import stats

# 模拟数据：运动时间(小时/周)与体重指数(BMI)
np.random.seed(42)

# 生成100个样本
n_samples = 100
exercise_time = np.random.normal(5, 2, n_samples)  # 平均每周运动5小时
# BMI与运动时间负相关（运动越多，BMI越低）
bmi = 25 - 0.5 * exercise_time + np.random.normal(0, 1.5, n_samples)

# 创建DataFrame
data = pd.DataFrame({'运动时间_小时每周': exercise_time, 'BMI': bmi})

# 计算皮尔森相关系数
pearson_corr, p_value = stats.pearsonr(data['运动时间_小时每周'], data['BMI'])
print(f"皮尔森相关系数: {pearson_corr:.3f}")
print(f"P值: {p_value:.5f}")

# 运行结果：
'''
皮尔森相关系数: -0.614
P值: 0.00000
'''

图形展示的效果如下：

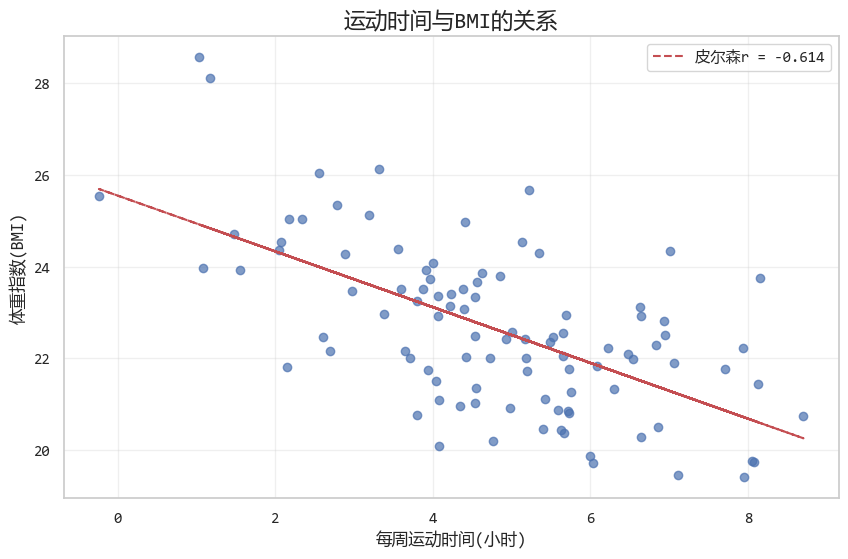
2.2. 斯皮尔曼相关系数：打破正态分布的限制

如果数据不服从正态分布 ，或者有极端值 （比如马云的财富混进了我们的收入数据中），皮尔森相关系数就不准了。

这时候用斯皮尔曼相关系数。它看重的是排名（Rank），而不是具体数值。

比如语文成绩排名和数学成绩排名，我们不关心具体考了多少分，只关心你的位次。

代码示例如下：

# 模拟数据：社交媒体表现
np.random.seed(42)

# 生成非正态分布的数据
followers = np.random.exponential(5000, 50)  # 指数分布
likes = 0.1 * followers**1.2 + np.random.normal(0, 1000, 50)  # 非线性关系

# 创建DataFrame
social_data = pd.DataFrame({"粉丝数": followers, "平均点赞数": likes})

# 计算斯皮尔曼相关系数
spearman_corr, spearman_p = stats.spearmanr(
    social_data["粉丝数"], social_data["平均点赞数"]
)
print(f"斯皮尔曼相关系数: {spearman_corr:.3f}")
print(f"P值: {spearman_p:.5f}")

# 运行结果：
'''
斯皮尔曼相关系数: 0.857
P值: 0.00000
'''

图形化结果如下：

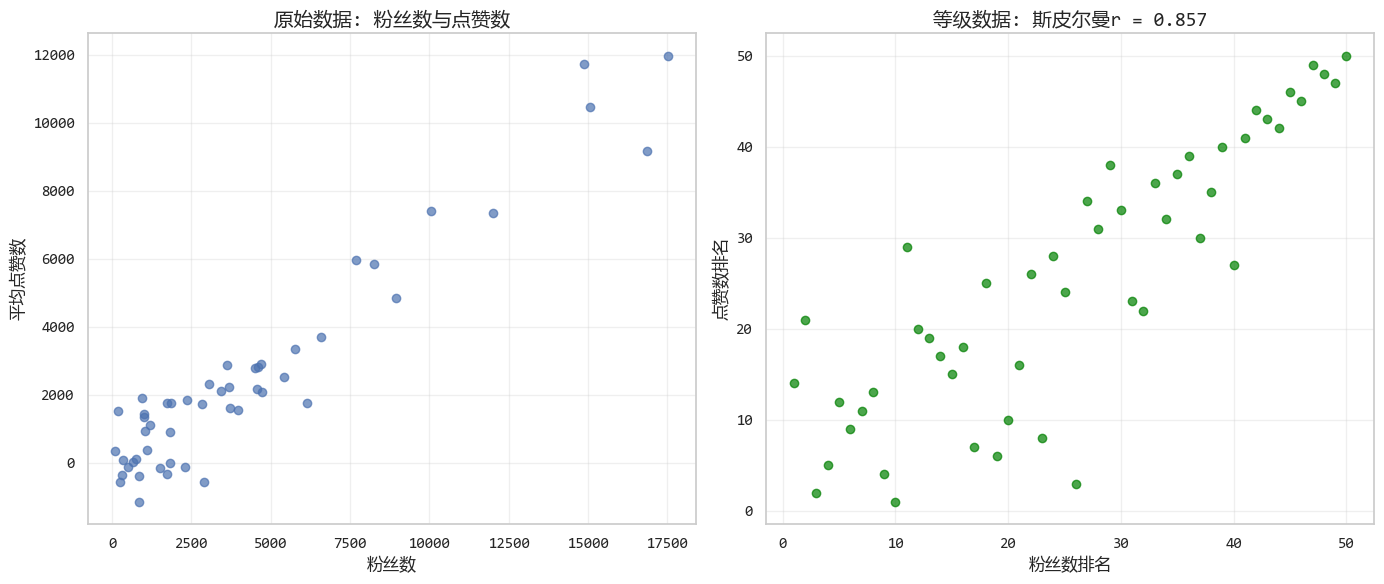
2.3. 肯达尔相关系数：小样本和有序数据的首选

肯达尔相关 也适用于等级数据，与斯皮尔曼相关不同，它更关注"和谐对"与"不和谐对"。

通常用于样本量较小，或者数据有很多并列排名的情况。

比如：两位面试官给5个候选人打分。我们要看这两位面试官的审美标准是否一致。

代码示例：

# 模拟数据：电影评分与票房
np.random.seed(42)

# 生成有序数据（电影评分和票房排名）
movie_data = pd.DataFrame(
    {
        "电影名称": [f"电影{i}" for i in range(1, 21)],
        "评分等级": np.random.choice(
            [1, 2, 3, 4, 5], 20, p=[0.1, 0.2, 0.3, 0.3, 0.1]
        ),  # 1-5星
        "票房排名": np.arange(1, 21),  # 票房排名
    }
)

# 添加一些相关性：评分越高，票房排名越好（数字越小）
for i in range(len(movie_data)):
    if movie_data.loc[i, "评分等级"] >= 4:
        movie_data.loc[i, "票房排名"] = max(
            1, movie_data.loc[i, "票房排名"] - np.random.randint(3, 8)
        )
    elif movie_data.loc[i, "评分等级"] <= 2:
        movie_data.loc[i, "票房排名"] = min(
            20, movie_data.loc[i, "票房排名"] + np.random.randint(3, 8)
        )

# 计算肯德尔相关系数
kendall_corr, kendall_p = stats.kendalltau(
    movie_data["评分等级"], movie_data["票房排名"]
)
print(f"肯德尔相关系数: {kendall_corr:.3f}")
print(f"P值: {kendall_p:.5f}")

# 运行结果：
'''
肯德尔相关系数: -0.503
P值: 0.00460
'''

图形化结果如下：

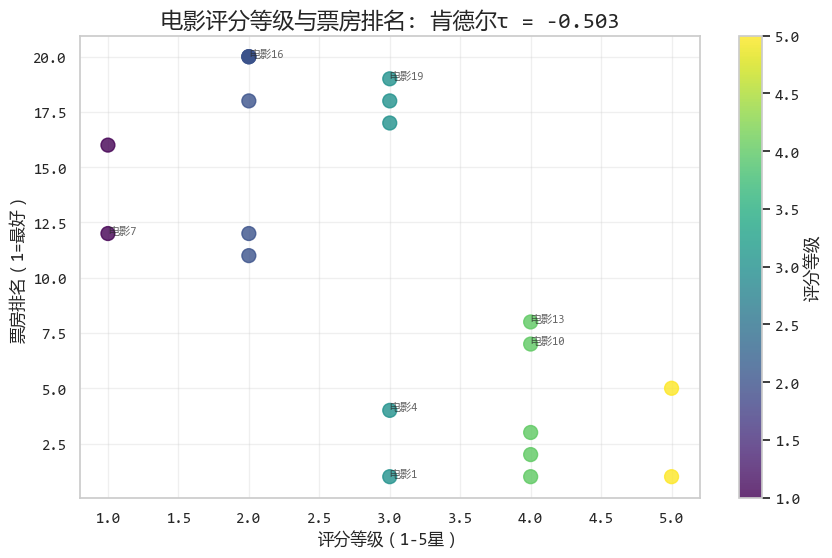
3. 偏相关分析：谁是"第三者"？

有时候，两个变量看起来关系很好，其实是因为有"第三者"在捣乱。

偏相关分析 允许我们在控制其他变量的情况下，分析两个变量之间的 "纯" 相关性。

比如一个生活中的案例："冰淇淋销量" 和 "溺水事故数量" 。

数据统计发现，冰淇淋卖得越好的日子，溺水的人越多（相关系数很高）。难道吃冰淇淋会导致溺水？

当然不是！背后的控制变量（第三者）是气温。气温高 -> 买冰淇淋多 & 游泳的人多 -> 溺水概率大。

想要正确分析，必须剔除控制变量（气温）的影响后，再看另外两个变量（冰淇淋和溺水）是否还相关。

下面的示例中，我们先排除收入影响后，分析教育水平与消费水平的关系。

# 使用pingouin库进行偏相关分析（需要安装：pip install pingouin）
import pingouin as pg

# 模拟数据：教育水平、收入和消费水平
np.random.seed(42)
n = 100

# 教育水平（1-5，5为最高）
education = np.random.choice([1, 2, 3, 4, 5], n, p=[0.1, 0.2, 0.3, 0.3, 0.1])

# 收入与教育水平正相关
income = 30000 + 15000 * education + np.random.normal(0, 5000, n)

# 消费水平与收入和教育水平都相关
consumption = 1000 + 0.3 * income + 200 * education + np.random.normal(0, 500, n)

# 创建DataFrame
socioeconomic_data = pd.DataFrame(
    {"教育水平": education, "收入_元每月": income, "消费水平": consumption}
)

print("=== 简单相关分析 ===")
simple_corr, simple_p = stats.pearsonr(
    socioeconomic_data["教育水平"], socioeconomic_data["消费水平"]
)
print(f"教育水平与消费水平的简单相关系数: {simple_corr:.3f}")

print("\n=== 偏相关分析（控制收入）===")
# 使用pingouin进行偏相关分析
partial_corr = pg.partial_corr(
    data=socioeconomic_data, x="教育水平", y="消费水平", covar="收入_元每月"
)
print(partial_corr.round(3))

# 运行结果：
'''
=== 简单相关分析 ===
教育水平与消费水平的简单相关系数: 0.965

=== 偏相关分析（控制收入）===
        n   r    	CI95%       	p-val
pearson	100	0.129	[-0.07, 0.32]	0.204
'''

图形化结果如下：

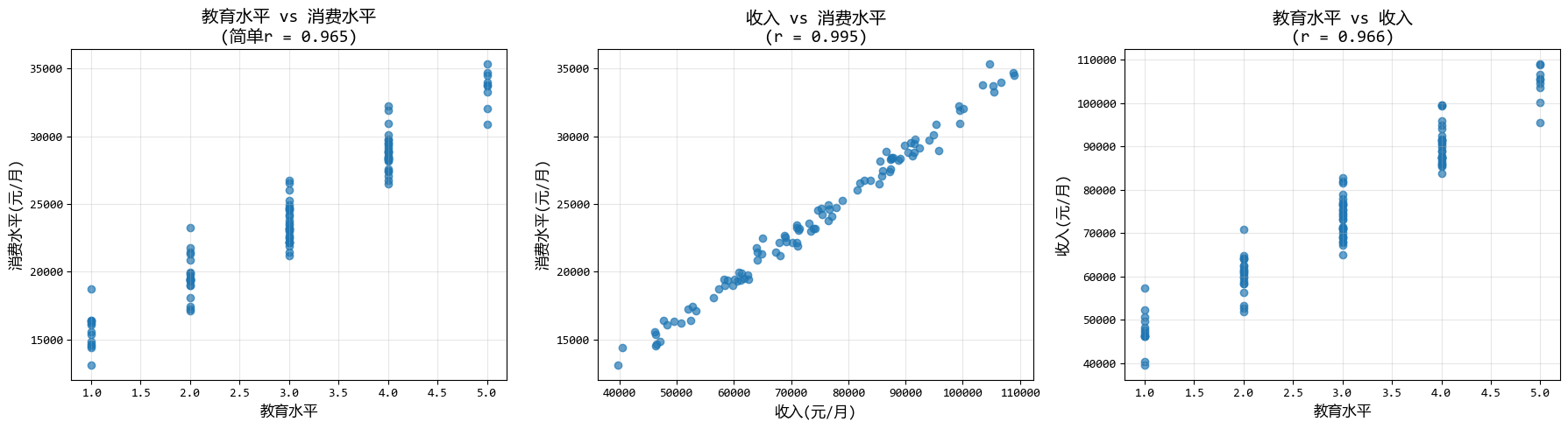
4. 距离相关分析：多变量关系的度量

距离相关分析 可以衡量两组变量（每个变量组包含多个指标）之间的相关性，是多变量分析的有力工具。

比如压力与工作效率（耶克斯-多德森定律）的关系。

压力太小，人会懒散（效率低）；压力太大，人会崩溃（效率低）；只有适度的压力，效率最高。

这是一个 U型（非线性） 关系。这时候用Pearson去算，结果可能是0（因为它找不到直线），但其实它们关系很紧密。

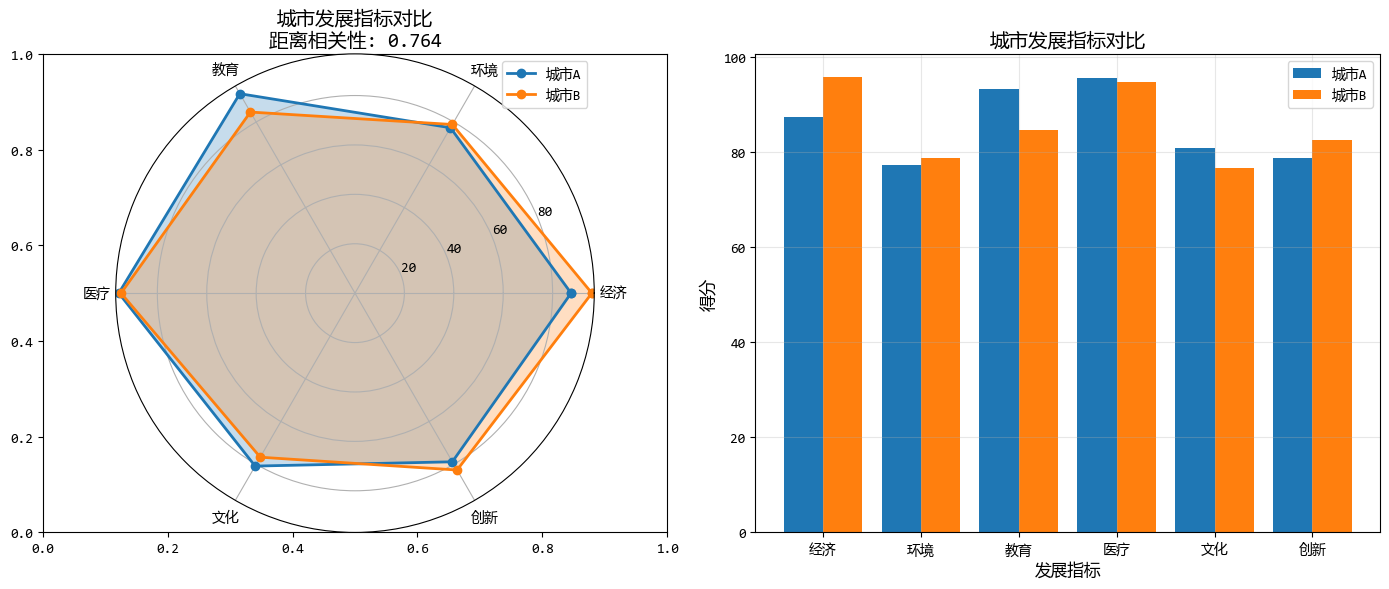
下面的示例，比较两个城市的综合发展水平（经济、环境、社会等多维度指标）。

from scipy.spatial.distance import pdist, squareform

# 模拟数据：两个城市的多维指标
np.random.seed(42)

# 城市A和城市B的6个发展指标（经济、环境、教育、医疗、文化、创新）
indicators = ["经济", "环境", "教育", "医疗", "文化", "创新"]
city_a = np.array([85, 78, 90, 88, 82, 80]) + np.random.normal(0, 5, 6)
city_b = np.array([88, 75, 87, 92, 79, 85]) + np.random.normal(0, 5, 6)

# 创建多个城市的比较数据
cities_data = pd.DataFrame(
    {
        "城市A": city_a,
        "城市B": city_b,
        "城市C": np.array([70, 85, 75, 80, 90, 72]) + np.random.normal(0, 5, 6),
        "城市D": np.array([92, 70, 85, 87, 76, 91]) + np.random.normal(0, 5, 6),
        "城市E": np.array([78, 88, 80, 85, 87, 78]) + np.random.normal(0, 5, 6),
    },
    index=indicators,
)

print("各城市发展指标数据：")
print(cities_data.round(2))


# 计算距离相关性（自定义简化版）
def distance_correlation(x, y):
    """计算距离相关性"""

    # 计算距离矩阵
    def dist_matrix(v):
        v = np.array(v)
        n = len(v)
        a = np.zeros((n, n))
        for i in range(n):
            for j in range(n):
                a[i, j] = abs(v[i] - v[j])
        return a

    A = dist_matrix(x)
    B = dist_matrix(y)

    # 双中心化
    def double_centering(D):
        n = len(D)
        row_means = D.mean(axis=1)
        col_means = D.mean(axis=0)
        grand_mean = D.mean()

        C = np.zeros((n, n))
        for i in range(n):
            for j in range(n):
                C[i, j] = D[i, j] - row_means[i] - col_means[j] + grand_mean
        return C

    A_centered = double_centering(A)
    B_centered = double_centering(B)

    # 计算距离协方差和距离方差
    dCov_XY = np.sqrt((A_centered * B_centered).sum() / (len(x) ** 2))
    dVar_X = np.sqrt((A_centered * A_centered).sum() / (len(x) ** 2))
    dVar_Y = np.sqrt((B_centered * B_centered).sum() / (len(x) ** 2))

    # 计算距离相关性
    dCor = dCov_XY / np.sqrt(dVar_X * dVar_Y)

    return dCor


# 比较城市A和城市B的距离相关性
city_a_scores = cities_data["城市A"].values
city_b_scores = cities_data["城市B"].values

dcor = distance_correlation(city_a_scores, city_b_scores)
print(f"\n城市A与城市B的距离相关性: {dcor:.3f}")

# 运行结果：
'''
各城市发展指标数据：
      城市A  城市B  城市C  城市D   城市E
经济  87.48  95.90  71.21  87.46  75.28
环境  77.31  78.84  75.43  62.94  88.55
教育  93.24  84.65  66.38  92.33  74.25
医疗  95.62  94.71  77.19  85.87  86.88
文化  80.83  76.68  84.94  76.34  84.00
创新  78.83  82.67  73.57  83.88  76.54

城市A与城市B的距离相关性: 0.764
'''

图形化的结果如下：

5. 相关性卡方检验：分类变量的关联分析

如果我们分析的数据不是数字，而是类别（定类数据/低测度数据）呢？

当两个变量都是分类变量（定类数据）时，我们可以使用卡方检验来分析它们之间是否存在关联。

比如性别（男/女） 与 爱喝的饮料（奶茶/咖啡） 是否相关？

这里没有大小之分，只有类别。我们可以使用卡方检验来判断两个分类变量是否独立。

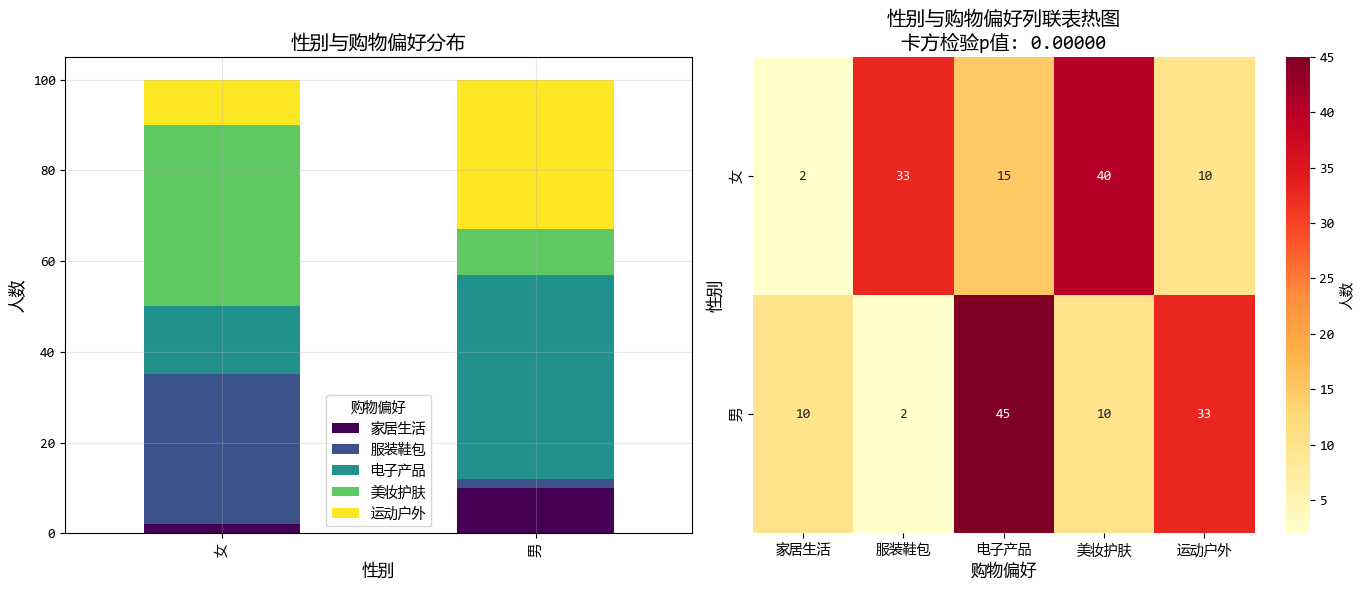
下面的示例，我们尝试分析性别与购物偏好类别之间的关系。

# 模拟数据：性别与购物偏好
np.random.seed(42)

# 创建列联表
data = pd.DataFrame(
    {
        "性别": np.random.choice(["男", "女"], 200),
        "购物偏好": np.random.choice(
            ["电子产品", "服装鞋包", "美妆护肤", "运动户外", "家居生活"], 200
        ),
    }
)

# 根据性别调整偏好概率（创建一些关联）
for i in range(len(data)):
    if data.loc[i, "性别"] == "男":
        # 男性更可能偏好电子产品和运动户外
        if np.random.random() < 0.3:
            data.loc[i, "购物偏好"] = "电子产品"
        elif np.random.random() < 0.5:
            data.loc[i, "购物偏好"] = "运动户外"
    else:
        # 女性更可能偏好美妆护肤和服装鞋包
        if np.random.random() < 0.3:
            data.loc[i, "购物偏好"] = "美妆护肤"
        elif np.random.random() < 0.4:
            data.loc[i, "购物偏好"] = "服装鞋包"

# 创建列联表
contingency_table = pd.crosstab(data["性别"], data["购物偏好"])
print("性别与购物偏好的列联表：")
print(contingency_table)

# 执行卡方检验
chi2, p, dof, expected = stats.chi2_contingency(contingency_table)
print(f"\n卡方检验结果：")
print(f"卡方值: {chi2:.3f}")
print(f"P值: {p:.5f}")
print(f"自由度: {dof}")
print(f"\n期望频数表：")
print(
    pd.DataFrame(
        expected, index=contingency_table.index, columns=contingency_table.columns
    ).round(2)
)


# 计算Cramer's V（衡量分类变量关联强度）
def cramers_v(contingency_table):
    """计算Cramer's V系数"""
    chi2 = stats.chi2_contingency(contingency_table)[0]
    n = contingency_table.sum().sum()
    min_dim = min(contingency_table.shape) - 1

    v = np.sqrt(chi2 / (n * min_dim))
    return v


cramers_v_value = cramers_v(contingency_table)
print(f"\nCramer's V系数: {cramers_v_value:.3f}")
print("解读：0.1-0.3弱相关，0.3-0.5中等相关，>0.5强相关")

# 运行结果：
'''
性别与购物偏好的列联表：
购物偏好  家居生活  服装鞋包  电子产品  美妆护肤  运动户外
性别
女        2    33    15    40    10
男       10     2    45    10    33

卡方检验结果：
卡方值: 78.093
P值: 0.00000
自由度: 4

期望频数表：
购物偏好  家居生活  服装鞋包  电子产品  美妆护肤  运动户外
性别
女      6.0  17.5  30.0  25.0  21.5
男      6.0  17.5  30.0  25.0  21.5

Cramer's V系数: 0.625
解读：0.1-0.3弱相关，0.3-0.5中等相关，>0.5强相关
'''

图形化的结果如下：

6. 总结

数据分析师在面对变量关系时，要根据数据的 "长相" 来选工具：

方法	适用数据类型	特点
皮尔森相关	连续、正态分布、线性关系	最常用，对异常值敏感
斯皮尔曼相关	连续但不正态，或有序数据	稳健，适用于单调关系
肯德尔相关	有序数据，小样本	适合等级数据，解释直观
偏相关	需控制其他变量影响	揭示变量间的直接关系
距离相关	多变量组间关系	衡量多维度综合关联
卡方检验	分类变量	检验类别间关联性

我们在分析数据相关性的时候，不要急于得出数据之间是否相关的结论。

先看看下面的注意事项是否有违背！

1. 相关性不等于因果性：即使两个变量高度相关，也不能断定一个导致另一个
2. 警惕第三变量问题：可能两个变量都受到第三个未测量变量的影响
3. 注意异常值的影响：异常值可能夸大或掩盖真实的相关性
4. 检查线性假设：皮尔森相关要求线性关系，非线性关系需要其他方法
5. 样本大小的重要性：小样本的相关性可能不稳定