
🔥个人主页:Cx330🌸
❄️个人专栏:《C语言》《LeetCode刷题集》《数据结构-初阶》《C++知识分享》
《优选算法指南-必刷经典100题》《Linux操作系统》:从入门到入魔
🌟心向往之行必能至
🎥Cx330🌸的简介:

目录
前言:
聚焦算法题实战,系统讲解三大核心板块:"精准定位最优解 "------优选算法,"简化逻辑表达,系统性探索与剪枝优化 "------递归与回溯,"以局部最优换全局高效 "------贪心算法,讲解思路与代码实现,帮助大家快速提升代码能力
01.第N个泰波拉契数
题目链接:
题目描述:
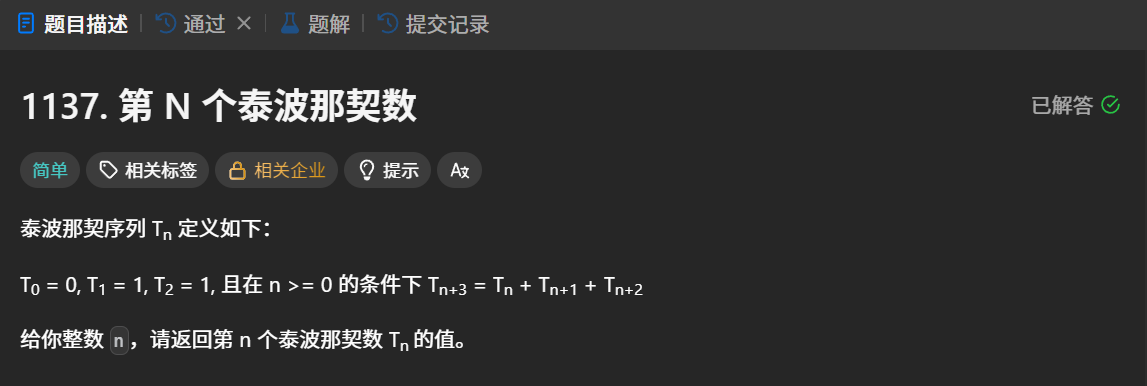
题目示例:
算法原理(动态规划):
思路:
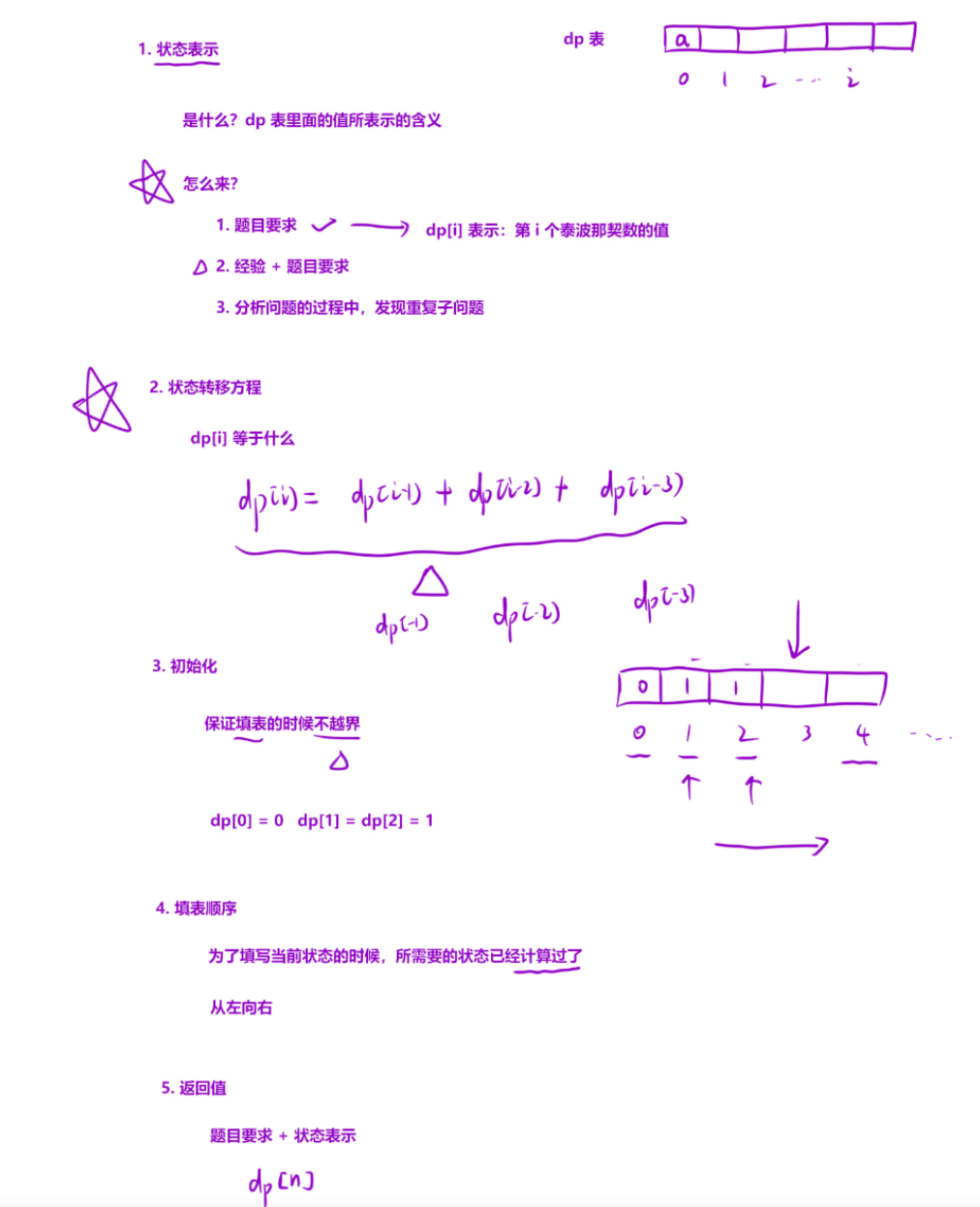
1. 状态表示 :
这道题可以【根据题目要求】直接定义出状态表示:
dp[i]表示:第i个泰波拉契数的值
2. 状态转移方程 :
题目已经很贴心的告诉了我们:dp[i] = dp[i-1] + dp[i-2] + dp[i-3]
3. 初始化
从我们的递推公式可以看出,dp[i]在 i=0以及i=1 的时候是没有办法进行推导的,因为dp[-2] 或 dp[-1] 不是一个有效的数据。因此我们需要在填表之前,将 0,1,2位置的值初始化。题目中已经告诉我们dp[0] = 0,dp[1] = dp[2] =1。
4. 填表顺序
毫无疑问是【从左往右】。
5. 返回值
应该返回 **dp[n]**的值。
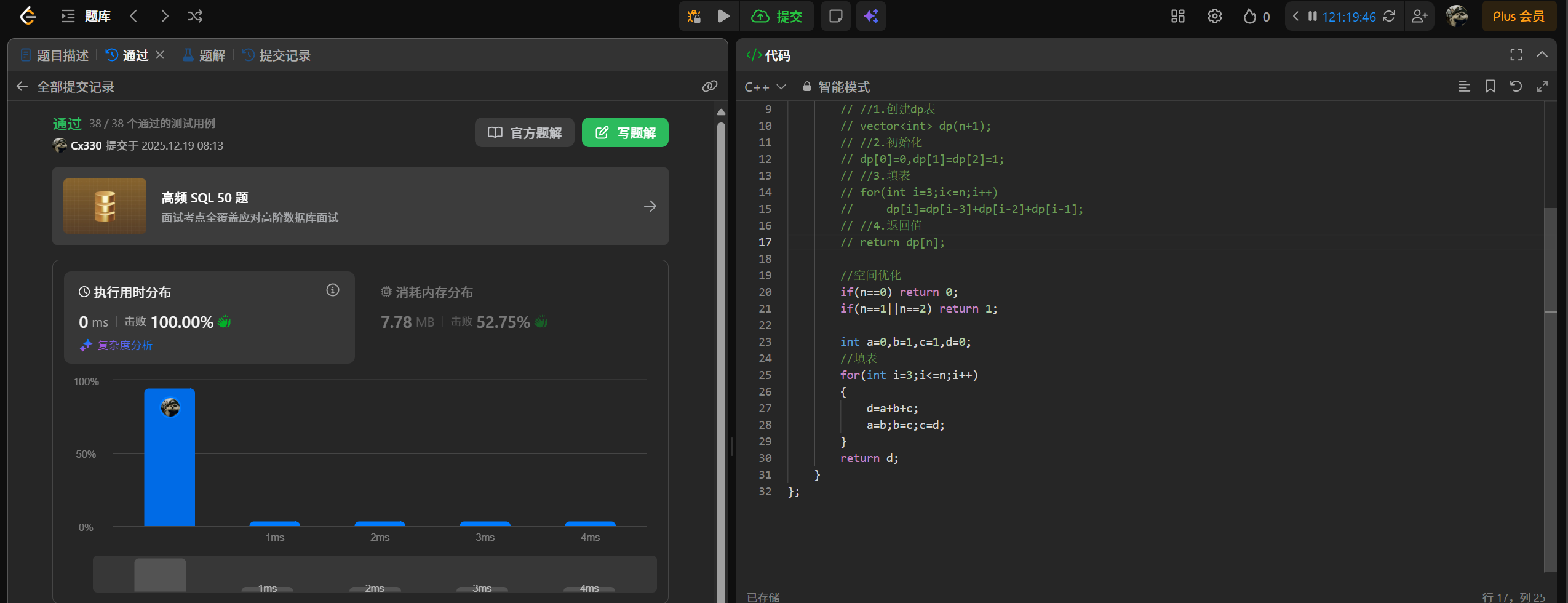
解法代码(C++):
cpp
class Solution
{
public:
int tribonacci(int n)
{
// //处理边界情况
// if(n==0) return 0;
// if(n==1||n==2) return 1;
// //1.创建dp表
// vector<int> dp(n+1);
// //2.初始化
// dp[0]=0,dp[1]=dp[2]=1;
// //3.填表
// for(int i=3;i<=n;i++)
// dp[i]=dp[i-3]+dp[i-2]+dp[i-1];
// //4.返回值
// return dp[n];
//空间优化
if(n==0) return 0;
if(n==1||n==2) return 1;
int a=0,b=1,c=1,d=0;
//填表
for(int i=3;i<=n;i++)
{
d=a+b+c;
a=b;b=c;c=d;
}
return d;
}
};
空间优化根据滚动数组来进行模拟优化
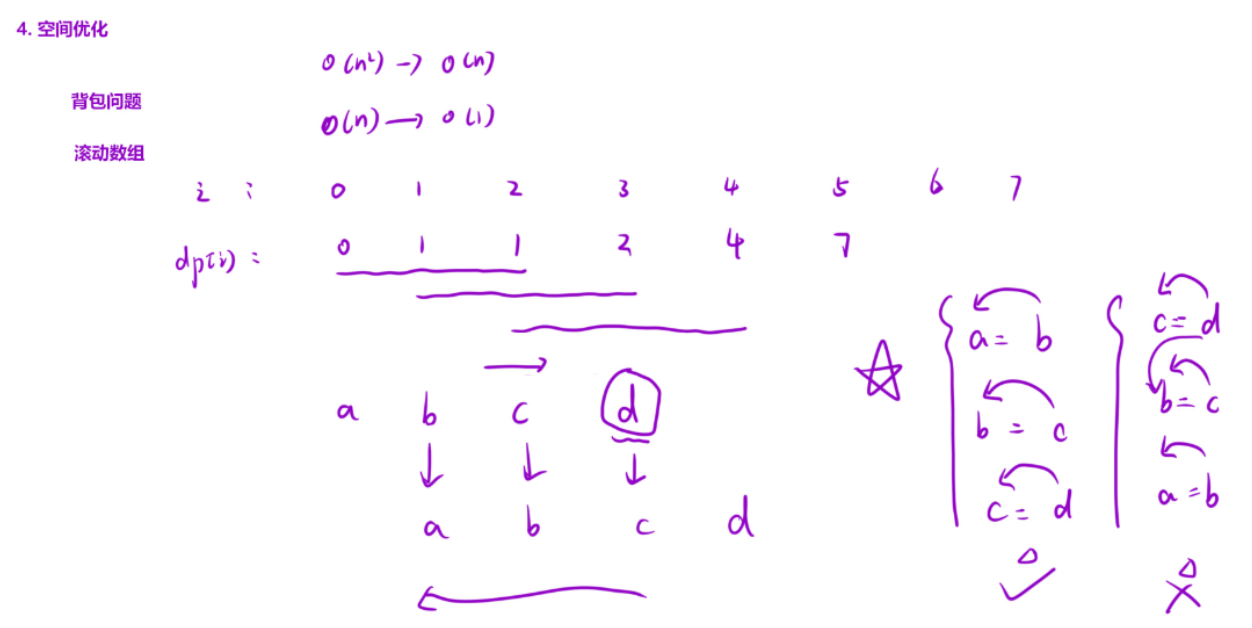
博主手记(字体还请见谅哈):

02.三步问题
题目链接:
题目描述:
题目示例:

算法原理(动态规划):
思路:
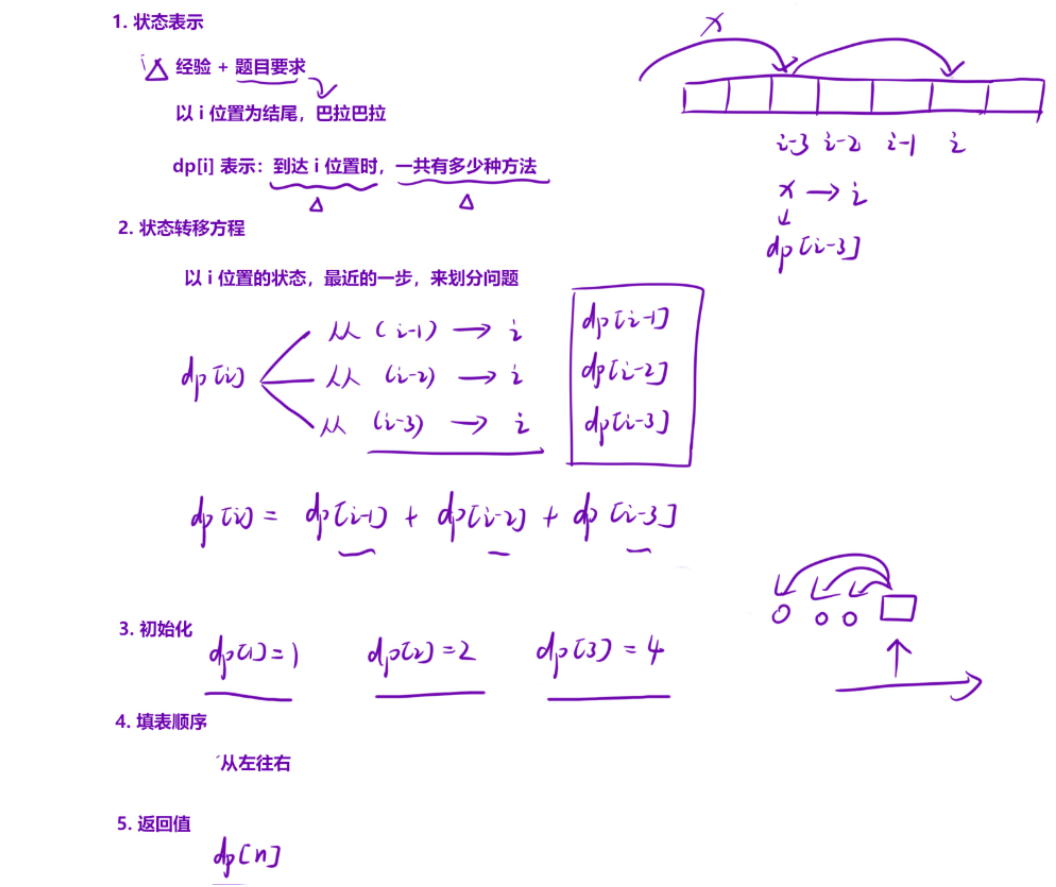
1. 状态表示 :
这道题可以根据【经验+题目要求】直接定义出状态表示:
dp[i]表示:到达i 位置时,一共有多少种方法。
2. 状态转移方程 :
以 i 位置状态的最近的一步,来分情况讨论:
如果 **dp[i]**表示小孩上第 i 阶楼梯的所有方式,那么他应等于所有上一步的方式之和:
- 上一步上一级台阶:dp[i] += dp[i-1];
- 上一步上两级台阶:dp[i] += dp[i-2];
- 上一步上三级台阶:dp[i] += dp[i-3];
综上所述,dp[i] = dp[i-1] + dp[i-2] + dp[i-3]。
需要注意的是,这道题目说,由于结果可能很大,需要对结果取模。
在计算的时候,三个值全部加起来再取模是不行的,大家可以自己取试试。对于这类问题,我们每计算一次(两个数相加/乘等),都需要取一次模。否则,万一发生了溢出,我们的答案就错了。
3. 初始化
从我们的递推公式可以看出,dp[i] 在 i=0,i=1 以及 i=2 的时候是没有办法进行推导的,因为dp[-3] dp[-2]或dp[-1] 不是一个有效的数据。
因此我们需要在填表之前,将 1,2,3 位置的值初始化。
根据题意,dp[1] = 1,dp[2] = 2,dp[3] = 4。
4. 填表顺序
毫无疑问是【从左往右】。
5. 返回值
应该返回 dp[n] 的值。
解法代码(C++):
bash
class Solution
{
const int MOD=1e9+7;
public:
int waysToStep(int n)
{
// if(n==1||n==2) return n;
// if(n==3) return 4;
// //1.创建dp表
// vector<int> dp(n+1);
// //2.初始化
// dp[1]=1,dp[2]=2,dp[3]=4;
// //3.填表
// for(int i=4;i<=n;i++)
// dp[i]=((dp[i-1]+dp[i-2])%MOD+dp[i-3])%MOD;
// return dp[n];
//空间优化
if(n==1||n==2) return n;
if(n==3) return 4;
int a=1,b=2,c=4,d=0;
//填表
for(int i=4;i<=n;i++)
{
d=((a+b)%MOD+c)%MOD;
a=b;b=c;c=d;
}
return d;
}
};博主手记(字体还请见谅哈):

结尾:
总结:本文分享了两个动态规划算法题的解题思路与代码实现。第一个是第N个泰波拉契数问题,通过状态转移方程dp[i]=dp[i-1]+dp[i-2]+dp[i-3]求解,并给出了空间优化方案。第二个是三步问题,分析上台阶的不同方式得出状态转移方程dp[i]=dp[i-1]+dp[i-2]+dp[i-3],强调取模运算的重要性。两题都采用从左往右填表顺序,并提供C++实现代码及空间优化版本