小白从零开始勇闯人工智能：机器学习初级篇（线性回归与逻辑回归）

引言

本章我们来学习机器学习中另两种经典算法：线性回归和逻辑回归。线性回归是一种用于预测连续数值的算法。它通过寻找特征与目标值之间的线性关系（即拟合一条直线或超平面）来进行预测，其输出可以是任意实数。逻辑回归虽然名为"回归"，但实际上是一种用于解决二分类问题的算法。它通过一个Sigmoid函数将线性回归的输出映射到(0,1)之间，将其解释为样本属于某个类别的概率。

一、线性回归详解

1、什么是线性回归？

线性回归是一种通过建立自变量与因变量之间的线性关系来进行预测的统计模型。其基本形式可以表示为：y = β₀ + β₁x₁ + β₂x₂ + ... + βₙxₙ + ε。在方程中，y代表因变量（即我们希望预测的连续值），x₁, x₂, ..., xₙ代表一系列自变量（用于预测的特征），β₀, β₁, ..., βₙ是模型的参数，其中 β₀为截距，其他β值代表每个特征对目标值的影响权重，而ε则代表误差项，用于捕捉模型无法解释的随机波动。该模型的目标是找到一组最优的参数β，使得预测值ŷ与真实值y之间的误差最小。

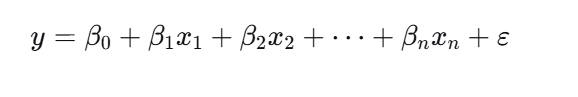
2、一元线性回归与多元线性回归

一元线性回归和多元线性回归是线性模型中两种基本形式，前者只涉及一个自变量，其模型可表示为：

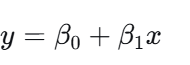
后者则包含两个或以上的自变量，例如：

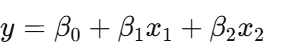
它们都通过线性关系来描述因变量与一个或多个自变量之间的关联。

3、损失函数：量化预测误差

损失函数的作用是量化模型预测值与真实值之间的误差，在线性回归中，最常用的损失函数是均方误差（MSE），其数学表达式为 :

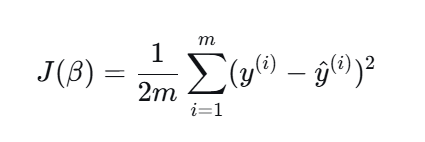
其中m代表样本数量，是第i个样本的真实值，是模型对应的预测值，而优化模型的目标就是通过调整参数来最小化这个损失函数的值。

4、最小二乘法与梯度下降

在线性回归中，为了找到能使损失函数最小化的模型参数，主要采用两种优化方法：其中一种是最小二乘法，它通过解析解公式：

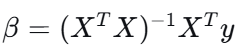
直接计算出最优参数；另一种方法是梯度下降，它通过迭代方式逐步调整参数以逼近最优解，这种方法尤其适用于自变量维度高或数据集规模很大的情况。

5、误差项分析

要想保障线性回归模型的完整性和可靠性可以通过两方面：一方面是误差项分析，其中模型未能捕捉的随机波动由误差项表示，通常假设它服从均值为0、方差恒定的正态分布，这确保了参数估计的统计性质，另一方面则依赖于一系列模型评估指标，例如R平方、调整R平方、均方误差（MSE）等。

6、模型评估指标

我们通常会借助几个关键指标来评估线性回归模型的效果：首先，相关系数（r）用于量化两个变量之间线性相关的方向与强度，其次，拟合优度（R²）反映了模型所能解释的数据变异比例，其值越接近1，说明模型对数据的解释能力越强，最后，为了避免在多元回归中因自变量数量增加而导致的虚假拟合提升，还会参考调整R²，它对自变量个数进行了校正，从而稳健的评估模型的实际表现。

7、假设检验

在线性回归的统计推断中，假设检验是评估模型可靠性的关键步骤，主要包括两种检验：F检验用于判断模型整体是否统计显著，即检验所有自变量的联合作用是否对因变量有显著解释力，而T检验则用于评估单个自变量的回归系数是否显著不为零，以此判断该特定变量是否对模型有独立的影响。

8、数据预处理：标准化

在构建线性回归模型前，对数据进行标准化是重要的预处理步骤，其作用是消除不同特征之间由于取值范围差异所造成的影响，常用的方法包括0-1标准化（Min-Max Scaling），它将原始数据线性变换到[0, 1]区间，以及Z标准化（Standardization），该方法将数据转换为均值为0、标准差为1的分布，从而使不同特征具有可比性，并有助于提升许多优化算法的收敛效率与稳定性。

9、正则化：防止过拟合

正则化是机器学习中用于防止模型过拟合的关键，过拟合指的是模型在训练数据上表现优异，却在未见过的新数据上预测能力出现明显下降的现象，为了改善这一问题，常见的正则化方法如L1正则化和L2正则化通过在损失函数中引入对模型参数的惩罚项，来约束参数的幅度或促使部分参数趋近于零，从而简化模型结构、降低模型复杂度，提升模型的泛化能力。

二、逻辑回归详解

1、逻辑回归是"回归"吗？

逻辑回归虽然名称中带有回归二字，但逻辑回归本质上是一种广泛应用于二分类问题（例如判断是否患病）的分类算法，其名称源于它使用了类似于线性回归的线性组合形式，但逻辑回归是通过Sigmoid函数将线性结果映射到(0,1)区间，输出一个代表类别的概率值。

2、Sigmoid函数：将输出转换为概率

在逻辑回归模型中，Sigmoid函数的作用是将线性回归模型产生的任意实数输出非线性地映射到 (0, 1) 区间内，该映射结果被直接解释为样本属于正类的预测概率，使逻辑回归得以基于概率阈值（通常为0.5）进行明确的分类决策。其具体形式为：

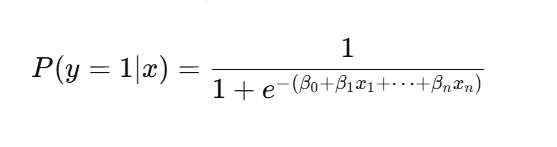
3、损失函数：交叉熵损失

逻辑回归的训练目标由交叉熵损失函数来定义的，该函数是专门用于衡量模型预测的概率分布与真实的类别标签之间的差异，其数学表达式为：

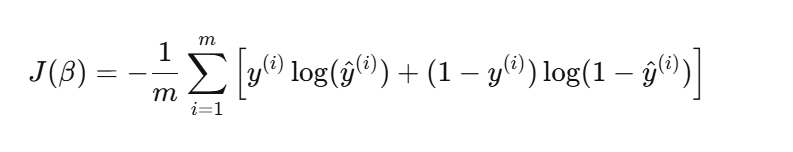
其中m为样本数量，是第i个样本的真实标签（通常取0或1），则是模型通过Sigmoid函数预测出的该样本属于正类的概率，通过最小化这一损失函数，模型能够有效地调整参数 ，使预测概率尽可能接近真实情况。

4、模型评估：混淆矩阵与指标

逻辑回归模型的性能评估依赖于基于混淆矩阵的指标，混淆矩阵通过统计真正例（TP）、假正例（FP）、假负例（FN）和真负例（TN）四个基础数值，提供了模型分类结果的详细划分，在此基础上，准确率（模型预测正确的总体比例，即 ）虽然直观，但在类别不平衡时可能具有误导性从而不准确，因此我们还需要借助精确率（即查准率，衡量被预测为正类的样本中实际为正的比例，公式为）和召回率（即查全率，衡量实际为正类的样本中被正确预测的比例，公式为）来分别评估，而F1-Score作为精确率与召回率的调和平均数，则综合了这两者，提供了一个在需要平衡精确率与召回率时更具参考价值的评估指标。

5、过拟合与欠拟合

在机器学习模型训练过程中，过拟合与欠拟合是两种常见问题：欠拟合是指模型结构过于简单或学习能力不足，导致无法有效捕捉数据中潜在的基本规律，通常在训练集和测试集上都表现不佳；而过拟合则是指模型过于复杂，过度学习了训练数据中的细节甚至噪声，导致其在训练集上表现优异，但在新的、未见过的测试数据上表现能力很差，一个理想的模型需要在复杂度和简单性之间取得平衡，以在偏差（欠拟合）和方差（过拟合）之间找到最优解。

6、处理类别不平衡：SMOTE过采样

在处理分类问题，特别是遇到正负样本数量差异明显的类别不平衡情况时，直接训练模型往往会导致其对多数类产生偏好。为了解决这一问题，SMOTE（合成少数类过采样技术）是一种常用的方法，它并非是简单复制少数类样本，而是通过分析现有少数类样本的k近邻，并在这些样本点之间进行线性插值来人工合成新的、合理的少数类样本，从而增加少数类在训练集中的代表性，以帮助模型更好地学习其分布特征，最终提升模型（如逻辑回归等）对少数类别的识别与召回能力。

四、代码实践：使用sklearn实现线性回归与逻辑回归

1、一元线性回归示例

1).导入所需库

import pandas as pd          # 数据处理和分析
import numpy as np           # 数值计算
import matplotlib.pyplot as plt  # 数据可视化
from sklearn.linear_model import LinearRegression  # 线性回归模型
from sklearn.model_selection import train_test_split  # 数据集划分
from sklearn.metrics import mean_squared_error, r2_score  # 评估指标

2).读取数据

data = pd.read_csv("data.csv")  # 读取名为"data.csv"的数据文件
X = data[['广告投入']]  # 特征变量（自变量），双括号返回DataFrame格式
y = data['销售额']     # 目标变量（因变量），单括号返回Series格式

3).划分训练集与测试集

X_train, X_test, y_train, y_test = train_test_split(
    X, y, 
    test_size=0.2,     # 测试集占20%，训练集占80%
    random_state=42    # 随机种子，确保每次划分结果一致
)

4).创建和训练模型

# 创建线性回归模型实例
model = LinearRegression(fit_intercept=True)  # fit_intercept=True表示计算截距

# 训练模型：找到最佳拟合线 y = aX + b
model.fit(X_train, y_train)  # 通过最小二乘法计算斜率和截距

5).预测和评估

# 使用训练好的模型进行预测
y_pred = model.predict(X_test)  # 对测试集进行预测

# 输出模型参数和评估指标
print("斜率:", model.coef_)        # 回归系数（斜率a）
print("截距:", model.intercept_)   # 截距b
print("MSE:", mean_squared_error(y_test, y_pred))  # 均方误差
print("R²:", r2_score(y_test, y_pred))             # 决定系数

6).可视化结果

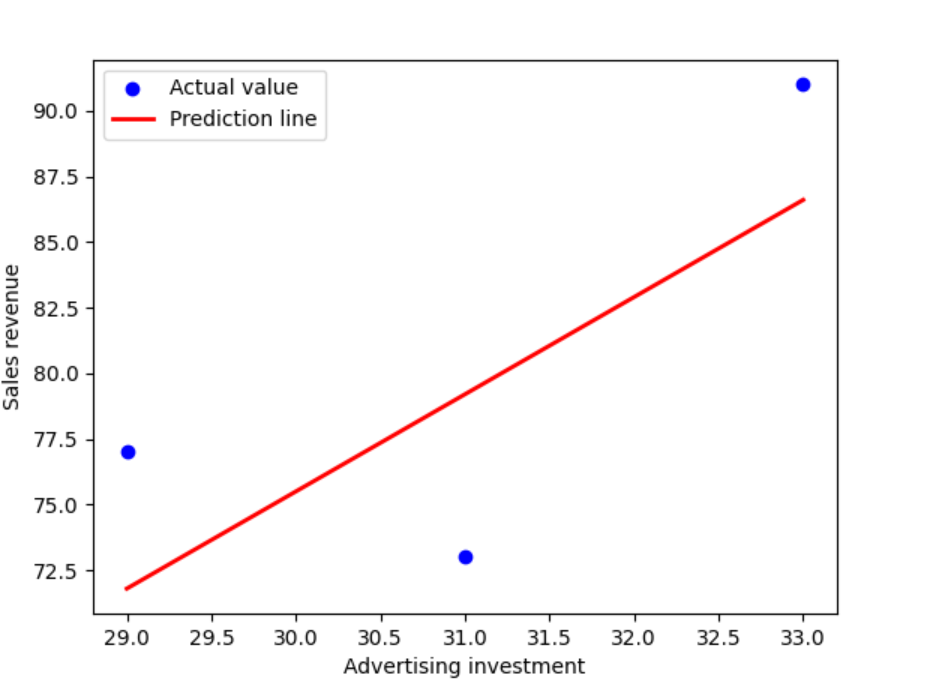
# 创建散点图和回归线
plt.scatter(X_test, y_test, color='blue', label='Actual value')  # 实际值的散点
plt.plot(X_test, y_pred, color='red', linewidth=2, label='Prediction line')  # 预测线
plt.xlabel('Advertising investment')  # x轴标签
plt.ylabel('Sales revenue')    # y轴标签
plt.legend()           # 显示图例
plt.show()             # 显示图形

7).结果展示

2、逻辑回归示例

1).导入必要的库

from sklearn.datasets import make_classification  # 生成模拟数据集
from sklearn.model_selection import train_test_split  # 数据集划分
from sklearn.linear_model import LogisticRegression  # 逻辑回归模型
from sklearn.metrics import confusion_matrix, classification_report, accuracy_score  # 评估指标
from sklearn.preprocessing import StandardScaler  # 数据标准化

2).创建二分类数据集

X, y = make_classification(
    n_samples=1000,   # 生成1000个样本
    n_features=10,    # 每个样本有10个特征
    n_informative=5,  # 其中5个特征对分类有实际信息量
    n_redundant=2,    # 2个特征是冗余特征（由有信息量特征组合而成）
    n_classes=2,      # 二分类问题
    random_state=42   # 固定随机种子，确保结果可重现
)

3).划分训练集和测试集

X_train, X_test, y_train, y_test = train_test_split(
    X, y, 
    test_size=0.3,    # 30%作为测试集
    random_state=42   # 固定随机划分
)

4).数据标准化

scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)  # 计算训练集均值和标准差并转换
X_test_scaled = scaler.transform(X_test)        # 用训练集的参数转换测试集

5).创建和训练逻辑回归模型

log_model = LogisticRegression()  # 创建逻辑回归分类器
log_model.fit(X_train_scaled, y_train)  # 用标准化后的训练数据训练模型

6).在测试集上进行预测

y_pred = log_model.predict(X_test_scaled)  # 预测测试集标签

7).模型评估

# 1. 准确率
print("准确率:", accuracy_score(y_test, y_pred))
# 正确预测的样本数占总样本数的比例
# 2. 混淆矩阵
print("混淆矩阵:\n", confusion_matrix(y_test, y_pred))
"""
混淆矩阵结构:
[[TN  FP]
 [FN  TP]]
TN: 真阴性 (实际为0，预测为0)
FP: 假阳性 (实际为0，预测为1)
FN: 假阴性 (实际为1，预测为0)
TP: 真阳性 (实际为1，预测为1)
"""
# 3. 分类报告
print("分类报告:\n", classification_report(y_test, y_pred))
"""
包含:
- Precision (精确率): TP/(TP+FP)，预测为正例的样本中实际为正例的比例
- Recall (召回率): TP/(TP+FN)，实际为正例的样本中被正确预测的比例
- F1-score: Precision和Recall的调和平均数
- Support: 每个类别的样本数量
"""

8).结果展示

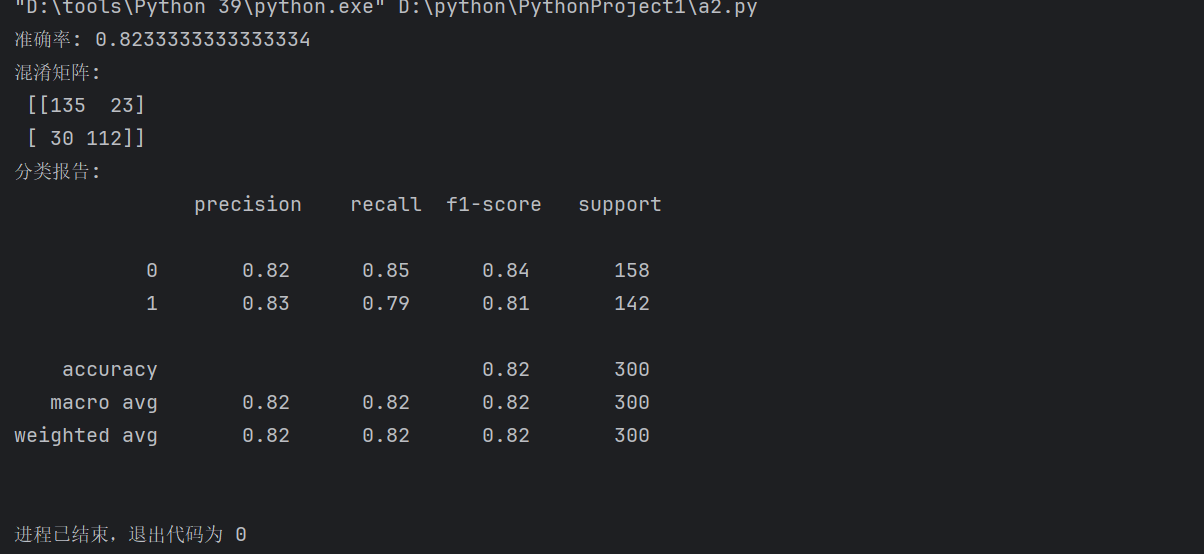
在本篇文章中我们基本了解了线性回归和逻辑回归，在下一章中我们将学习机器学习中另两种常见的算法：决策树和随机森林。