循环队列：出队

晨晖22025-12-20 11:03

参考视频

5.双向链表_栈_队列_哔哩哔哩_bilibili1小时15分钟到最后（顺序队列的知识）

6.循环队列_讲题_递归_哔哩哔哩_bilibili前20分钟

题目

复制代码 
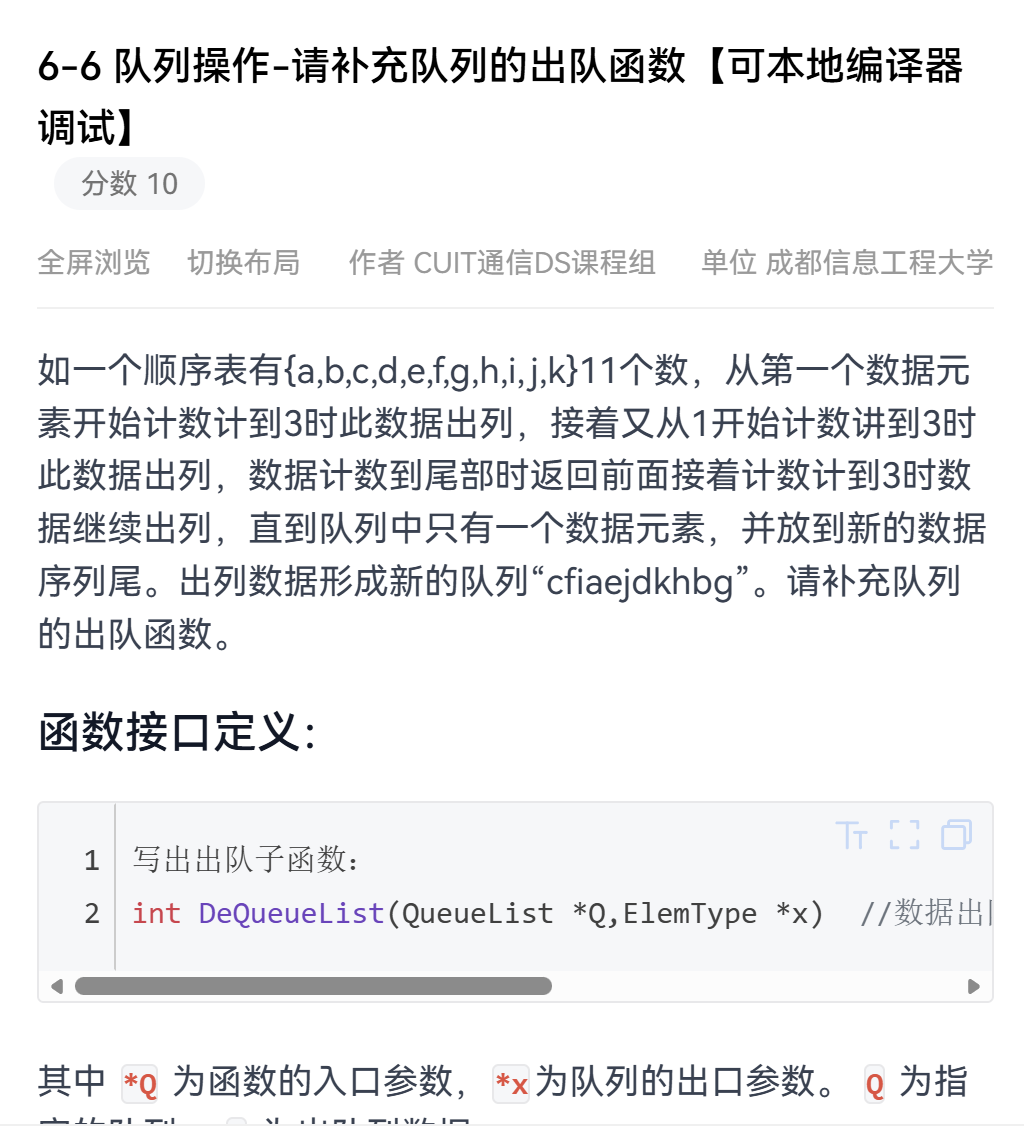
#include <stdio.h>
#include <string.h>
#include <stdlib.h>

#define  ElemType  char
#define  NumSize   100
typedef struct 
{
    ElemType dat[NumSize]; //顺序队列
    int real,front;          //队列首、尾指针
}QueueList;
int initQueueList(QueueList *Q) //初始化顺序栈
{
    Q->real =0;
    Q->front =0;
    return (1);
}

int LengthQueueList(QueueList Q) //求队列的长度
{ 
    int i;
    i= (Q.real - Q.front + NumSize) % NumSize; //求队列中数据的总长度
    return(i);//返回队列数据的总数  说明：队列中数据总数 = 最大值 - 1 表明队列满
}

int ListQueueEmpty(QueueList Q)
{
    if(Q.real == Q.front )
    {
        return(0); //队列空返回0
    }    
    return (1);//不空返回1
} 

int ENQueueList(QueueList *Q,ElemType x)//数据入队
{
    
    if((Q->real +1) % NumSize ==  Q->front)
    {
        printf("队列满失败\n");
        return 0;//队列满返回0
    }    
    Q->dat[Q->real] =x;//x入队
    Q->real =( Q->real + 1)% NumSize; //队尾指针加1
    return (1);//入队成功返回1
}
/* 本题要求子函数------出队列 */
int DeQueueList(QueueList *Q,ElemType *x);
int main(void)
{
    int  i;
    ElemType x;    
    QueueList q;//定义队列q        
    initQueueList(&q);//初始化队列
    // 输入11个字符的字符串
    for (i = 0; i < 11; i++)//数据入队列
    {
        x = getchar();        
        ENQueueList(&q, x);
    }
    i = 0;
    while (LengthQueueList(q) != 1) //队列中数据个数据不为1循环执行
    {
        DeQueueList(&q, &x);
            ++i;
        if (i < 3)    ENQueueList(&q, x);
        else
        {    i = 0;
            printf("%c",x);//出列的数据元素一个一个地显示出来
        }
    }
    DeQueueList(&q, &x);//最后一个数据出队 且出队数据放到x中
    printf("%c", x);//显示最后一个数据元素
    return 0;
}

/* 请在这里填写答案 */

解析

普通的循环队列的出队，解决这个需要队列的前置知识，建议参考视频和下面笔记

答案

复制代码 
int DeQueueList(QueueList *Q,ElemType *x){
    if(Q->front==Q->real){
        return 0;
    }
    *x=Q->dat[Q->front];
    Q->front=(Q->front+1)%NumSize;
    return 1;
}

前置知识

一、队列的核心概念

1. 基本定义

队列是一种线性数据结构，只允许在队尾（Rear） 插入新元素（入队），在队头（Front） 删除元素（出队），整体遵循 "先进先出（FIFO, First In First Out）" 原则。可以类比生活中的排队：先到的人先办理业务，后到的人只能排在队尾。

2. 核心特点

  • 操作受限：仅支持两端操作，队尾入、队头出，中间元素不可直接访问 / 修改；
  • 顺序性：元素的出队顺序与入队顺序完全一致；
  • 常见分类：
    • 普通顺序队列：基于数组实现，易出现 "假溢出" 问题；
    • 循环队列：对普通顺序队列的优化，通过取模实现数组空间的循环利用，解决假溢出。

二、队列的基础结构定义

无论普通顺序队列还是循环队列，都可以基于数组实现，先定义统一的结构体（需提前宏定义数组最大容量）：

复制代码 
// 宏定义队列的最大容量
#define MAXSIZE 100
// 定义队列元素类型（可根据需求修改，如char、int等）
typedef int ElemType;

// 队列的结构体定义
typedef struct Queue {
    ElemType data[MAXSIZE];  // 存储队列元素的数组
    int front;               // 队头指针：指向队头元素的位置
    int rear;                // 队尾指针：指向队尾元素的下一个位置
} Queue;

关键说明：

  • front 和 rear 初始值均为 0，此时 front == rear 表示队列为空；
  • 数组 data 是队列的底层存储容器，MAXSIZE 决定队列能容纳的最大元素数。

三、队列的通用基础操作

1. 队列初始化

功能

将队列初始化为空状态，是使用队列的第一步。

复制代码 
// 初始化队列：将队头、队尾指针置0
void initQueue(Queue *Q) {
    Q->front = 0;  // 队头指针归0
    Q->rear = 0;   // 队尾指针归0
}
可视化展示

假设 MAXSIZE=5，初始化后队列的状态如下（□ 表示空位置，front/rear 用箭头标注位置）：

plaintext

复制代码 
数组索引： 0    1    2    3    4
data：    □    □    □    □    □
          ↑
        front
          ↑
        rear

说明 ：初始化后 Q->front == Q->rear，这是判断队空的核心条件。

2. 队列判空

功能：判断队列是否为空，为空返回 1，非空返回 0（新手易混淆返回值逻辑，需注意）。

复制代码 
// 判空函数：front == rear 代表队空
int isEmpty(Queue *Q) {
    if (Q->front == Q->rear) {
        return 1;  // 队空，返回1
    } else {
        return 0;  // 队非空，返回0
    }
}

四、循环队列的核心操作（解决假溢出）

普通顺序队列的 "假溢出" 是指：数组未存满，但队尾指针已到数组末尾，无法继续入队。循环队列通过 "取模运算" 让指针绕回数组开头，彻底解决该问题。

1. 循环队列入队

功能

将元素插入队尾，成功返回 1，队列满则返回 0（新手易写错判满条件）。

复制代码 
// 循环队列入队函数
int enqueueCircular(Queue *Q, ElemType e) {
    // 循环队列判满条件：(rear + 1) % MAXSIZE == front（预留一个空位避免与队空混淆）
    if ((Q->rear + 1) % MAXSIZE == Q->front) {
        printf("循环队列已满，入队失败\n");
        return 0;
    }
    // 将元素存入队尾指针指向的位置
    Q->data[Q->rear] = e;
    // 队尾指针后移（取模实现"循环"，超出数组长度则绕回开头）
    Q->rear = (Q->rear + 1) % MAXSIZE;
    return 1;  // 入队成功
}
可视化展示（以 MAXSIZE=5 为例）

  • 初始状态：front=0，rear=0，队列为空；

  • 入队元素 1：data[0]=1，rear=(0+1)%5=1

    plaintext

    复制代码 
    数组索引： 0    1    2    3    4
data：    1    □    □    □    □
          ↑    ↑
        front  rear

  • 继续入队 2、3、4：rear=4

    plaintext

    复制代码 
    数组索引： 0    1    2    3    4
data：    1    2    3    4    □
          ↑                   ↑
        front                rear

  • 此时队未满（(4+1)%5=0 == front 才满），再入队 5：data[4]=5，rear=(4+1)%5=0

    plaintext

    复制代码 
    数组索引： 0    1    2    3    4
data：    1    2    3    4    5
          ↑                   ↑
        front                rear(rear=0)

    此时 (rear+1)%5=1 != front，仍可入队？不，此时 (0+1)%5=1≠0，但实际数组已存满？注意：循环队列预留 1 个空位判满，所以上述状态中，rear=0 时，(0+1)%5=1≠front=0，但再入队会触发 (0+1)%5=1≠0，直到入队后 rear=4，(4+1)%5=0=front 才判满。

新手常见错误 ：直接用 Q->rear == MAXSIZE 判满，忽略循环特性，导致数组空间浪费。

2. 循环队列出队

功能

从队头取出元素并存储到指定变量，成功返回 1，队空则返回 0（最易踩指针移动错误）。

复制代码 
// 循环队列出队函数
int dequeueCircular(Queue *Q, ElemType *e) {
    // 先判断队列是否为空
    if (Q->front == Q->rear) {
        printf("循环队列为空，出队失败\n");
        return 0;
    }
    // 取出队头元素
    *e = Q->data[Q->front];
    // 队头指针后移（取模实现循环，核心！新手易漏+1）
    Q->front = (Q->front + 1) % MAXSIZE;
    return 1;  // 出队成功
}
可视化展示（承接上述入队 5 后的状态：front=0，rear=0？不，入队 5 后是 front=0，rear=0？修正：入队 1、2、3、4 后 rear=4，入队 5 后 data[4]=5，rear=(4+1)%5=0，此时状态：

plaintext

复制代码 
数组索引： 0    1    2    3    4
data：    1    2    3    4    5
          ↑                   ↑
        front(0)            rear(0)

  • 出队元素 1：*e=1，front=(0+1)%5=1

    plaintext

    复制代码 
    数组索引： 0    1    2    3    4
data：    1    2    3    4    5
             ↑              ↑
           front(1)        rear(0)

  • 再出队元素 2：*e=2，front=(1+1)%5=2

    plaintext

    复制代码 
    数组索引： 0    1    2    3    4
data：    1    2    3    4    5
                  ↑         ↑
                front(2)   rear(0)

    此时队仍非空（front≠rear），可继续出队，直到 front=0 且 rear=0 时队空。

新手致命错误 ：仅写 Q->front = Q->front % MAXSIZE，未加 1，导致队头指针永远不移动，重复取出同一个元素。

五、普通顺序队列（处理假溢出）

普通顺序队列不做循环处理，队尾指针到达数组末尾后，需通过 "元素前移" 利用队头空出的空间，解决假溢出问题。

1. 假溢出调整函数

功能

当队尾越界但队头有空位时，将所有元素前移，空出开头空间。

复制代码 
// 假溢出调整：前移元素，复用队头空出的空间
int adjustQueue(Queue *Q) {
    if (Q->front > 0) {  // 队头有空闲空间
        int step = Q->front;  // 前移的步数
        // 将元素从front位置移到数组开头
        for (int i = Q->front; i < Q->rear; i++) {
            Q->data[i - step] = Q->data[i];
        }
        // 更新指针：队头归0，队尾同步前移
        Q->front = 0;
        Q->rear = Q->rear - step;
        return 1;  // 调整成功
    } else {
        printf("队列真满，无空间可调整\n");
        return 0;  // 数组完全存满，调整失败
    }
}
可视化展示（假溢出调整）

假设 MAXSIZE=5，初始入队 1、2、3 后出队 1、2，状态如下：

plaintext

复制代码 
数组索引： 0    1    2    3    4
data：    □    □    3    □    □
                ↑         ↑
              front=2    rear=3

此时入队 4、5，rear=5（超出 MAXSIZE=5），触发假溢出调整：

  • step=front=2，元素前移 2 步：data[0]=3、data[1]=4、data[2]=5；
  • 指针更新：front=0，rear=3；调整后状态：

plaintext

复制代码 
数组索引： 0    1    2    3    4
data：    3    4    5    □    □
          ↑         ↑
        front      rear

2. 普通顺序队列入队

功能

插入元素到队尾，遇假溢出则先调整再入队。

复制代码 
// 普通顺序队列入队（处理假溢出）
int enqueueNormal(Queue *Q, ElemType e) {
    // 队尾超出数组范围，尝试调整
    if (Q->rear >= MAXSIZE) {
        if (!adjustQueue(Q)) {  // 调整失败则入队失败
            return 0;
        }
    }
    // 元素入队，队尾指针后移
    Q->data[Q->rear] = e;
    Q->rear++;
    return 1;  // 入队成功
}
可视化展示

初始状态 front=0，rear=0：

  • 入队 1：data[0]=1，rear=1

    plaintext

    复制代码 
    数组索引： 0    1    2    3    4
data：    1    □    □    □    □
          ↑    ↑
        front  rear

  • 入队 2、3、4：rear=4

    plaintext

    复制代码 
    数组索引： 0    1    2    3    4
data：    1    2    3    4    □
          ↑                   ↑
        front                rear

  • 入队 5：data[4]=5，rear=5（此时 rear >= MAXSIZE）

    plaintext

    复制代码 
    数组索引： 0    1    2    3    4
data：    1    2    3    4    5
          ↑                     
        front                   rear=5（越界）

    若再入队 6，触发调整（但 front=0，无空闲空间，调整失败，入队失败）。

3. 普通顺序队列出队

功能

从队头取出元素并返回，队空则返回错误标识（0）。

复制代码 
// 普通顺序队列出队
ElemType dequeueNormal(Queue *Q) {
    // 判空
    if (Q->front == Q->rear) {
        printf("普通队列为空，出队失败\n");
        return 0;  // 队空返回错误标识
    }
    // 取出队头元素，队头指针后移
    ElemType e = Q->data[Q->front];
    Q->front++;
    return e;  // 返回出队元素
}
可视化展示（承接入队 1、2、3、4、5 后的状态：front=0，rear=5）

  • 出队 1：e=1，front=1

    plaintext

    复制代码 
    数组索引： 0    1    2    3    4
data：    1    2    3    4    5
             ↑                ↑
           front=1           rear=5

  • 出队 2：e=2，front=2

    plaintext

    复制代码 
    数组索引： 0    1    2    3    4
data：    1    2    3    4    5
                  ↑           ↑
                front=2      rear=5

    此时数组前 2 个位置空出，但 rear=5 仍越界，再入队需触发假溢出调整。

六、新手常见错误避坑指南

  1. 循环队列指针移动：出队时必须 front = (front + 1) % MAXSIZE，仅取模不加 1 会导致指针静止；
  2. 判满 / 判空混淆：循环队列判满是 (rear+1)%MAXSIZE == front，判空是 front == rear，新手易颠倒；
  3. 普通队列假溢出：直接认为 rear >= MAXSIZE 就是队满，忽略队头空出的空间；
  4. 指针操作未判空：调用出队函数前未检查队列是否为空，导致访问无效元素。

总结

  1. 队列的核心是 "先进先出"，循环队列通过取模解决普通顺序队列的假溢出问题，是实际开发中更常用的实现方式；
  2. 循环队列的关键是指针的 "循环移动"（取模运算），判满需预留一个空位避免与判空条件冲突，通过可视化能清晰看到指针的移动规律；
  3. 普通顺序队列需通过元素前移处理假溢出，但效率低于循环队列，仅适用于简单场景；
  4. 初始化、入队、出队的可视化能直观体现指针与数组元素的关系，是理解队列逻辑的关键，新手需重点掌握指针的更新规则。

手写笔记

如下图所示，rear指向队尾元素的下一个

顺序队列易出现假溢出，所以有了循环队列，下面图片解释假溢出和入队

循环队列解决了上述问题

相关推荐
LYFlied3 小时前
【每日算法】LeetCode 70. 爬楼梯：从递归到动态规划的思维演进
算法·leetcode·面试·职场和发展·动态规划
最晚的py3 小时前
聚类的评估方法
人工智能·算法·机器学习
业精于勤的牙3 小时前
浅谈：算法中的斐波那契数（五）
算法·leetcode·职场和发展
液态不合群3 小时前
查找算法详解
java·数据结构·算法
代码游侠3 小时前
学习笔记——Linux进程间通信（IPC）
linux·运维·笔记·学习·算法
高洁013 小时前
DNN案例一步步构建深层神经网络（3）
python·深度学习·算法·机器学习·transformer
_dindong3 小时前
笔试强训：Week -8
开发语言·c++·算法
LYFlied4 小时前
【每日算法】LeetCode 105. 从前序与中序遍历序列构造二叉树
数据结构·算法·leetcode·面试·职场和发展
DanyHope4 小时前
LeetCode 206. 反转链表：迭代 + 递归双解法全解析
算法·leetcode·链表·递归·迭代
热门推荐
01GitHub 镜像站点02UV安装并设置国内源03Linux下V2Ray安装配置指南04安娜的档案(Anna’s Archive) 镜像网站/国内最新可访问入口（持续更新）05在VSCode配置Java开发环境的保姆级教程（适配各类AI编程IDE）06RedissonClient的配置解析07BongoCat - 跨平台键盘猫动画工具08jdk21下载、安装（Windows、Linux、macOS）09Open-AutoGLM Windows 安装部署教程10Labelme从安装到标注：零基础完整指南