超宽带脉冲无线电(Ultra Wideband Impulse Radio, UWB)简介
https://inatel.br/docentes/documents/dayan/Publications/43.pdf
1. IR‑UWB 的"天然形态":极短脉冲 → 极宽频谱 → 低功率谱密度
一个系统若满足"分数带宽(fractional bandwidth)大于 0.25",或"占用频谱宽度不小于 1.5 GHz",就属于 UWB 。分数带宽的计算按 −10 dB 发射点取上下边界频率 fH,fLf_H,f_LfH,fL,并:
Bf=2(fH−fL)fH+fL,fc=fH+fL2. B_f=\frac{2(f_H-f_L)}{f_H+f_L},\qquad f_c=\frac{f_H+f_L}{2}. Bf=fH+fL2(fH−fL),fc=2fH+fL.
其中BfB_fBf 衡量"相对带宽",而 fcf_cfc 用上下 −10 dB 点的平均值,作为"工作中心"。另外UWB 的定义并不强制必须用脉冲 ,而本文专讲"脉冲无线电 IR‑UWB",因为它的信号形态非常"极端":发射的是亚纳秒乃至皮秒级能量脉冲,于是时域极短带来频域极宽,且系统通常还要求极低 ERP(有效辐射功率),因此功率谱密度更容易压得很低。
2. 脉冲形状:从高斯到高斯单周期(monocycle),以及式 (1)(2) 背后到底是什么
2.1 "天线近似求导"这句话的数学含义
原文在 II‑A 里说:高斯脉冲易生成,因此常用;当把高斯脉冲加到理想发射天线 上时,由于天线的"导数行为"(derivative behavior),辐射电场中出现的会是高斯脉冲的导数,这就是经典的 Gaussian monocycle。论文把这个单周期直接写成(式 (1)):
p(t)=−2πfc texp{12[1−(2πfct)2]}.(1) p(t)=-2\pi f_c\, t \exp\left\{\frac12\left[1-(2\pi f_c t)^2\right]\right\}. \tag{1} p(t)=−2πfctexp{21[1−(2πfct)2]}.(1)
这条式子最值得抓住的是"结构"而非常数:它本质上是
p(t)∝t⋅e−(2πfct)2/2, p(t)\propto t\cdot e^{-(2\pi f_c t)^2/2}, p(t)∝t⋅e−(2πfct)2/2,
因此一定呈现"先负后正(或相反)的单次过零"波形:因为前面的 ttt 让信号关于 t=0t=0t=0 变号,而高斯因子给了一个平滑包络,把能量束在一个短时窗里。论文还提到:理想接收天线会对接收到的电场再做一次微分,因此负载上得到的是高斯脉冲的二阶导数(这解释了为什么工程里常见"单周期/双周期/多阶导数高斯脉冲"族)。
2.2 fc≈1/τf_c\approx 1/\taufc≈1/τ :时间缩放与频域展宽
fc=1/τf_c=1/\taufc=1/τ,其中 τ\tauτ 是脉冲的"近似持续时间"。这是一个典型的"量纲级"关系:若把 p(t)p(t)p(t) 在时间轴上压缩为 p(at)p(at)p(at),那么其频谱会被拉伸为 1∣a∣P(f/a)\frac{1}{|a|}P(f/a)∣a∣1P(f/a);时间越短,频谱越宽。式 (1) 里 2πfct2\pi f_c t2πfct 是自然的无量纲变量,所以 fcf_cfc 本质上就是"时间尺度"的倒数:ttt 轴的特征宽度 ∼1/fc\sim 1/f_c∼1/fc,于是脉冲持续时间量级 τ∼1/fc\tau\sim 1/f_cτ∼1/fc。
2.3 功率谱密度式 (2):为什么出现 (f/fc) e−(f/fc)2/2(f/f_c)\,e^{-(f/f_c)^2/2}(f/fc)e−(f/fc)2/2 这种形状
论文给出单周期的功率谱密度(写成归一化形式):
P(f)=(ffc)exp{12[1−(ffc)2]}.(2) P(f)=\left(\frac{f}{f_c}\right)\exp\left\{\frac12\left[1-\left(\frac{f}{f_c}\right)^2\right]\right\}. \tag{2} P(f)=(fcf)exp{21[1−(fcf)2]}.(2)
这背后有两个关键"频域操作":
第一,高斯在频域仍是高斯;第二,"时域求导"在频域对应乘以 j2πfj2\pi fj2πf,所以导数脉冲的谱会多一个 fff 的因子 ,导致 f=0f=0f=0 处谱为 0,并在某个非零频率附近形成峰值。如果把式 (2) 拆开看,会发现它就是"线性上升(∝f\propto f∝f)× 高斯衰减(∝e−f2\propto e^{-f^2}∝e−f2)",因此天然是一个"中频隆起、两端下降"的谱形。
3. 图 1 精读:同一族单周期脉冲如何随 fcf_cfc 改变"时域宽度/频域带宽"
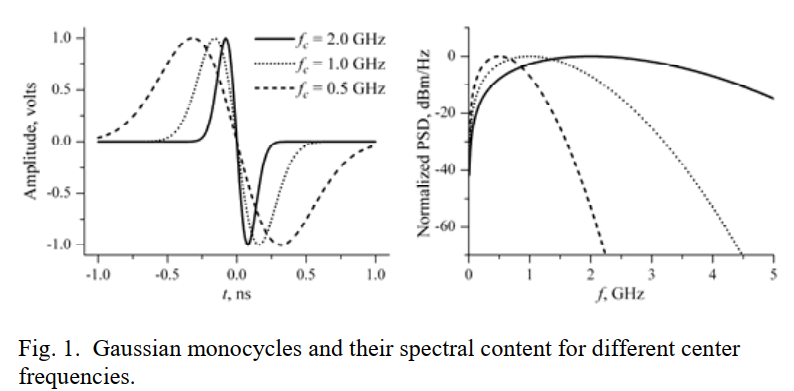
左侧(时域)横轴是 ttt(单位 ns),纵轴是幅度。我们能明显看到:当 fcf_cfc 较大时(图例里更高的 GHz 值),波形更"尖"、持续时间更短;当 fcf_cfc 较小时,波形更"宽"、摆动更慢。这正是 2πfct2\pi f_c t2πfct 控制时间尺度的直接后果。
右侧(频域)横轴是 fff(单位 GHz),纵轴是归一化 PSD。可以看到"谱峰"大致在某个与 fcf_cfc 同量级的位置,并且 fcf_cfc 越大,谱整体向高频移动,同时占用带宽更宽。更关键的是,谱在低频处接近 0(因为导数带来 fff 因子),这也是单周期脉冲区别于"普通高斯脉冲"的典型频谱指纹。
原文还提醒:单周期并不一定天然满足 FCC 频谱掩模,工程上要么合成更复杂的脉冲族,要么滤波整形,并且必须把收发天线的真实频响一起算进去,因为真正辐射出的电场波形会偏离理想单周期。
4. 统一发射信号模型式 (3):把帧、芯片、跳时、调制、扩频全部压到一行里
论文给出第 kkk 个用户 IR‑UWB 发射信号的"总括式"(式 (3)):
s(k)(t)=∑j=−∞∞ENs dj(k) β⌊j/Ns⌋(k) p (t−jTf−cj(k)Tc−δ α⌊j/Ns⌋(k)).(3) s^{(k)}(t)=\sum_{j=-\infty}^{\infty}\sqrt{\frac{E}{N_s}}\; d^{(k)}j\; \beta^{(k)}{\left\lfloor j/N_s\right\rfloor}\; p\!\left(t-jT_f-c^{(k)}jT_c-\delta\,\alpha^{(k)}{\left\lfloor j/N_s\right\rfloor}\right). \tag{3} s(k)(t)=j=−∞∑∞NsE dj(k)β⌊j/Ns⌋(k)p(t−jTf−cj(k)Tc−δα⌊j/Ns⌋(k)).(3)
要"读懂"这一行,最好的方式不是逐个符号背定义,而是把它拆成"时间格架 + 三种调制/码控":
首先,时间格架由 TfT_fTf 和 TcT_cTc 组成:一个符号持续时间 TTT 被分成若干 frame(帧),每帧长度 TfT_fTf;每帧再细分为 chip(芯片),每芯片长度 TcT_cTc。IR‑UWB 的脉冲宽度通常远小于 TfT_fTf,因此大部分时间"静默",只有很短的瞬间发一个脉冲,这就是文中说的"极低占空比"来源。
其次,帧内脉冲位置由 cj(k)Tcc^{(k)}_jT_ccj(k)Tc 决定。cj(k)c^{(k)}_jcj(k) 是伪随机正整数序列,告诉第 jjj 个脉冲落在当前帧的第几个 chip 上。这个机制叫 time hopping(跳时),其多用户意义是:不同用户的脉冲不至于总在同一 chip 上重合,避免"灾难性碰撞"。可以把它理解成:大家都在同样大小的时间格点上走,但每个人的"走位"由自己的伪随机码决定。
再往里一层,δ α\delta\,\alphaδα 代表 PPM(脉冲位置调制):在跳时决定的 chip 位置上,再做一个"与符号相关"的额外微移,δ\deltaδ 是调制指数(位置间隔),α\alphaα 是符号编号(例如二进制为 0/1)。因此 PPM 是"位置调制"通道。
与位置调制并列的是幅度/极性调制通道:β\betaβ 乘在脉冲前面,决定脉冲幅度或正负极性,从而可实现 PAM、OOK、BPSK 等。与之并行的 dj(k)d^{(k)}_jdj(k) 是 DS‑UWB(直扩)时用的二元双极性扩频码;文中之后为了讨论 TH‑UWB,会取 dj(k)=1d^{(k)}_j=1dj(k)=1。
最后,E/Ns\sqrt{E/N_s}E/Ns 是能量归一化:一个符号平均能量是 EEE,每个符号发 NsN_sNs 个脉冲,所以单脉冲能量应当是 E/NsE/N_sE/Ns,幅度就乘其平方根。这样调 NsN_sNs 时不会"偷偷改变"每比特能量定义,这对误码率公式非常关键。
5. PPM:正交与最优的差别不是"有没有移位",而是"相关性 Rp(δ)R_p(\delta)Rp(δ) 怎么进误码率"
5.1 图 2 精读:不同导数阶数改变自相关曲线,直接改变最优 δ\deltaδ
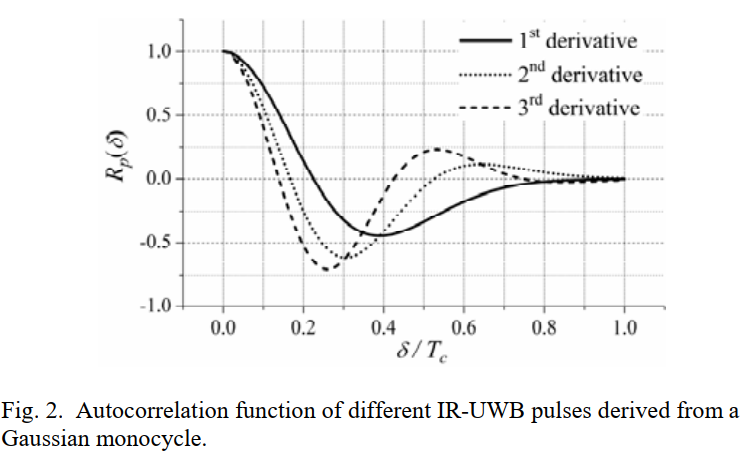
图 2 画的是不同 IR‑UWB 脉冲(由高斯单周期进一步求导得到的一阶、二阶、三阶导数波形)的归一化自相关函数 Rp(δ)R_p(\delta)Rp(δ),横轴是 δ/Tc\delta/T_cδ/Tc,纵轴是 Rp(δ)R_p(\delta)Rp(δ)。这张图的"可读信息"非常具体:
-
当用"传统单周期"时,自相关在 δ≈0.4Tc\delta\approx 0.4T_cδ≈0.4Tc 附近出现更深的负谷(意味着两种 PPM 波形相互更不相似,欧氏距离更大),所以最优分离 δopt\delta_{\text{opt}}δopt 大约落在 0.4 倍芯片宽度。
-
当用"高阶导数脉冲"(尤其三阶)时,自相关曲线的谷底位置前移到 δ≈0.25Tc\delta\approx 0.25T_cδ≈0.25Tc。论文的工程解释是:δopt\delta_{\text{opt}}δopt 变小意味着在同样的芯片时间预算内可以容纳更高的符号率,或者在同样符号率下用更紧凑的时间位移获得更好的功率效率。
5.2 式 (4) 的推导主线:误码率由"波形差的能量"决定,而波形差的能量由自相关决定
论文给出单用户 AWGN 下最优二进制 TH‑PPM 的平均符号误差率(式 (4)):
Pe=12erfc (Eb2N0[Rp(0)−Rp(δopt)]).(4) P_e=\frac12\operatorname{erfc}\!\left( \sqrt{\frac{E_b}{2N_0}\left[R_p(0)-R_p(\delta_{\text{opt}})\right]} \right). \tag{4} Pe=21erfc(2N0Eb[Rp(0)−Rp(δopt)] ).(4)
这里 EbE_bEb 是每比特能量(文中强调 Eb=Ns×E_b=N_s\timesEb=Ns× 单脉冲能量),N0N_0N0 是噪声双边功率谱密度。式 (4) 的灵魂在括号里: Rp(0)−Rp(δ) \,R_p(0)-R_p(\delta)\,Rp(0)−Rp(δ)。因为 Rp(0)=1R_p(0)=1Rp(0)=1,所以它其实是 1−Rp(δ)1-R_p(\delta)1−Rp(δ),也就是"两个波形的相似度越低,误码率越好"。
为什么"相似度"会这样进入?因为二元最优检测在 AWGN 下只看两信号的欧氏距离。令两种 PPM 波形为
s0(t)=Eb p(t),s1(t)=Eb p(t−δ), s_0(t)=\sqrt{E_b}\,p(t),\qquad s_1(t)=\sqrt{E_b}\,p(t-\delta), s0(t)=Eb p(t),s1(t)=Eb p(t−δ),
则差波形能量为
∥s0−s1∥2=∥s0∥2+∥s1∥2−2⟨s0,s1⟩=2Eb−2EbRp(δ)=2Eb[1−Rp(δ)]. \|s_0-s_1\|^2 =\|s_0\|^2+\|s_1\|^2-2\langle s_0,s_1\rangle =2E_b-2E_bR_p(\delta) =2E_b\bigl[1-R_p(\delta)\bigr]. ∥s0−s1∥2=∥s0∥2+∥s1∥2−2⟨s0,s1⟩=2Eb−2EbRp(δ)=2Eb[1−Rp(δ)].
而二元 ML 检测的错误概率满足
Pe=Q (∥s0−s1∥22N0)=12 erfc (∥s0−s1∥24N0). P_e=Q\!\left(\sqrt{\frac{\|s_0-s_1\|^2}{2N_0}}\right) =\frac12\,\operatorname{erfc}\!\left( \sqrt{\frac{\|s_0-s_1\|^2}{4N_0}} \right). Pe=Q 2N0∥s0−s1∥2 =21erfc 4N0∥s0−s1∥2 .
把 ∥s0−s1∥2=2Eb[1−Rp(δ)]\|s_0-s_1\|^2=2E_b[1-R_p(\delta)]∥s0−s1∥2=2Eb[1−Rp(δ)] 代进去,就得到式 (4)。我们会看到:所谓"正交 PPM"只不过是把 δ=Tc\delta=T_cδ=Tc 选到让两脉冲不重叠,近似 Rp(δ)=0R_p(\delta)=0Rp(δ)=0,于是 Rp(0)−Rp(δ)=1R_p(0)-R_p(\delta)=1Rp(0)−Rp(δ)=1,性能退化为经典的二元正交信号误码率。
6. BPSK / 双正交 / PAM / OOK / PSM:式 (3) 如何一键退化成熟悉调制,以及式 (5)(6) 的"几何本质"
论文接着把式 (3) 特化成几种典型体制,并把 AWGN 单用户误码/误符号率直接引用为通信理论的标准结果。
当取 δ=0\delta=0δ=0 且 β=±1\beta=\pm 1β=±1 时,信号只是在每个符号间隔把脉冲翻相或不翻相,因此是 TH‑BPSK。它在 AWGN 里等价于反相(antipodal)二元信号,距离最大,错误概率就是大家熟悉的 BPSK 结论(文中不再重写公式,而是引用教材推导)。
当用 M/2M/2M/2 个正交波形再加上它们的负号,就得到 MMM 元双正交(bi‑orthogonal)。论文给了 MMM 元双正交的平均符号误差率积分形式(式 (5)),并指出 E=Eblog2ME=E_b\log_2ME=Eblog2M。这类积分式本质是在算"正确维度上的高斯偏移变量"与"其余 M/2−1M/2-1M/2−1 个维度噪声变量的最大值"之间的比较概率,等价于多维高斯统计量的分布计算。
当取 δ=0\delta=0δ=0 且 β∈{ai}\beta\in\{a_i\}β∈{ai} 为 MMM 个幅度电平,就得到 TH‑PAM。论文给出 MMM 元 PAM 的平均符号误差率(式 (6)):
Pe=M−1Merfc (3E(M2−1)N0),E=Eblog2M.(6) P_e=\frac{M-1}{M}\operatorname{erfc}\!\left( \sqrt{\frac{3E}{(M^2-1)N_0}} \right), \qquad E=E_b\log_2M. \tag{6} Pe=MM−1erfc((M2−1)N03E ),E=Eblog2M.(6)
这跟窄带 PAM 的形式完全一致;IR‑UWB 的差别只是"一个符号能量 EEE"来自 NsN_sNs 个脉冲能量相加。OOK 则是 PAM 的特例:β∈{0,a}\beta\in\{0,a\}β∈{0,a}。PSM(脉冲形状调制)是把 p(t)p(t)p(t) 换成一组 pi(t)p_i(t)pi(t),其误差率强依赖波形集合的互相关,因此论文明确说"不可能写一个统一的误差率表达式"。
7. 大尺度信道:从自由空间 (7)(8) 到两径临界距离 (9),再到对数距离 + 阴影 (10)--(14)
7.1 自由空间路径损耗式 (7)(8):就是 Friis 公式取对数
作者给出不计天线增益时的自由空间路径损耗(dB):
L(d)=10logPTPR=−10log(λ216π2d2) dB,(7) L(d)=10\log\frac{P_T}{P_R} =-10\log\left(\frac{\lambda^2}{16\pi^2 d^2}\right)\ \text{dB}, \tag{7} L(d)=10logPRPT=−10log(16π2d2λ2) dB,(7)
计入天线增益 GT,GRG_T,G_RGT,GR 时:
L(d)=−10log(GTGRλ216π2d2) dB.(8) L(d)=-10\log\left(\frac{G_TG_R\lambda^2}{16\pi^2 d^2}\right)\ \text{dB}. \tag{8} L(d)=−10log(16π2d2GTGRλ2) dB.(8)
这两式等价于 Friis
PR=PTGTGR(λ4πd)2, P_R=P_TG_TG_R\left(\frac{\lambda}{4\pi d}\right)^2, PR=PTGTGR(4πdλ)2,
只不过把比值取对数写成 dB。论文借此强调:自由空间里 PR∝d−2P_R\propto d^{-2}PR∝d−2,对应路径损耗指数 n=2n=2n=2;实际近地传播中 nnn 往往大于 2。
7.2 两径模型与临界距离式 (9):为什么会从 d−2d^{-2}d−2 变成 d−4d^{-4}d−4
在引入对数距离模型前,先用两径模型做"直觉铺垫",并给出临界距离
dc=4hThRλ.(9) d_c=\frac{4h_T h_R}{\lambda}. \tag{9} dc=λ4hThR.(9)
这条式子出现的本质原因是:远距离时直达波与地反射波的相位差随距离变化更慢,且两路叠加在平均意义上呈现更快的功率衰减;在经典两径推导里,远区叠加结果导致 PR∝d−4P_R\propto d^{-4}PR∝d−4。论文用图 3 把这种"近区干涉凹陷 + 远区双斜率"画了出来。
7.3 图 3 精读:左边一堆深凹是相消干涉,右边斜率变陡是两径远区 d−4d^{-4}d−4
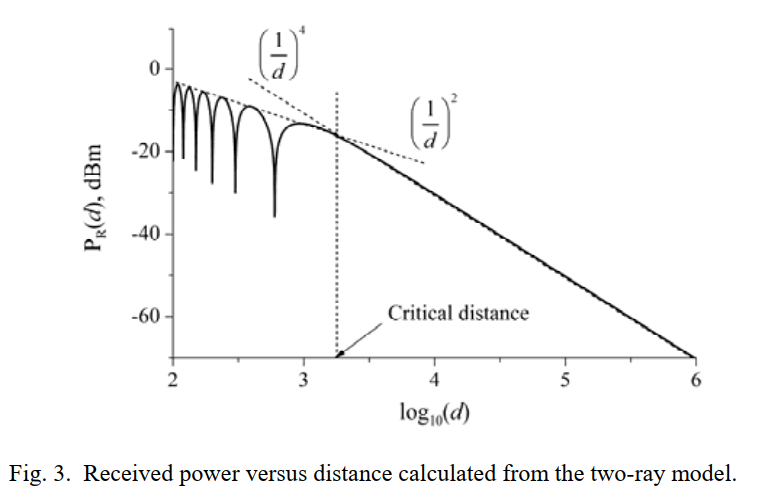
图 3 横轴是 log10(d)\log_{10}(d)log10(d),纵轴是接收功率 PR(d)P_R(d)PR(d)(dBm)。图里标出了临界距离(critical distance)。在临界距离左侧,曲线有很多"深凹",这正是直达与反射相位差造成的周期性相消/相长干涉;但平均趋势(图中虚线)仍接近 d−2d^{-2}d−2。
过了临界距离,深凹逐渐消失,平均趋势变为更陡的 d−4d^{-4}d−4 斜率(图中另一条虚线)。如果我们要用一个简单的"单斜率路径损耗"去拟合真实数据,最好在"超过某个距离后"才做回归会更稳。
7.4 对数距离模型式 (10)(11):把幂律写成 dB 里的直线,再加一个高斯扰动
论文把大尺度衰落拆成"距离决定的面积平均项 + 障碍物造成的局部平均偏移"。若在参考距离 d0d_0d0 处定义面积平均损耗 L‾(d0)\overline{L}(d_0)L(d0),则
L‾(d)=L‾(d0)+10nlog10(dd0) dB.(10) \overline{L}(d)=\overline{L}(d_0)+10n\log_{10}\left(\frac{d}{d_0}\right)\ \text{dB}. \tag{10} L(d)=L(d0)+10nlog10(d0d) dB.(10)
再加上阴影(lognormal shadowing)随机项 XσX_\sigmaXσ:
L(d)=L‾(d0)+10nlog10(dd0)+Xσ dB,(11) L(d)=\overline{L}(d_0)+10n\log_{10}\left(\frac{d}{d_0}\right)+X_\sigma\ \text{dB}, \tag{11} L(d)=L(d0)+10nlog10(d0d)+Xσ dB,(11)
其中 XσX_\sigmaXσ 在 dB 域近似高斯,标准差为 σ\sigmaσ。
7.5 图 4 精读:固定距离绕圈走,平均不变,局部上下抖动
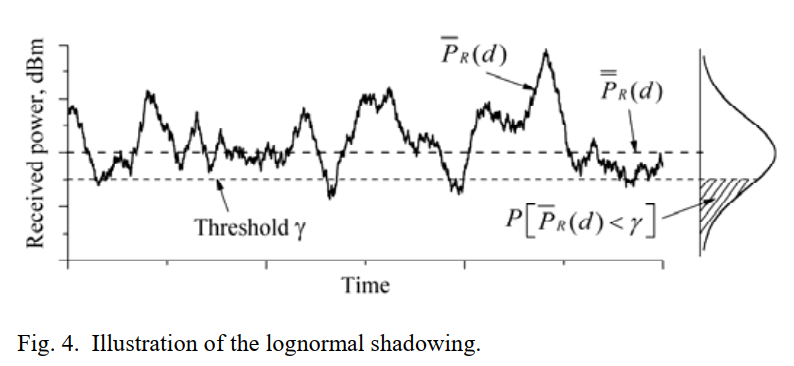
图 4 左侧画了一条随时间变化的"局部平均接收功率轨迹",可以把它理解为:接收机保持与发射机距离恒定(比如绕着发射机转圈),由于身边的障碍物配置不断变化,局部平均功率会围绕面积平均功率上下波动。图中画了一条阈值线 γ\gammaγ,并在一段时间里出现"低于阈值"的区间。
图 4 右侧画的是 dB 域高斯概率密度:横轴是功率,中心在 PR(d)‾\overline{P_R(d)}PR(d),散布由 σ\sigmaσ 决定。这样就能算出 Pr{PR(d)>γ}\Pr\{P_R(d)>\gamma\}Pr{PR(d)>γ} 或 Pr{PR(d)<γ}\Pr\{P_R(d)<\gamma\}Pr{PR(d)<γ}。整个图像表达的是:对数距离模型未必能预测某个具体点的功率,但它能给出"统计置信度"。
7.6 参数估计式 (12)(13):MSE 最小化对应拟合 nnn,残差方差对应 σ2\sigma^2σ2
论文用均方误差来估计 nnn:
J(n)=1K∑k=0K−1[Pk−Pk(n)]2,(12) J(n)=\frac{1}{K}\sum_{k=0}^{K-1}\left[P_k-P_k(n)\right]^2, \tag{12} J(n)=K1k=0∑K−1[Pk−Pk(n)]2,(12)
并指出当 nnn 取使 MSE 最小的估计值时,阴影标准差可取
σ=J(n)∣n:minMSE dB.(13) \sigma=\sqrt{J(n)}\Big|_{n:\min\text{MSE}}\ \text{dB}. \tag{13} σ=J(n) n:minMSE dB.(13)
其统计直觉非常直接:模型拟合后的残差就是阴影项样本,残差的样本方差就是 σ2\sigma^2σ2 的估计。
7.7 覆盖"面积比例"式 (14) 与图 5:从点概率扩展到"整个圆盘里多少面积满足门限"
作者进一步问了一个更像运营指标的问题:不止要知道"边界圆周上"超过阈值的概率,还要知道"整个半径 ddd 的圆形覆盖区里,有多少面积比例的接收功率能超过阈值"。给出闭式表达(式 (14)):
F(γ)=12[erfc(a)+exp(1−2abb2)erfc (1−abb)],(14) F(\gamma)=\frac12\left[ \operatorname{erfc}(a)+\exp\left(\frac{1-2ab}{b^2}\right)\operatorname{erfc}\!\left(\frac{1-ab}{b}\right) \right], \tag{14} F(γ)=21[erfc(a)+exp(b21−2ab)erfc(b1−ab)],(14)
其中
a=γ−PR(d)‾σ2,b=10nlog10(e)σ2. a=\frac{\gamma-\overline{P_R(d)}}{\sigma\sqrt2}, \qquad b=\frac{10n\log_{10}(e)}{\sigma\sqrt2}. a=σ2 γ−PR(d),b=σ2 10nlog10(e).
这实际上是把"半径从 0 到 ddd"的点概率按面积权重 2r/dr2r/dr2r/dr 做积分平均后得到的解析形式(完整推导在附录里)。
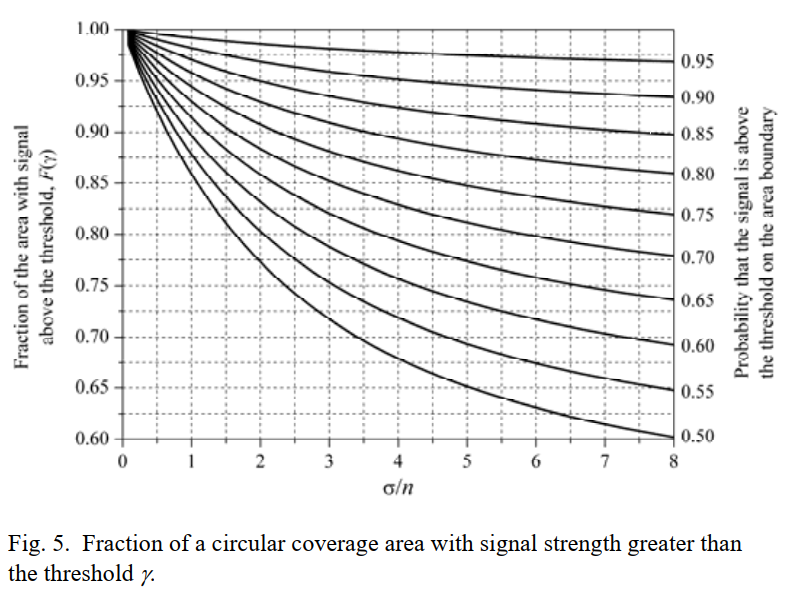
其中横轴是 σ/n\sigma/nσ/n,右侧纵轴是圆周边界处"超过门限"的概率(也就是 Pr{PR(d)>γ}\Pr\{P_R(d)>\gamma\}Pr{PR(d)>γ}),左侧纵轴是圆盘内的"面积比例"。图里一组曲线从 0.95、0.90...一直往下标注,代表不同的边界点概率。可以按原文描述的用法:先算 σ/n\sigma/nσ/n,再找到对应边界概率曲线,往左读出面积比例。
8. 小尺度信道:Saleh--Valenzuela(SV)模型把"簇 + 簇内射线"写成可仿真的随机生成器
论文在 III‑E 用 SV 模型作为 IR‑UWB 室内小尺度信道的代表模型(或其改型),并给出 tapped delay line 形式的冲激响应(式 (15)):
h(t)=∑l=0∞∑k=0∞αklejθkl δ(t−Tl−τkl).(15) h(t)=\sum_{l=0}^{\infty}\sum_{k=0}^{\infty}\alpha_{kl}e^{j\theta_{kl}}\;\delta(t-T_l-\tau_{kl}). \tag{15} h(t)=l=0∑∞k=0∑∞αklejθklδ(t−Tl−τkl).(15)
这里 TlT_lTl 是第 lll 个簇(cluster)的到达时刻,τkl\tau_{kl}τkl 是簇内第 kkk 条射线(ray)相对簇起点的延迟;αkl\alpha_{kl}αkl 与 θkl\theta_{kl}θkl 分别是幅度与相位。SV 模型用两个"泊松到达过程"来刻画簇与簇内射线的到达:簇间隔的条件密度为指数分布(式 (16)),簇内射线间隔同理(式 (19))。
随后论文把大尺度路径损耗接进来,用参考距离 d0=1d_0=1d0=1 m 给出线性尺度路径损耗幂律(式 (17)):
L‾(d)=L‾(1m) dn,(17) \overline{L}(d)=\overline{L}(1\text{m})\,d^n, \tag{17} L(d)=L(1m)dn,(17)
并用它标定第一簇第一射线平均功率(式 (18)):
E[α002]=(γλ)−1/(L‾(1m) dn),(18) E[\alpha_{00}^2]=(\gamma\lambda)^{-1}\Big/\left(\overline{L}(1\text{m})\,d^n\right), \tag{18} E[α002]=(γλ)−1/(L(1m)dn),(18)
其中 λ\lambdaλ 是簇内射线到达率,γ\gammaγ 是簇内射线功率指数衰减时间常数;簇级功率衰减时间常数为 Γ\GammaΓ。其后,SV 模型规定每条射线的均方值按"簇延迟 + 簇内延迟"双指数衰减(式 (21)):
E[αkl2]=E[α002]exp(−TlΓ)exp(−τklγ).(21) E[\alpha_{kl}^2]=E[\alpha_{00}^2]\exp\left(-\frac{T_l}{\Gamma}\right)\exp\left(-\frac{\tau_{kl}}{\gamma}\right). \tag{21} E[αkl2]=E[α002]exp(−ΓTl)exp(−γτkl).(21)
幅度 αkl\alpha_{kl}αkl 取瑞利分布(式 (20)),相位 θkl\theta_{kl}θkl 取 000 到 2π2\pi2π 均匀分布(式 (22)),并给出用两个独立高斯变量生成瑞利幅度与相位的公式(式 (23))。
图 6 精读:簇与簇内射线的"双指数衰减"在图上就是两层包络
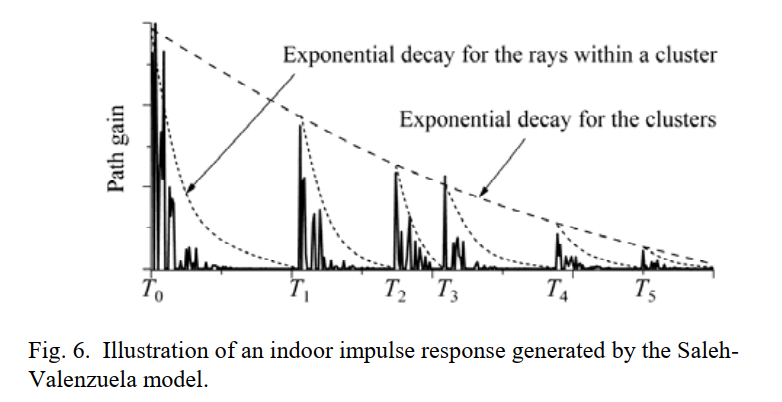
图 6 画了一个 SV 生成的室内冲激响应示意。横轴是延迟(图上标了 T0,T1,...T_0,T_1,\dotsT0,T1,... 的簇到达时刻),纵轴是幅度。可以看到:每个簇内部有很多尖峰(射线),尖峰的包络随簇内时间 τ\tauτ 指数下降;不同簇之间的整体峰值也指数下降。图上两条标注"Exponential decay..."的包络箭头,基本就是式 (21) 两个指数因子的可视化。
9. 接收与时间反转(Time Reversal):把多径从"需要很长 RAKE/均衡器"变成"自相关峰值聚焦"
论文在 IV 里先讲一个 IR‑UWB 接收的根本事实:单个脉冲能量很低,所以常用 NsN_sNs 个脉冲/符号并用多相关器累加;在多径信道里可以做 RAKE(尤其是 UWB 的高时间分辨率让"路径可分辨"更多),但代价是 tap 数可能很大;最优 MLSE 又太复杂;还有 transmitted reference 等折中。原文把这些作为"常见背景"快速带过,然后重点讲时间反转。
时间反转的核心操作一句话就够:发射端用预滤波器,其冲激响应等于信道冲激响应的"共轭 + 时间反转" ,即 h∗(r,−τ)h^*(r,-\tau)h∗(r,−τ)。于是"预滤波器与信道串联"的复合响应变成
hcomp(τ)=h∗(r,−τ)∗h(r,τ), h_{\text{comp}}(\tau)=h^*(r,-\tau)*h(r,\tau), hcomp(τ)=h∗(r,−τ)∗h(r,τ),
而"信号与其共轭时间反转的卷积"在形状上等价于自相关,因此 hcomph_{\text{comp}}hcomp 会出现显著的相关峰,表现为能量集中,从而降低接收端能量收集/均衡的复杂度(代价是发射端要估计 CIR 并构造预滤波器)。
图 7 精读:时间反转把复杂度从接收端搬到发射端
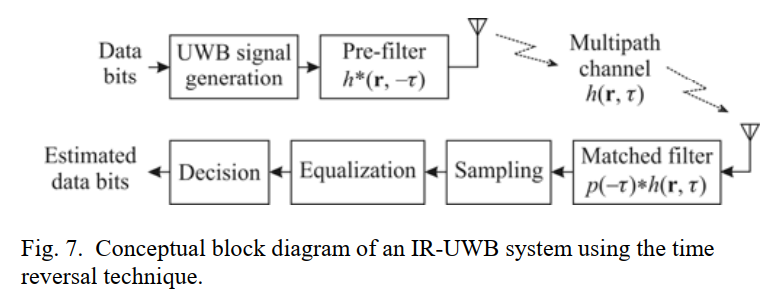
图 7 的框图从左到右是:数据比特 → UWB 信号生成(产生 p(t)p(t)p(t) 序列)→ 预滤波器 h∗(r,−τ)h^*(r,-\tau)h∗(r,−τ) → 多径信道 h(r,τ)h(r,\tau)h(r,τ) → 接收端匹配滤波器(冲激响应写成 p(−τ)∗h(r,τ)p(-\tau)*h(r,\tau)p(−τ)∗h(r,τ),说明它匹配的是"实际通过信道后的脉冲形状")→ 抽样 → 均衡(消残余 ISI)→ 判决。图中把位置变量 rrr 写进 h(r,τ)h(r,\tau)h(r,τ) 是为了强调:室内 UWB 信道对位置极敏感,这也与后文"空间聚焦、降低多用户干扰"的讨论相呼应。
图 8 精读:原始 CIR 能量分散,复合响应出现尖峰聚焦
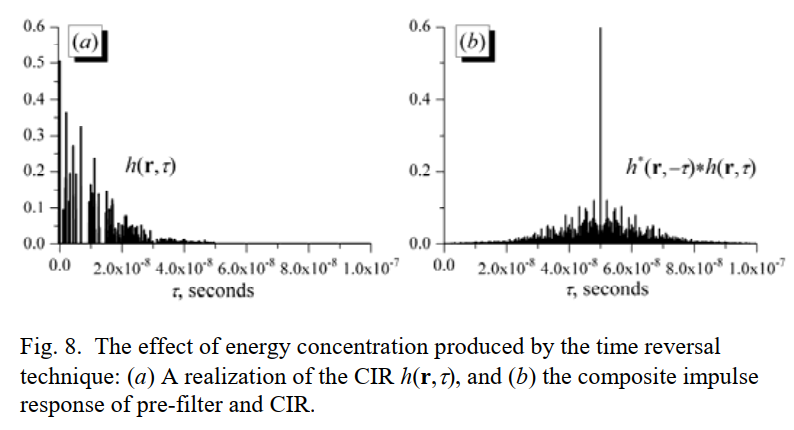
图 8(a) 是一个假想的室内 CIR ∣h(r,τ)∣|h(r,\tau)|∣h(r,τ)∣:很多分散的多径尖峰,时间扩展较长;图 8(b) 是 h∗(r,−τ)∗h(r,τ)h^*(r,-\tau)*h(r,\tau)h∗(r,−τ)∗h(r,τ)(自相关形状),我们可以明显看到一个很突出的峰值。论文给出的解释是:在丰富散射环境里,多径分量高度不相关,非零延迟处交叉项相互抵消,而零延迟处的 ∣αi∣2|\alpha_i|^2∣αi∣2 项同相叠加,于是峰值显著。图 8(b) 也提醒一个细节:复合响应"长度可能更长",但"可用能量在少数采样点更集中",因此接收端可以用更短的均衡器或更少的 RAKE tap 抓住主要能量。
10. 应用部分:IEEE 802.15.4a、认知无线电、成像/测距、车载雷达的共同底层优势
原文最后把应用分成几类:IEEE 802.15.4a 把 IR‑UWB 纳入 PHY 以增强定位/测距;认知无线电场景强调 IR‑UWB 的低功率谱密度与可自适应性;成像(GPR、穿墙、医学)与测量系统依赖 UWB 的高时间分辨率(回波分辨能力);车载雷达用于防撞/泊车辅助等。可以发现这些应用虽然表面不同,但"共同的底层好处"高度一致:极宽带宽带来的高时间分辨率,使得"分辨多径/回波"和"精确测距定位"变得可行。
附录
附录 A:从"高斯脉冲"推到"高斯单周期"式 (1),再推到 PSD 形状式 (2)
A.1 选一个方便推导的高斯原型
令一个归一化高斯原型为
g(t)=exp (−t22σt2). g(t)=\exp\!\left(-\frac{t^2}{2\sigma_t^2}\right). g(t)=exp(−2σt2t2).
其导数为
g′(t)=−tσt2exp (−t22σt2), g'(t)= -\frac{t}{\sigma_t^2}\exp\!\left(-\frac{t^2}{2\sigma_t^2}\right), g′(t)=−σt2texp(−2σt2t2),
这已经具有"单周期"形态:乘了一个 ttt 使其在 0 处过零、左右异号。
把 σt\sigma_tσt 写成 fcf_cfc 的形式:令
σt=12πfc. \sigma_t=\frac{1}{2\pi f_c}. σt=2πfc1.
则
g′(t)=−(2πfc)2texp (−(2πfct)22). g'(t)=-(2\pi f_c)^2 t \exp\!\left(-\frac{(2\pi f_c t)^2}{2}\right). g′(t)=−(2πfc)2texp(−2(2πfct)2).
这与原文式 (1) 的形状一致:都是 t⋅e−(2πfct)2/2t\cdot e^{-(2\pi f_c t)^2/2}t⋅e−(2πfct)2/2 乘上一个常数。原文在指数里额外出现 exp{1/2}\exp\{1/2\}exp{1/2} 的归一化常数(把峰值或能量做了某种标定),这些常数不改变"波形族"的核心结构与频谱形态,只改变幅度标度,因此并不影响后续"相关性/距离/误码率"推导的结论结构。
由此也能解释原文的经验关系 fc≈1/τf_c\approx 1/\taufc≈1/τ:因为 σt∼1/fc\sigma_t\sim 1/f_cσt∼1/fc,而脉冲"显著非零"的时间跨度与 σt\sigma_tσt 同量级。
A.2 导数为什么让低频 PSD 变成 0:频域乘 j2πfj2\pi fj2πf
设 g(t)g(t)g(t) 的傅里叶变换为 G(f)G(f)G(f)。在采用 e−j2πfte^{-j2\pi ft}e−j2πft 约定时,
F{g′(t)}=j2πf G(f). \mathcal{F}\{g'(t)\}=j2\pi f\,G(f). F{g′(t)}=j2πfG(f).
因此导数脉冲的功率谱密度满足
∣F{g′(t)}∣2=(2πf)2 ∣G(f)∣2, | \mathcal{F}\{g'(t)\}|^2 = (2\pi f)^2\,|G(f)|^2, ∣F{g′(t)}∣2=(2πf)2∣G(f)∣2,
这就强制了 f=0f=0f=0 处为 0(因为乘了 f2f^2f2)。
另一方面,高斯的傅里叶变换仍是高斯:
g(t)=e−t2/(2σt2)⟹G(f)=σt2π e−2π2σt2f2. g(t)=e^{-t^2/(2\sigma_t^2)} \quad \Longrightarrow\quad G(f)=\sigma_t\sqrt{2\pi}\,e^{-2\pi^2\sigma_t^2 f^2}. g(t)=e−t2/(2σt2)⟹G(f)=σt2π e−2π2σt2f2.
于是
∣G(f)∣2∝e−4π2σt2f2. |G(f)|^2\propto e^{-4\pi^2\sigma_t^2 f^2}. ∣G(f)∣2∝e−4π2σt2f2.
带入 σt=1/(2πfc)\sigma_t=1/(2\pi f_c)σt=1/(2πfc),得到
∣G(f)∣2∝e−(f/fc)2. |G(f)|^2\propto e^{-(f/f_c)^2}. ∣G(f)∣2∝e−(f/fc)2.
再乘上导数带来的 f2f^2f2 因子,你就得到一种典型形状:
∣F{g′(t)}∣2∝f2 e−(f/fc)2. | \mathcal{F}\{g'(t)\}|^2 \propto f^2\,e^{-(f/f_c)^2}. ∣F{g′(t)}∣2∝f2e−(f/fc)2.
原文式 (2) 写的是归一化后的 PSD,形式上等价于
P(f)∝(ffc)exp (−12(ffc)2), P(f)\propto \left(\frac{f}{f_c}\right)\exp\!\left(-\frac12\left(\frac{f}{f_c}\right)^2\right), P(f)∝(fcf)exp(−21(fcf)2),
差别主要来自归一化常数与具体原型定义(是高斯本体还是电场/电压对应的导数阶数)。无论采用哪一种常数约定,关键物理结果一致:导数把低频压成 0,高斯包络把高频指数压下,中间出现峰值。这正是图 1 右侧曲线的核心形状来源。
附录 B:式 (4) 的检测论推导(从相关器输出到 erfc\operatorname{erfc}erfc)
考虑二元 PPM,忽略多用户与多径,AWGN 下接收信号为
r(t)=si(t)+n(t),i∈{0,1}, r(t)=s_i(t)+n(t),\qquad i\in\{0,1\}, r(t)=si(t)+n(t),i∈{0,1},
其中 n(t)n(t)n(t) 为双边 PSD 为 N0/2N_0/2N0/2 的白高斯噪声。
令两种波形(等能量)为
s0(t)=Eb p(t),s1(t)=Eb p(t−δ). s_0(t)=\sqrt{E_b}\,p(t),\qquad s_1(t)=\sqrt{E_b}\,p(t-\delta). s0(t)=Eb p(t),s1(t)=Eb p(t−δ).
最优 ML 判决可用"差相关器"实现:比较
Λ=⟨r,s0⟩−⟨r,s1⟩. \Lambda=\langle r,s_0\rangle-\langle r,s_1\rangle. Λ=⟨r,s0⟩−⟨r,s1⟩.
若 Λ>0\Lambda>0Λ>0 判 s0s_0s0,否则判 s1s_1s1。
在发送 s0s_0s0 的条件下,
Λ=⟨s0+n,s0⟩−⟨s0+n,s1⟩=⟨s0,s0⟩−⟨s0,s1⟩+⟨n,s0−s1⟩. \Lambda =\langle s_0+n,s_0\rangle-\langle s_0+n,s_1\rangle =\langle s_0,s_0\rangle-\langle s_0,s_1\rangle+\langle n,s_0-s_1\rangle. Λ=⟨s0+n,s0⟩−⟨s0+n,s1⟩=⟨s0,s0⟩−⟨s0,s1⟩+⟨n,s0−s1⟩.
第一项是能量 EbE_bEb。第二项是互相关:
⟨s0,s1⟩=Eb Rp(δ), \langle s_0,s_1\rangle =E_b\,R_p(\delta), ⟨s0,s1⟩=EbRp(δ),
其中
Rp(δ)=∫p(t)p(t−δ) dt∫p2(t) dt, R_p(\delta)=\frac{\int p(t)p(t-\delta)\,dt}{\int p^2(t)\,dt}, Rp(δ)=∫p2(t)dt∫p(t)p(t−δ)dt,
这正是原文所说"相对脉冲能量归一化的自相关函数"。
因此
Λ=Eb[1−Rp(δ)]+Z, \Lambda = E_b\bigl[1-R_p(\delta)\bigr] + Z, Λ=Eb[1−Rp(δ)]+Z,
其中噪声项
Z=⟨n,s0−s1⟩ Z=\langle n,s_0-s_1\rangle Z=⟨n,s0−s1⟩
是高斯随机变量,均值 0,方差为
Var(Z)=N02 ∥s0−s1∥2, \operatorname{Var}(Z) =\frac{N_0}{2}\,\|s_0-s_1\|^2, Var(Z)=2N0∥s0−s1∥2,
这是 AWGN 内积噪声的标准结论。又因为
∥s0−s1∥2=2Eb[1−Rp(δ)], \|s_0-s_1\|^2=2E_b\bigl[1-R_p(\delta)\bigr], ∥s0−s1∥2=2Eb[1−Rp(δ)],
所以
Var(Z)=N02⋅2Eb[1−Rp(δ)]=N0Eb[1−Rp(δ)]. \operatorname{Var}(Z)=\frac{N_0}{2}\cdot 2E_b[1-R_p(\delta)] =N_0E_b[1-R_p(\delta)]. Var(Z)=2N0⋅2Eb[1−Rp(δ)]=N0Eb[1−Rp(δ)].
错误事件(发送 s0s_0s0 却判 s1s_1s1)是 Λ<0\Lambda<0Λ<0,即
Z<−Eb[1−Rp(δ)]. Z< -E_b[1-R_p(\delta)]. Z<−Eb[1−Rp(δ)].
把 ZZZ 标准化得到
Pe=Q (Eb[1−Rp(δ)]N0Eb[1−Rp(δ)])=Q (EbN0[1−Rp(δ)]). P_e =Q\!\left(\frac{E_b[1-R_p(\delta)]}{\sqrt{N_0E_b[1-R_p(\delta)]}}\right) =Q\!\left(\sqrt{\frac{E_b}{N_0}[1-R_p(\delta)]}\right). Pe=Q(N0Eb[1−Rp(δ)] Eb[1−Rp(δ)])=Q(N0Eb[1−Rp(δ)] ).
利用 Q(x)=12erfc(x/2)Q(x)=\tfrac12\operatorname{erfc}(x/\sqrt2)Q(x)=21erfc(x/2 ),得
Pe=12erfc (Eb2N0[1−Rp(δ)])=12erfc (Eb2N0[Rp(0)−Rp(δ)]), P_e =\frac12\operatorname{erfc}\!\left( \sqrt{\frac{E_b}{2N_0}[1-R_p(\delta)]} \right) =\frac12\operatorname{erfc}\!\left( \sqrt{\frac{E_b}{2N_0}[R_p(0)-R_p(\delta)]} \right), Pe=21erfc(2N0Eb[1−Rp(δ)] )=21erfc(2N0Eb[Rp(0)−Rp(δ)] ),
即原文式 (4)。
附录 C:两径模型临界距离式 (9) 的一条常见推导路径
两径模型里,接收场是直达与地反射两路叠加。设发射天线高度 hTh_ThT,接收天线高度 hRh_RhR,水平距离 ddd。
直达路径长度
ℓ1=d2+(hT−hR)2, \ell_1=\sqrt{d^2+(h_T-h_R)^2}, ℓ1=d2+(hT−hR)2 ,
反射路径长度可用"镜像法":把发射天线关于地面镜像到高度 −hT-h_T−hT,则反射路等价于从镜像点到接收点的直线距离:
ℓ2=d2+(hT+hR)2. \ell_2=\sqrt{d^2+(h_T+h_R)^2}. ℓ2=d2+(hT+hR)2 .
当 ddd 远大于高度时,可用二项式展开
d2+a2=d1+(a/d)2≈d(1+a22d2)=d+a22d. \sqrt{d^2+a^2}=d\sqrt{1+(a/d)^2}\approx d\left(1+\frac{a^2}{2d^2}\right) =d+\frac{a^2}{2d}. d2+a2 =d1+(a/d)2 ≈d(1+2d2a2)=d+2da2.
于是
ℓ1≈d+(hT−hR)22d,ℓ2≈d+(hT+hR)22d. \ell_1\approx d+\frac{(h_T-h_R)^2}{2d},\qquad \ell_2\approx d+\frac{(h_T+h_R)^2}{2d}. ℓ1≈d+2d(hT−hR)2,ℓ2≈d+2d(hT+hR)2.
路径差
Δℓ=ℓ2−ℓ1≈(hT+hR)2−(hT−hR)22d=4hThR2d=2hThRd. \Delta \ell=\ell_2-\ell_1 \approx \frac{(h_T+h_R)^2-(h_T-h_R)^2}{2d} =\frac{4h_T h_R}{2d} =\frac{2h_T h_R}{d}. Δℓ=ℓ2−ℓ1≈2d(hT+hR)2−(hT−hR)2=2d4hThR=d2hThR.
当路径差小于波长量级时,相位差变化快、干涉凹陷明显;当距离更大、相位差变化更慢且反射系数接近 −1 时,叠加后的场幅度近似与 1/d21/d^21/d2 成比例,从而功率近似 1/d41/d^41/d4。临界距离通常取"路径差等于半波长或一波长的某个常数倍"的量级判据。若取
Δℓ≈λ2, \Delta \ell \approx \frac{\lambda}{2}, Δℓ≈2λ,
则
2hThRdc≈λ2⇒dc≈4hThRλ, \frac{2h_T h_R}{d_c}\approx \frac{\lambda}{2} \quad\Rightarrow\quad d_c\approx \frac{4h_T h_R}{\lambda}, dc2hThR≈2λ⇒dc≈λ4hThR,
即原文式 (9)。不同教材在常数因子上可能因"判据选 λ/2\lambda/2λ/2 还是 λ\lambdaλ"略有差异,但数量级与结构一致:dc∝hThR/λd_c\propto h_T h_R/\lambdadc∝hThR/λ。
附录 D:覆盖面积比例式 (14) 的推导(从面积积分到 erfc 闭式)
目标是求半径为 ddd 的圆盘内,接收功率超过阈值 γ\gammaγ 的面积比例 F(γ)F(\gamma)F(γ)。
D.1 点概率:半径 rrr 处超过阈值的概率
对数距离 + 阴影模型在 dB 域可写成
PR(r)=PR(r)‾+Xσ,Xσ∼N(0,σ2). P_R(r)=\overline{P_R(r)}+X_\sigma,\qquad X_\sigma\sim\mathcal{N}(0,\sigma^2). PR(r)=PR(r)+Xσ,Xσ∼N(0,σ2).
若以边界 r=dr=dr=d 的面积平均功率 PR(d)‾\overline{P_R(d)}PR(d) 为参考,则
PR(r)‾=PR(d)‾+10nlog10 (dr). \overline{P_R(r)} =\overline{P_R(d)}+10n\log_{10}\!\left(\frac{d}{r}\right). PR(r)=PR(d)+10nlog10(rd).
于是点概率为
Pr{PR(r)>γ}=Pr{Xσ>γ−PR(r)‾}=12erfc (γ−PR(r)‾σ2). \Pr\{P_R(r)>\gamma\} =\Pr\left\{X_\sigma>\gamma-\overline{P_R(r)}\right\} =\frac12\operatorname{erfc}\!\left( \frac{\gamma-\overline{P_R(r)}}{\sigma\sqrt2} \right). Pr{PR(r)>γ}=Pr{Xσ>γ−PR(r)}=21erfc(σ2 γ−PR(r)).
定义
a=γ−PR(d)‾σ2,b=10nlog10(e)σ2, a=\frac{\gamma-\overline{P_R(d)}}{\sigma\sqrt2}, \qquad b=\frac{10n\log_{10}(e)}{\sigma\sqrt2}, a=σ2 γ−PR(d),b=σ2 10nlog10(e),
并注意 log10(d/r)=log10(e)ln(d/r)\log_{10}(d/r)=\log_{10}(e)\ln(d/r)log10(d/r)=log10(e)ln(d/r),则
γ−PR(r)‾σ2=γ−PR(d)‾−10nlog10(d/r)σ2=a−bln (dr). \frac{\gamma-\overline{P_R(r)}}{\sigma\sqrt2} =\frac{\gamma-\overline{P_R(d)}-10n\log_{10}(d/r)}{\sigma\sqrt2} =a-b\ln\!\left(\frac{d}{r}\right). σ2 γ−PR(r)=σ2 γ−PR(d)−10nlog10(d/r)=a−bln(rd).
故
Pr{PR(r)>γ}=12erfc (a−bln dr). \Pr\{P_R(r)>\gamma\} =\frac12\operatorname{erfc}\!\left(a-b\ln\!\frac{d}{r}\right). Pr{PR(r)>γ}=21erfc(a−blnrd).
D.2 面积平均:极坐标积分
面积比例是把点概率按面积权重平均:
F(γ)=1πd2∫02π∫0dPr{PR(r)>γ} r dr dθ=∫0d2rd2Pr{PR(r)>γ} dr. F(\gamma)=\frac{1}{\pi d^2}\int_0^{2\pi}\int_0^d \Pr\{P_R(r)>\gamma\}\,r\,dr\,d\theta =\int_0^d \frac{2r}{d^2}\Pr\{P_R(r)>\gamma\}\,dr. F(γ)=πd21∫02π∫0dPr{PR(r)>γ}rdrdθ=∫0dd22rPr{PR(r)>γ}dr.
代入点概率:
F(γ)=∫0drd2erfc (a−bln dr)dr. F(\gamma)=\int_0^d \frac{r}{d^2}\operatorname{erfc}\!\left(a-b\ln\!\frac{d}{r}\right)dr. F(γ)=∫0dd2rerfc(a−blnrd)dr.
令变量代换
x=ln (dr)⇒r=de−x, dr=−de−xdx. x=\ln\!\left(\frac{d}{r}\right) \quad\Rightarrow\quad r=de^{-x},\ dr=-de^{-x}dx. x=ln(rd)⇒r=de−x, dr=−de−xdx.
当 r=dr=dr=d 时 x=0x=0x=0;当 r→0+r\to 0^+r→0+ 时 x→∞x\to\inftyx→∞。并且
rd2dr=de−xd2⋅(−de−xdx)=−e−2xdx. \frac{r}{d^2}dr =\frac{de^{-x}}{d^2}\cdot(-de^{-x}dx) =-e^{-2x}dx. d2rdr=d2de−x⋅(−de−xdx)=−e−2xdx.
因此
F(γ)=∫0∞e−2xerfc(a−bx) dx. F(\gamma)=\int_{0}^{\infty} e^{-2x}\operatorname{erfc}(a-bx)\,dx. F(γ)=∫0∞e−2xerfc(a−bx)dx.
D.3 做分部积分得到闭式
令
u=erfc(a−bx),dv=e−2xdx, u=\operatorname{erfc}(a-bx),\qquad dv=e^{-2x}dx, u=erfc(a−bx),dv=e−2xdx,
则
du=2bπe−(a−bx)2dx,v=−12e−2x. du=\frac{2b}{\sqrt{\pi}}e^{-(a-bx)^2}dx, \qquad v=-\frac12 e^{-2x}. du=π 2be−(a−bx)2dx,v=−21e−2x.
分部积分:
∫0∞e−2xerfc(a−bx) dx=[−12e−2xerfc(a−bx)]0∞+12∫0∞e−2x⋅2bπe−(a−bx)2dx. \int_0^\infty e^{-2x}\operatorname{erfc}(a-bx)\,dx =\left[-\frac12 e^{-2x}\operatorname{erfc}(a-bx)\right]_0^\infty +\frac12\int_0^\infty e^{-2x}\cdot \frac{2b}{\sqrt{\pi}}e^{-(a-bx)^2}dx. ∫0∞e−2xerfc(a−bx)dx=[−21e−2xerfc(a−bx)]0∞+21∫0∞e−2x⋅π 2be−(a−bx)2dx.
边界项:当 x→∞x\to\inftyx→∞,e−2x→0e^{-2x}\to 0e−2x→0,边界为 0;当 x=0x=0x=0,边界为 −12erfc(a)-\frac12\operatorname{erfc}(a)−21erfc(a),因此边界贡献是 +12erfc(a)+\frac12\operatorname{erfc}(a)+21erfc(a)。
于是
F(γ)=12erfc(a)+bπ∫0∞exp [−2x−(a−bx)2]dx. F(\gamma)=\frac12\operatorname{erfc}(a) +\frac{b}{\sqrt{\pi}}\int_0^\infty \exp\!\left[-2x-(a-bx)^2\right]dx. F(γ)=21erfc(a)+π b∫0∞exp[−2x−(a−bx)2]dx.
把指数配方:
−2x−(a−bx)2=−2x−(a2−2abx+b2x2)=−(b2x2−2x(ab−1)+a2). -2x-(a-bx)^2 =-2x-(a^2-2abx+b^2x^2) =-(b^2x^2-2x(ab-1)+a^2). −2x−(a−bx)2=−2x−(a2−2abx+b2x2)=−(b2x2−2x(ab−1)+a2).
令
b2x2−2x(ab−1)=b2[x2−2xab−1b2]=b2[(x−ab−1b2)2−(ab−1b2)2]. b^2x^2-2x(ab-1) =b^2\left[x^2-2x\frac{ab-1}{b^2}\right] =b^2\left[\left(x-\frac{ab-1}{b^2}\right)^2-\left(\frac{ab-1}{b^2}\right)^2\right]. b2x2−2x(ab−1)=b2[x2−2xb2ab−1]=b2[(x−b2ab−1)2−(b2ab−1)2].
所以
−2x−(a−bx)2=−b2(x−ab−1b2)2+(ab−1)2b2−a2. -2x-(a-bx)^2 =-b^2\left(x-\frac{ab-1}{b^2}\right)^2 +\frac{(ab-1)^2}{b^2}-a^2. −2x−(a−bx)2=−b2(x−b2ab−1)2+b2(ab−1)2−a2.
因此
∫0∞e−2x−(a−bx)2dx=exp ((ab−1)2b2−a2)∫0∞exp [−b2(x−ab−1b2)2]dx. \int_0^\infty e^{-2x-(a-bx)^2}dx =\exp\!\left(\frac{(ab-1)^2}{b^2}-a^2\right) \int_0^\infty \exp\!\left[-b^2\left(x-\frac{ab-1}{b^2}\right)^2\right]dx. ∫0∞e−2x−(a−bx)2dx=exp(b2(ab−1)2−a2)∫0∞exp[−b2(x−b2ab−1)2]dx.
再令
y=b(x−ab−1b2)⇒dx=dyb. y=b\left(x-\frac{ab-1}{b^2}\right)\Rightarrow dx=\frac{dy}{b}. y=b(x−b2ab−1)⇒dx=bdy.
当 x=0x=0x=0 时 y=b(0−ab−1b2)=1−abby=b\left(0-\frac{ab-1}{b^2}\right)=\frac{1-ab}{b}y=b(0−b2ab−1)=b1−ab;当 x→∞x\to\inftyx→∞ 时 y→∞y\to\inftyy→∞。于是
∫0∞exp [−b2(x−ab−1b2)2]dx=1b∫(1−ab)/b∞e−y2dy=π2berfc (1−abb). \int_0^\infty \exp\!\left[-b^2\left(x-\frac{ab-1}{b^2}\right)^2\right]dx =\frac{1}{b}\int_{(1-ab)/b}^{\infty}e^{-y^2}dy =\frac{\sqrt{\pi}}{2b}\operatorname{erfc}\!\left(\frac{1-ab}{b}\right). ∫0∞exp[−b2(x−b2ab−1)2]dx=b1∫(1−ab)/b∞e−y2dy=2bπ erfc(b1−ab).
综合起来:
F(γ)=12erfc(a)+bπ⋅exp ((ab−1)2b2−a2)⋅π2berfc (1−abb). F(\gamma)=\frac12\operatorname{erfc}(a) +\frac{b}{\sqrt{\pi}}\cdot \exp\!\left(\frac{(ab-1)^2}{b^2}-a^2\right)\cdot \frac{\sqrt{\pi}}{2b}\operatorname{erfc}\!\left(\frac{1-ab}{b}\right). F(γ)=21erfc(a)+π b⋅exp(b2(ab−1)2−a2)⋅2bπ erfc(b1−ab).
指数项化简:
(ab−1)2b2−a2=a2b2−2ab+1b2−a2=1−2abb2. \frac{(ab-1)^2}{b^2}-a^2 =\frac{a^2b^2-2ab+1}{b^2}-a^2 =\frac{1-2ab}{b^2}. b2(ab−1)2−a2=b2a2b2−2ab+1−a2=b21−2ab.
最终得到
F(γ)=12[erfc(a)+exp(1−2abb2)erfc (1−abb)], F(\gamma)=\frac12\left[ \operatorname{erfc}(a)+ \exp\left(\frac{1-2ab}{b^2}\right)\operatorname{erfc}\!\left(\frac{1-ab}{b}\right) \right], F(γ)=21[erfc(a)+exp(b21−2ab)erfc(b1−ab)],
这就是原文式 (14)。
附录 E:SV 模型中"泊松到达 ⇒ 指数间隔"的证明要点(对应式 (16)(19))
泊松过程的定义之一是:在任意长度为 Δt\Delta tΔt 的小时间区间内,发生一次事件的概率近似为 ΛΔt\Lambda \Delta tΛΔt,发生两次及以上是高阶小量;且不相交区间独立。由此可以证明"等待时间" WWW(从当前时刻到下一次事件的间隔)服从指数分布:
Pr{W>w}=e−Λw⇒fW(w)=Λe−Λw, w≥0. \Pr\{W>w\}=e^{-\Lambda w}\quad\Rightarrow\quad f_W(w)=\Lambda e^{-\Lambda w},\ w\ge 0. Pr{W>w}=e−Λw⇒fW(w)=Λe−Λw, w≥0.
于是簇到达时间满足 Tl−Tl−1∼Exp(Λ)T_l-T_{l-1}\sim \text{Exp}(\Lambda)Tl−Tl−1∼Exp(Λ),写成条件密度就是原文式 (16);同理,簇内射线间隔 τkl−τ(k−1)l∼Exp(λ)\tau_{kl}-\tau_{(k-1)l}\sim \text{Exp}(\lambda)τkl−τ(k−1)l∼Exp(λ),写成条件密度就是原文式 (19)。
附录 F:瑞利幅度式 (20) 与高斯生成式 (23) 的推导("复高斯幅度的模")
令
X∼N(0,σ2),Y∼N(0,σ2),X⊥Y. X\sim\mathcal{N}(0,\sigma^2),\quad Y\sim\mathcal{N}(0,\sigma^2), \quad X\perp Y. X∼N(0,σ2),Y∼N(0,σ2),X⊥Y.
定义复随机变量 Z=X+jYZ=X+jYZ=X+jY。其幅度
R=∣Z∣=X2+Y2. R=|Z|=\sqrt{X^2+Y^2}. R=∣Z∣=X2+Y2 .
在极坐标中,二维高斯的联合密度为
fX,Y(x,y)=12πσ2exp (−x2+y22σ2). f_{X,Y}(x,y)=\frac{1}{2\pi\sigma^2}\exp\!\left(-\frac{x^2+y^2}{2\sigma^2}\right). fX,Y(x,y)=2πσ21exp(−2σ2x2+y2).
变量变换到 x=rcosθ,y=rsinθx=r\cos\theta, y=r\sin\thetax=rcosθ,y=rsinθ 的雅可比为 rrr,故
fR,Θ(r,θ)=12πσ2exp (−r22σ2)⋅r. f_{R,\Theta}(r,\theta) =\frac{1}{2\pi\sigma^2}\exp\!\left(-\frac{r^2}{2\sigma^2}\right)\cdot r. fR,Θ(r,θ)=2πσ21exp(−2σ2r2)⋅r.
对 θ\thetaθ 积分得到幅度密度
fR(r)=∫02πfR,Θ(r,θ)dθ=rσ2exp (−r22σ2),r≥0, f_R(r)=\int_0^{2\pi}f_{R,\Theta}(r,\theta)d\theta =\frac{r}{\sigma^2}\exp\!\left(-\frac{r^2}{2\sigma^2}\right),\quad r\ge 0, fR(r)=∫02πfR,Θ(r,θ)dθ=σ2rexp(−2σ2r2),r≥0,
这就是瑞利分布。其二阶矩满足 E[R2]=2σ2E[R^2]=2\sigma^2E[R2]=2σ2,因此若希望 E[αkl2]E[\alpha_{kl}^2]E[αkl2] 等于某个给定值,只需取 σ=E[αkl2]/2\sigma=\sqrt{E[\alpha_{kl}^2]/2}σ=E[αkl2]/2 ,这正是原文式 (23) 所用的标定方式;而原文式 (20) 只是把瑞利密度用 E[αkl2]E[\alpha_{kl}^2]E[αkl2] 表示出来的同一件事。
附录 G:时间反转为什么产生"相关峰"(对图 8 的数学解释)
把室内信道在离散多径形式下写为
h(τ)=∑iαiejθiδ(τ−τi). h(\tau)=\sum_{i}\alpha_i e^{j\theta_i}\delta(\tau-\tau_i). h(τ)=i∑αiejθiδ(τ−τi).
时间反转预滤波器为
hTR(τ)=h∗(−τ)=∑iαie−jθiδ(τ+τi). h_{\text{TR}}(\tau)=h^*(-\tau)=\sum_i \alpha_i e^{-j\theta_i}\delta(\tau+\tau_i). hTR(τ)=h∗(−τ)=i∑αie−jθiδ(τ+τi).
复合响应
hcomp(τ)=hTR∗h=∫h∗(−λ) h(τ−λ) dλ. h_{\text{comp}}(\tau)=h_{\text{TR}}*h =\int h^*(-\lambda)\,h(\tau-\lambda)\,d\lambda. hcomp(τ)=hTR∗h=∫h∗(−λ)h(τ−λ)dλ.
把离散形式代入:
hcomp(τ)=∑i∑mαiαmej(θm−θi)δ(τ−(τm−τi)). h_{\text{comp}}(\tau) =\sum_{i}\sum_{m}\alpha_i\alpha_m e^{j(\theta_m-\theta_i)} \delta(\tau-(\tau_m-\tau_i)). hcomp(τ)=i∑m∑αiαmej(θm−θi)δ(τ−(τm−τi)).
当 τ=0\tau=0τ=0 时,满足 τm−τi=0⇒m=i\tau_m-\tau_i=0\Rightarrow m=iτm−τi=0⇒m=i,于是"对角项"贡献为
hcomp(0)=∑iαi2, h_{\text{comp}}(0)=\sum_i \alpha_i^2, hcomp(0)=i∑αi2,
所有项都是正的、同相累加,因此峰值很大。
当 τ≠0\tau\neq 0τ=0 时,主要由 m≠im\neq im=i 的交叉项构成:
∑i≠mαiαmej(θm−θi)δ(τ−(τm−τi)). \sum_{i\neq m}\alpha_i\alpha_m e^{j(\theta_m-\theta_i)}\delta(\tau-(\tau_m-\tau_i)). i=m∑αiαmej(θm−θi)δ(τ−(τm−τi)).
若环境丰富散射导致相位差 θm−θi\theta_m-\theta_iθm−θi 近似均匀分布、不同路径近似不相关,那么这些交叉项在统计平均意义上会相互抵消(期望接近 0),因此非零延迟处的幅度相对小。于是自相关函数出现一个突出的"零延迟峰",这正是图 8(b) 的尖峰来源,也是论文所说"能量集中"的数学本质。