对于某个单元来说,假设来自其他处理单元i的信息x,他们与本单元相互作用强度的连接权值为w,那么本处理单元的输入为
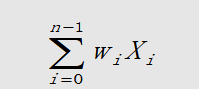
而处理单元的输出为:
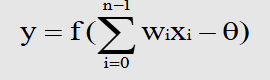
式中,x为第i个元素的输入,w为第i个处理单元与本处理单元的互联权值。f称为激发函数,决定了节点的输出。一般激发函数是非线性的,常用的非线性激发函数为:
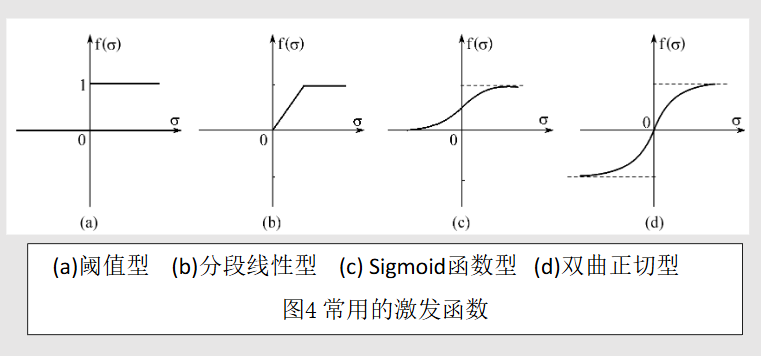
a为阶跃函数,表示激活值和其输出之间的关系,这是最简单的人工神经元,也就是M-P模型。
b线性分段函数是最简单的非线性函数,其将函数的值域限制在一定范围之内。
c是一个有最大输出值的非线性函数,输出值是在某个范围内的连续取值,以他为激发函数的神经元也有饱和特性。
d是特殊的c
二、人工神经网络的结构
常见的模型有:前向网络、从输入层到输出层、层内互联网络、互联网络。按性能分:连续型和离散型网络,或确定形和随机形网络。按拓扑结构分:有反馈网络和无反馈网络;按学习方法分:有教师和无教师;按突触来分:一阶线性关联网络和高阶非线性关联网络。
人工神经网络主要是为了模拟人的思维,同时能够并行处理,具有较强的学习能力,容错能力和联想能力。
三、感知机模型
首先把连接权和阈值初始化为较小的非零随机数,然后把有n个连接权值的输入送入网络,经加权运算处理,得到的输出如果与所期望的输出有较大的差别,就对连接权值参数按照某种算法进行自动调整,经过多次反复,直到所得到的输出与所期望的输出间的差别满足要求为止。
单层感知器不能表达的问题就是线性不可分问题,比如异或,由于单层感知机输出为
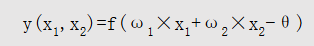
可以轻松实现与 或 非计算,但是异或只有两个输入和一个输出,分析起来简单,对于复杂的多输入函数来说多少是线性可分?多少是不可分?相关研究说明,线性不可分函数的数量随着输入变量个数的增加而快速增加,远远超出线性可分的个数,也就是说单层感知机不能表达的问题数量远超能表达问题。
3.1 多层感知机(MLP)
在单层感知器的输入部分和输出层之间加入一层或多层处理单元,就构成了二层或多层感知器。
在多层感知器模型中,只允许某一层的连接权值可调,这是因为无法知道网络隐层的神经元的理想输出,因而难以给出一个有效的多层感知器学习算法。多层感知器克服了单层感知器的许多缺点,原来一些单层感知器无法解决的问题,在多层感知器中就可以解决。例如,应用二层感知器就可以解决异或逻辑运算问题。
3.2 采用反向传播算法的多层感知机
MLP可以实现任意复杂的非线性映射关系用于分类
三层网络(一个隐层)可以实现空间内任意凸形成区域的划分。
四层网可以实现任意形状区域划分
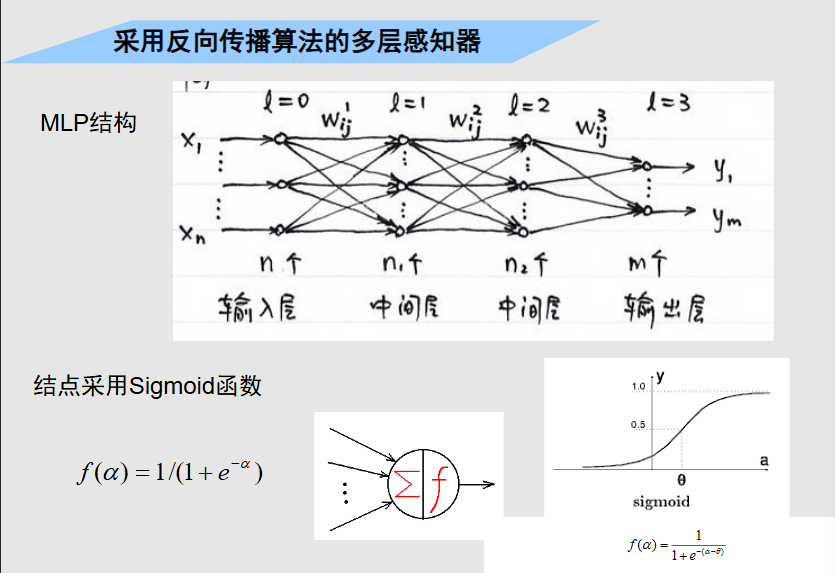
反向传播模型也称作b-p模型,是一种用于前向多层的反向传播学习算法,他可以对组成前向多层网络的各人工神经元之间的连接权值进行不断的修改,从而使前向多层网络能够将输入他的信号变成所期望的输出信息,因此被称作学习方法。反向学习算法是因为在修改各个神经元的连接权值时,所依据的是该网络的实际输出和期望输出之差,将这一差值方向一层层的向回传播,来决定连接权值的修改。因此bp的网络结果是一个前向多层网络。
bp算法的学习目的是对网络的连接权值进行调整,使调整后的网络对任一输入都能得到期望的输出。正向传播用于对前向网络进行计算,即对某一输入信息,经过网络计算后求出它的输出结果。反向传播用于逐层传递误差,修改神经元间连接的权值,以使网络对输入信息经过计算后所得到的输出能达到期望误差要求。

在以上过程中,5尤其重要,如何确定一种调节连接权值的原则,使误差沿着最小的方向发展,是BP必须解决的问题


六、用多层感知机网络实现模式识别

