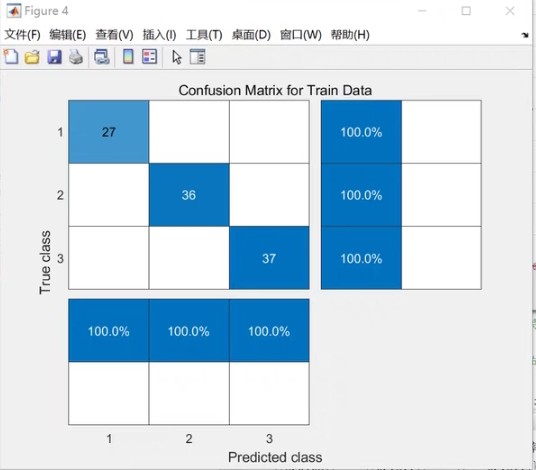
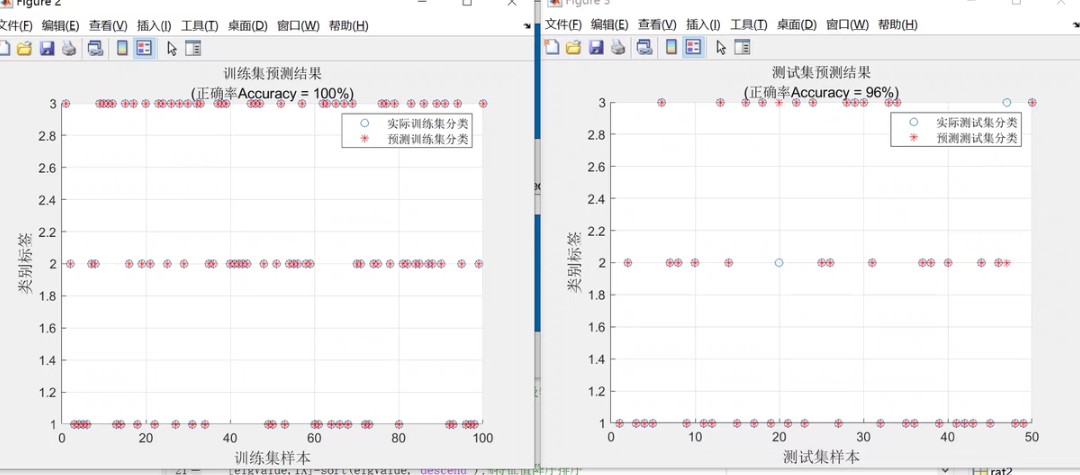
PCA-RF主成分分析降维后用随机森林模型进行分类 matlab代码 利用主成分对高维数据进行降维, 将输入RF模型内的自变量数据量降低, 进实现提高模型精度的目的, 然后PCA-RF是随机森林模型组合,做分类建模。 注: 1.程序内有详细注释, 2.无需更改代码,替换数据集即可运行...
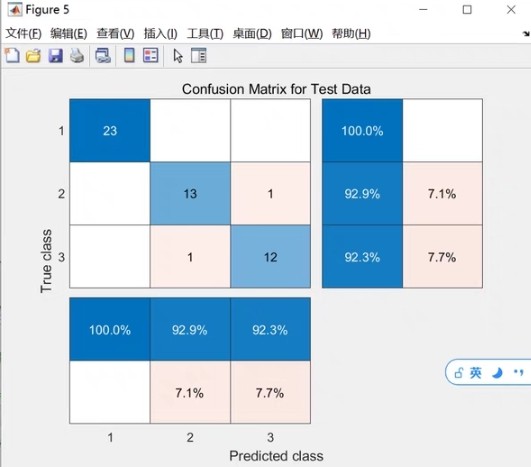
在数据处理和机器学习领域,面对高维数据时,我们常常会遇到诸如维度灾难等问题,这不仅增加了计算成本,还可能影响模型的精度。今天咱们就来聊聊如何利用PCA(主成分分析)对数据降维,再结合RF(随机森林)模型进行分类,以实现更好的效果。
PCA原理与作用
PCA旨在通过线性变换,将原始高维数据转换到一组新的正交基上,这些新基按照数据方差大小排序。保留方差较大的几个主成分,就能在损失较少信息的情况下降低数据维度。比如,假设我们有一个包含大量特征的数据集,其中某些特征之间可能存在高度相关性,PCA可以找到那些最能代表数据变异性的特征组合,从而简化数据。
RF模型简介
随机森林是一种基于决策树的集成学习算法。它通过从原始数据集中有放回地采样,构建多棵决策树,然后综合这些决策树的预测结果(如分类时采用多数投票法)来做出最终决策。随机森林在处理复杂数据集、防止过拟合方面表现出色。
PCA - RF结合的优势
将PCA与RF结合,利用PCA对高维数据降维,减少输入RF模型的自变量数据量。一方面降低了计算复杂度,另一方面去除了一些冗余信息,理论上可以提高模型精度。这就好比给随机森林这个"大厨"准备食材,PCA先把一堆复杂且有些重复的食材精简处理,让大厨能更高效地做出美味(准确的预测)。
Matlab代码实现
matlab
% 假设我们有一个高维数据集data,每一行代表一个样本,每一列代表一个特征
load('your_data_file.mat'); % 加载数据集,需替换为实际数据集文件名
data = your_data; % 替换为实际数据变量名
% PCA降维
[coeff,score,latent] = pca(data);
% coeff是主成分系数矩阵,每一列是一个主成分的系数
% score是降维后的数据矩阵,每一行是一个样本在新坐标系下的坐标
% latent是每个主成分对应的方差
num_components = 5; % 根据需要选择保留的主成分数量,这里以5为例
reduced_data = score(:,1:num_components);
% 随机森林分类模型
X = reduced_data; % 降维后的数据作为自变量
Y = your_labels; % 样本对应的标签,需替换为实际标签变量名
% 创建并训练随机森林模型
tree = TreeBagger(50,X,Y,'Method','classification');
% 50表示构建50棵决策树,可根据情况调整
% 预测
new_data = [1 2 3 4 5]; % 假设有新数据需要预测,需替换为实际新数据
predicted_label = predict(tree,new_data);
disp(['预测标签为:', num2str(predicted_label)]);代码分析
- PCA部分 :
pca函数是Matlab中用于主成分分析的核心函数。通过它,我们得到了主成分系数矩阵coeff、降维后的数据矩阵score以及每个主成分对应的方差latent。之后根据需求选取一定数量的主成分,这里我们选了5个,构建出降维后的数据reduced_data。 - 随机森林部分 :使用
TreeBagger函数创建并训练随机森林模型。这里设置构建50棵决策树,将降维后的数据X和对应的标签Y作为输入。最后,对于新数据newdata*,使用训练好的模型tree进行预测,得到预测标签predicted*label。
通过上述的PCA - RF组合,我们就可以在高维数据的分类问题上迈出坚实的一步。当然,实际应用中还需要根据数据集的特点调整参数,比如PCA中保留的主成分数量、随机森林中决策树的数量等,以达到最佳的模型性能。希望这篇博文能给大家在处理类似问题时带来一些启发。