背包问题
背包问题是经典的动态规划 问题之一
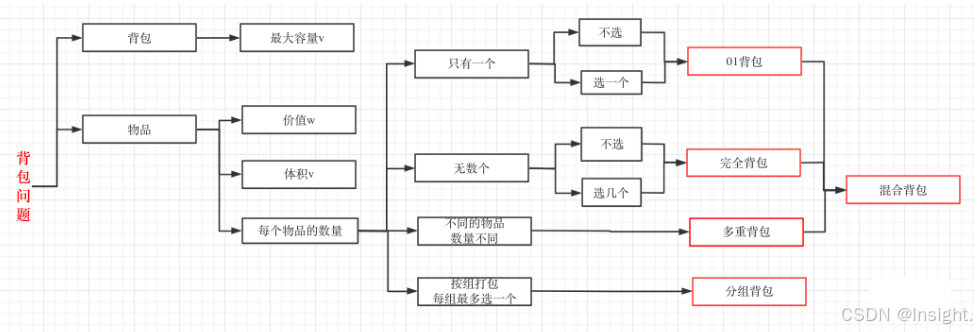
这里只讨论01背包、完全背包问题,其余的暂不讨论
动态规划五部曲:
- 确定dp数组(dp table)以及下标的含义
- 确定递推公式
- dp数组如何初始化
- 确定遍历顺序
- 举例推导dp数组
01背包
01背包指的是给定n个物品,每个物品有两个属性:
w[i]:第i个物品的重量(weight)v[i]:第i个物品的价值(value)
再给一个背包容量W(能承受的最大总重量),问我们:
从这
n个物品中选择若干个(每个物品最多只能选择一次 ),使得在不超过总容量W的前提下,获得的最大价值是多少?
力扣原题:
416. 分割等和子集
1049. 最后一块石头的重量 II
494. 目标和
474. 一和零
1.确定dp数组(dp table)以及下标的含义
我们初始化了如下的dp数组,其中行代表背包的可用容量,列代表可用的物品。dp[i][j]代表容量为j的背包装入前i个物品的最大价值
| 物品\容量 | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| 0 | |||||
| 1 | |||||
| 2 | |||||
| 3 | |||||
| 4 |
2.dp数组初始化
对于容量为0的背包,面对所有的物品选择都只能不装入,因此所有的价值都是0,对于任意容量的背包,不选择物品的价值都是0
| 物品\容量 | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | ||||
| 2 | 0 | ||||
| 3 | 0 | ||||
| 4 | 0 |
3.确定递推公式
在我们选择第i个物品时有两种选择方案:
1.不将当前物品装入背包
2.将当前物品装入背包
将当前第i物品装入背包时,我们的价值为:
1.不将物品装入背包,因此价值为相同容量下选择i-1个物品的价值,即dp[i][j] = dp[i-1][j]
2.将物品装入背包,因此价值为容量j-w[i]下的价值加上当前物品的价值,即dp[i][j] = dp[i-1][j - w[i]] + v[i]
综合来说,dp[i][j] = max(dp[i-1][j], dp[i-1][j - w[i]] + v[i])
4.确定遍历顺序
先按行遍历,再按列遍历,从1开始
完全背包
完全背包指的是给定n个物品,每个物品有两个属性:
w[i]:第i个物品的重量(weight)v[i]:第i个物品的价值(value)
再给一个背包容量W(能承受的最大总重量),问我们:
从这
n个物品中选择若干个(每个物品可以选择多次 ),使得在不超过总容量W的前提下,获得的最大价值是多少?
力扣原题:
518. 零钱兑换 II
377. 组合总和 Ⅳ
322. 零钱兑换
279. 完全平方数
139. 单词拆分