2D摄影几何变换 - 1
2D摄影几何变换 - 1
- [2D摄影几何变换 - 1](#2D摄影几何变换 - 1)
- 一、平面几何
- 二、2D摄影平面
-
- 1、点与直线
- [2、 理想点与无穷远线](#2、 理想点与无穷远线)
- [3、 二次曲线和对偶二次曲线](#3、 二次曲线和对偶二次曲线)
- 三、射影变换
前言:《计算机视觉中的多视图几何》这本书我其实反复读过好几遍,但常常中途放下,或是只挑当前急需的章节来看,总觉得知识体系还没能完整建立起来。这次下定决心要把它从头到尾认真学完------虽然理论部分难免枯燥,但扎实的基础离不开系统的积累。加油吧,一步步来!
一、平面几何
在计算机视觉中的多视图几何一书中,将使用混合的方法(几何和代数的方法)。在代数方法中,几何实体用坐标和代数实体描述 。在几何中采用代数方法的显著优点是:这种方法导出的结果更容易产生算法以及实际的计算方法。
二、2D摄影平面
平面上的一点可以用 I R 2 IR^2 IR2 中的一对坐标 ( x , y ) (x,y) (x,y)来表示,因此,通常 I R 2 IR^2 IR2 等同于一张平面。把 I R 2 IR^2 IR2 看做一个矢量空间时,坐标对 ( x , y ) (x,y) (x,y) 是矢量,也就是说点等同于矢量。
齐次表示: 齐次表示是数学和计算机科学(特别是计算机图形学、机器人和几何计算)中常用的一种技巧,它通过增加一个维度(通常是1或0)来将点、向量、平移、旋转等几何元素用统一的矩阵形式来表示和计算。
行和列矢量 几何实体用列矢量表示,它的转置是行矢量。
1、点与直线
直线的齐次表示: 平面上的一条直线可用形如 a x + b y + c = 0 ax+by+c=0 ax+by+c=0 的方程表示, a , b , c a,b,c a,b,c 的不同值给出不同的直线。因此,一条直线也可以用矢量 ( a , b , c ) T (a,b,c)^T (a,b,c)T 表示。直线和矢量 ( a , b , c ) T (a,b,c)^T (a,b,c)T 不是一一对应的,因为,对任何非零 k k k, 直线 a x + b y + c = 0 ax+by+c=0 ax+by+c=0 与直线 ( k a ) x + ( k b ) y + ( k c ) = 0 (ka)x+(kb)y+(kc)=0 (ka)x+(kb)y+(kc)=0 相同。因此,对任何非零 k k k, 矢量 ( a , b , c ) T (a,b,c)^T (a,b,c)T与 k ( a , b , c ) T k(a,b,c)^T k(a,b,c)T表示同一直线。事实上,我们视这两个只相差一个全局缩放因子的矢量是等价的。这种等价关系下的矢量等价类被称为齐次矢量。任何具体矢量 ( a , b , c ) T (a,b,c)^T (a,b,c)T 是所属的等价类的一个代表。在 I R 3 − ( 0 , 0 , 0 ) T IR^3-(0,0,0)^T IR3−(0,0,0)T 中的矢量等价类的几何组成射影空间 I P 2 IP^2 IP2。记号: − ( 0 , 0 , 0 ) T -(0,0,0)^T −(0,0,0)T 表示矢量 ( 0 , 0 , 0 ) T (0,0,0)^T (0,0,0)T 不与任何直线对应,因而被排除在外。
点的齐次表示: 点 x = ( x , y ) T x=(x,y)^T x=(x,y)T 在直线 l = ( a , b , c ) T l=(a,b,c)^T l=(a,b,c)T 上的充要条件是 a x + b y + c = 0 ax+by+c=0 ax+by+c=0。并可用矢量内积形式把它表示为 ( x , y , 1 ) ( a , b , c ) T = ( x , y , 1 ) l = 0 (x,y,1)(a,b,c)^T=(x,y,1)l=0 (x,y,1)(a,b,c)T=(x,y,1)l=0,即把 "1" 作为增加的最后一个坐标使 I R 2 IR^2 IR2 中的点 ( x , y ) T (x,y)^T (x,y)T 表示成3维矢量。注意对任何非零 k k k 和直线 l l l,方程 ( k a , k b , k c ) l = 0 (ka,kb,kc)l=0 (ka,kb,kc)l=0 的充要条件是 ( a , b , 1 ) l = 0 (a,b,1)l=0 (a,b,1)l=0。因而,我们自然把由 k k k不为零的不同值所构成的矢量集 ( k x , k b , k c ) T (kx,kb,kc)^T (kx,kb,kc)T 看做是 I R 2 IR^2 IR2 中点 ( x , y ) T (x,y)^T (x,y)T 的一种表示。因此,与直线一样,点也可用齐次矢量表示。一个点的任何齐次矢量的标识形式为 x = ( x 1 , x 2 , x 3 ) T x=(x_1,x_2,x_3)^T x=(x1,x2,x3)T,并表示 I R 2 IR^2 IR2 的点 x = ( x 1 / x 2 , x 2 / x 3 ) T x=(x_1/x_2,x_2/x_3)^T x=(x1/x2,x2/x3)T。于是,点作为齐次矢量同样也是 I P 2 IP^2 IP2 的元素。
- 结论2.1 点 x x x 在直线 l l l 上的充要条件是 x T l = 0 x^Tl=0 xTl=0
自由度(dof): 自由度显然,为了指定一个点必须提供两个值,即它的 x x x 和 y y y 坐标。同样,一条直线由两个参数指定(两个独立的比率 a : b , c : b {a:b,c:b} a:b,c:b ) 因 而有两个自由度。例如,在非齐次表示中,这两个参数可以取为直线的梯度和 y y y 轴上的截距。
直线的交点: 给定两直线 I = ( a , b , c ) T I=(a,b,c)^T I=(a,b,c)T 和 I ′ = ( a ′ , b ′ , c ′ ) T I'=(a',b',c')^T I′=(a′,b′,c′)T,我们希望求它们的交点。定义矢量 x = l × l ′ x=l \times l' x=l×l′,由三重纯量积等式 l ⋅ ( l × l ′ ) = l ′ ⋅ ( l × l ′ ) = 0 l \cdot(l \times l')=l' \cdot(l \times l')=0 l⋅(l×l′)=l′⋅(l×l′)=0。推 出 l T x = l ′ T x = 0 l^Tx=l'^Tx=0 lTx=l′Tx=0 . 因此,如果把 x x x 视为一个点,则 x x x 同时在两条直线 I I I 和 l ′ l ' l′ 上,因而是两线的交点.
- 结论2.2 两直线 l l l 和 l ′ l' l′ 的交点是点 x = l × l ′ x=l\times l' x=l×l′
点的连线: 过两点 x x x 和 x ′ x' x′ 的 直 线 的 表示式可完全类似地导出.定义直线 l = x × x ′ l = x \times x ' l=x×x′,并不难验证点 x x x 和 x ′ x' x′ 都在 l l l 上。
- 结论 2.3 过两点 x x x 和 x ′ x' x′的直线是 l = x × x ′ l = x \times x ' l=x×x′ .
2、 理想点与无穷远线
平行线的交点: 考察两直线 a x + b y + c = 0 ax+by+c=0 ax+by+c=0 和 a x + b y + c ′ = 0 ax+by+c'=0 ax+by+c′=0. 它们可分别用矢量 l = ( a , b , c ) T l=(a,b,c)^T l=(a,b,c)T 和 l ′ = ( a , b , c ′ ) T l'=(a,b,c')^T l′=(a,b,c′)T 表示,其中它们的前两个坐标是一样的。用结论1.2不难算出这两条直线的交点为 l × l ′ = ( c ′ − c ) ( b , − a , 0 ) T l \times l'=(c'-c)(b,-a,0)^T l×l′=(c′−c)(b,−a,0)T, 忽略标量因子 ( c − c ′ ) (c-c') (c−c′),得到点 ( b , − a , 0 ) T (b,-a,0)^T (b,−a,0)T。现在,如果我们试图求这一点的非齐次表示 ,就会得到 ( b × 0 , a × 0 ) T (b \times 0, a \times 0)^T (b×0,a×0)T,它只能解释为该交 点有无穷大坐标。 一般地,具有齐次坐标 ( x , y , 0 ) T (x,y,0)^T (x,y,0)T 的点不与 I R 2 IR^2 IR2 中任何有限点对应这一观察与通常平行线交于元穷远的概念相吻合 。
理想点与无穷远线: 当 x 3 ≠ 0 x_3 \neq 0 x3=0 时,齐次矢量 x = ( x 1 , x 2 , x 3 ) T x=(x_1,x_2,x_3)^T x=(x1,x2,x3)T 我们可以把最后坐标为 x = 0 x=0 x=0 的点加入 I R 2 IR^2 IR2 。 所扩展的空间是所有齐次 3 维矢量的集合,称为射影空间 I P 2 IP^2 IP2 。 最后坐标为 x 3 = 0 x_3=0 x3=0 的点被称为理想点,或无穷远点。所有理想点的集合可以写成 ( x 1 , x 2 , 0 ) T (x_1,x_2,0)^T (x1,x2,0)T,并由比率 x 1 : x 2 x_1:x_2 x1:x2 指定一个具体的点。 注意该集合在一条直线上,称无穷远线 ,用矢量 I ∞ = ( 0 , 0 , 1 ) T I_\infty = (0 , 0 , 1)^T I∞=(0,0,1)T 表示 。我们可以验证 ( 0 , 0 , 1 ) ( x 1 , x 2 , 0 ) T = 0 (0 , 0 , 1)(x_1,x_2,0)^T=0 (0,0,1)(x1,x2,0)T=0
在非齐次表示下, ( b , − a ) T (b, -a)^T (b,−a)T 是与该直线相切的矢量,与该直线的法线 ( a , b ) T (a,b)^T (a,b)T 相正交,因而它代表该直线的方向。当直线的方向改变时,理想点 ( b , − a , 0 ) T (b, -a, 0)^T (b,−a,0)T 沿 I ∞ I_\infty I∞ 而变化。基于这些理由,无穷远线可以看作是平面上所有直线方向的集合。
摄影平面的模型: 一种有益的方法是把 I P 2 IP^2 IP2 看作 I R 3 IR^3 IR3 中一种射线的集合。该集合的所有矢量 k ( x 1 , x 2 , x 3 ) T k(x_1, x_2, x_3)^T k(x1,x2,x3)T 当 k k k 变化时形成过原点的射线。这样的一条射线可以看作是 I P 2 IP^2 IP2 中的一个点。在此模型中, I P 2 IP^2 IP2 中的直线是过原点的平面。可以验证两相异的射线共处于一张平面上,而任何两张相异平面相交于一条射线。这类似于两个相异的点唯一确定一条直线,而两条相异的直线总相交于一点。
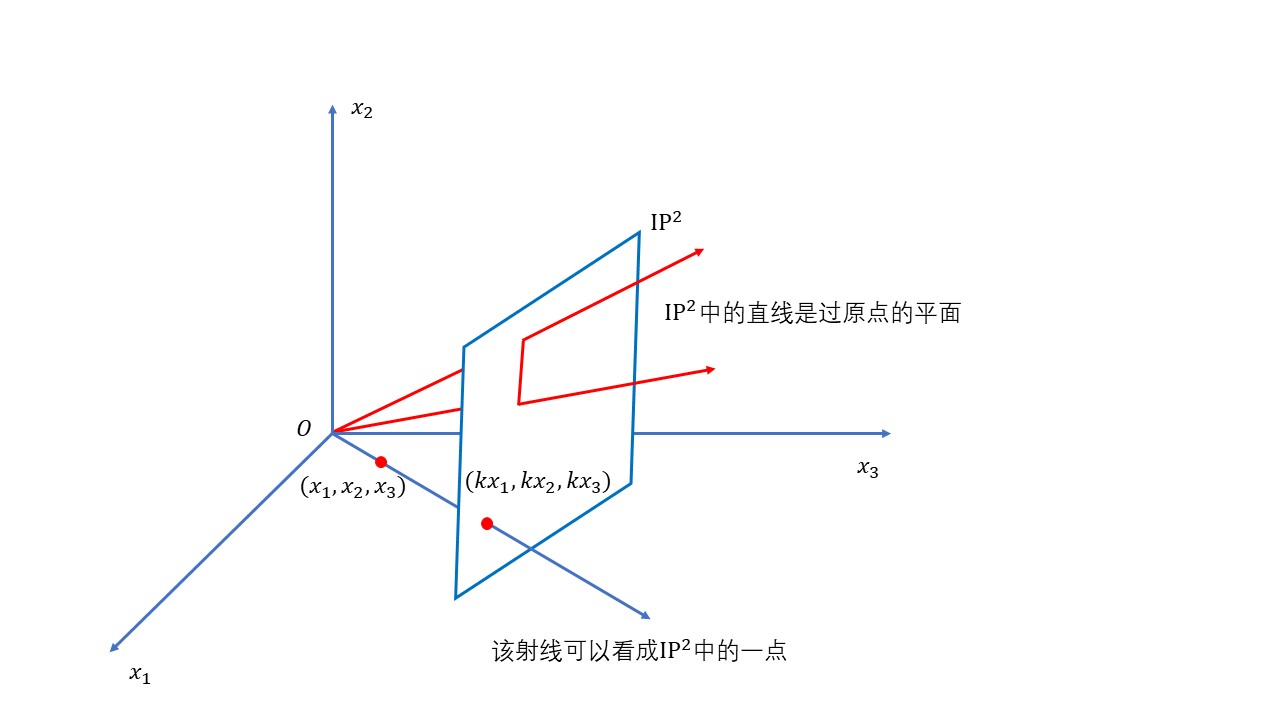
对偶: 在关于线和点的性质的陈述中,点和线的作用可以怎样互换。特别是,直线和点的基本接合方程式 l T x = 0 l^Tx=0 lTx=0 是对称的,因为 l T x = 0 l^Tx=0 lTx=0 意味着 x T l = 0 x^Tl=0 xTl=0 ,其中线和点的位置互相交换了。类似地,两线相交和一线过两点的结论1. 2 和 1. 3 ,当把点和线的作用互换后,其本质是一样的.由此得到一个如下的一般原理: 对偶原理:
- 结论2. 4 对偶原理 2 维射影几何中的任何定理都有一个对应的对偶定理,它可以通过互 换原定理中点和线的作用而导出 。
3、 二次曲线和对偶二次曲线
二次曲线由平面上的二阶方程描述。在欧氏几何中,二次曲线有三种主要类型:双曲线,椭圆和抛物线(后面将定义的所调的退化二次曲线除外), 在经典理论中, 这三类曲线是不同方向的平面与圆锥相交所产生的锁线(退化的二次曲线由过锥顶的平面产生)。但是我们将了解到,在 2D 射影几何中所有非退化的二次曲线在射影变换下都等价 。
在非齐欢坐标中,二次曲线的方程是:
a x 2 + b x y + c y 2 + d x + e y + f = 0 ax^2 + bxy + cy^2 + dx + ey + f = 0 ax2+bxy+cy2+dx+ey+f=0
对应于一个二阶多项式。过替代: x → x 1 / x 3 x→x_1 /x_3 x→x1/x3, y → x 2 / x 3 y→x_2/x_3 y→x2/x3,"齐次化"得到:
a x 1 2 + b x 1 x 2 + c x 2 2 + d x 1 x 3 + e x 2 x 3 + f x 3 2 = 0 ax_1^2 + bx_1x_2 + cx_2^2 + dx_1x_3 + ex_2x_3+ fx_3^2 = 0 ax12+bx1x2+cx22+dx1x3+ex2x3+fx32=0
或表示成矩阵形式:
X T C X = 0 X^TCX=0 XTCX=0
其中二次曲线系数矩阵C为:
C = [ a b / 2 d / 2 b / 2 c e / 2 d / 2 e / 2 f ] C=\begin{bmatrix} a & b/2 & d/2 \\ b/2 & c & e/2 \\ d/2 & e/2 & f\\ \end{bmatrix} C= ab/2d/2b/2ce/2d/2e/2f
二次曲线有五个自由度,可以视为比率 a : b : c : d : e : f a : b: c : d : e : f a:b:c:d:e:f 或等价地视为对称矩阵六个元素减去一个比例因子。
五点定义一条二次曲线
二次曲线的切线 在齐次坐标下,过二次曲线上点 x 的 切线 l 有特别简单的形式 :
结论2. 5 过(非退化)二次曲线 C 上点 x 的切线 1 由 I = Cx 确定。
对偶二次曲线 :上面定义的二次曲线 C 更确切地应称为点 二次曲线,因为它定义的是点的方程 。给出了 I P 2 IP^2 IP2 的对偶结论 1. 4 以后,理所监然应该有一个 由直线的方程定义的二次曲线。这种对偶 (或线) 二次曲线也由 一个 3x3 矩阵表示,我们把它记为 C ∗ C^* C∗ 二次曲线 C C C 的切线 l l l 满足 l T C l = 0 l^TCl=0 lTCl=0。 其中 C ∗ C^* C∗ 表示 C C C 的伴随矩阵。对非奇异对称矩阵 C C C 有 C ∗ = C − 1 C^* = C^{-1} C∗=C−1 (相差一个尺度因子) 。
对偶二次曲线也称二次曲线的包络,对偶二 次曲线有五个自由度 。与点二次曲线相类似,一般位置上的五条线定义一条对偶二次曲线。
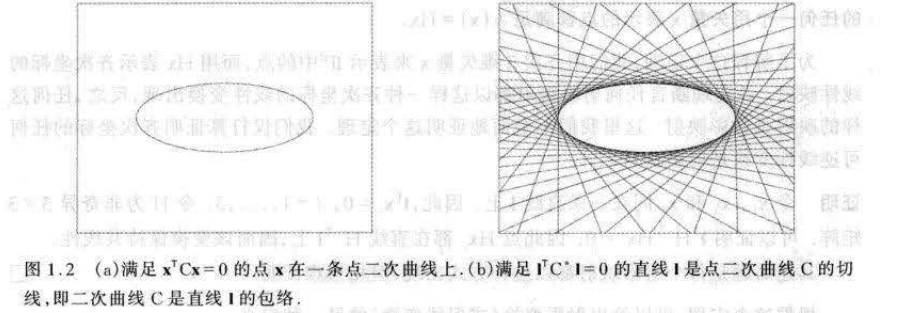
当 C 为满秩时,对偶二次曲线方程可直接推导,非满秩矩阵 C 所定义的二次曲线称作退化二次曲线。退化的点二次曲线包含两条线(秩 2)或一 条重线(秩 1)。
三、射影变换
几何研究的是在变换群下保持不变的性质。根据他的观点,2D 射影几何研究的是关于射影平面 I P 2 IP^2 IP2 在所谓射影映射的变换群下保持不变的性质。
**定义3.1 射影映射是 I P 2 IP^2 IP2 到它自身的一种满足下列条件的可逆映射 h h h:三点 x 1 , x 2 和 x 3 x_1, x_2和x_3 x1,x2和x3 共线当且仅当 h ( x 1 ) , h ( x 2 ) 和 h ( x 3 ) h(x_1), h(x_2) 和 h(x_3) h(x1),h(x2)和h(x3)也共线.
射影映射组成一个群,因为射影映射的逆以及两个射影映射的复合也是射影映射。射影映射也称为保线变换,或射影变换或单应 ( homography ) 。
**定理3.2 映射 h h h: I P 2 → I P 2 IP^2→IP^2 IP2→IP2 是射影映射的充要条件是 : 存在一个 3 X 3 3X3 3X3 非奇异矩阵 H H H , 使得 I P 2 IP^2 IP2 的任何一个用矢量 x x x 表示的点都满足 h ( X ) = H x h (X) = Hx h(X)=Hx。
**定义3.3 射影变换 平面射影变换是关于齐次3维矢量的一种线性变换,并可用一个非奇异 3 × 3 3 \times 3 3×3的矩阵 H H H 表示为:
x 1 ′ x 2 ′ x 3 ′ \] = \[ h 11 h 12 h 13 h 21 h 22 h 23 h 31 h 32 h 33 \] \[ x 1 x 2 x 3 \] \\begin{bmatrix} x_1' \\\\ x_2' \\\\ x_3' \\\\\\end{bmatrix} = \\begin{bmatrix} h_{11} \& h_{12} \& h_{13} \\\\ h_{21} \& h_{22} \& h_{23} \\\\ h_{31} \& h_{32} \& h_{33}\\end{bmatrix} \\begin{bmatrix} x_1 \\\\ x_2 \\\\ x_3\\end{bmatrix} x1′x2′x3′ = h11h21h31h12h22h32h13h23h33 x1x2x3 或更简洁地表示为 x ′ = H x x ' = Hx x′=Hx,在 H 的 丸个元 素中有人个独立比率,因此一个射影变换有八个自由度。 射影变换将每个图形投影为射影等价的图形,保持所有的射影性质不变 . 在图 1 . 1 的 射线模型中,一个射影变换就是 I R 3 IR\^3 IR3 的一种线性变换。 **平面之间的映射:** 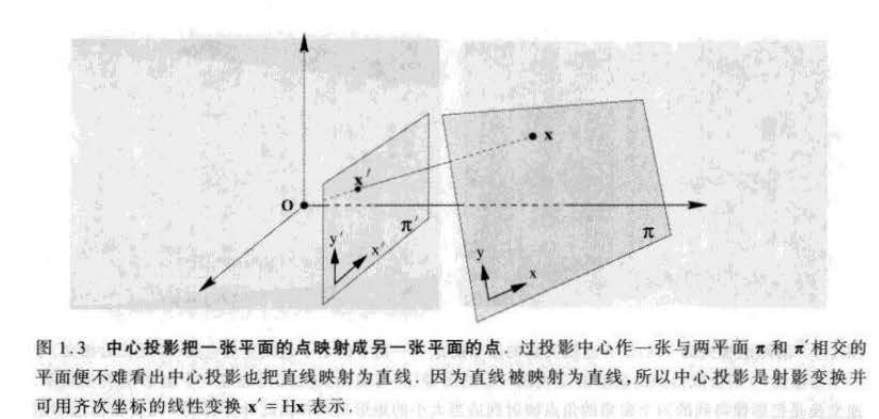 实际上,如果在两平面上建立的都是欧氏(直角)坐标系,那么这样一种由中心投影定义的映射比一般射影变换有更多的约束。我们称它为**透视映射**而不是完全的射影映射,它可由一个六自由度的变换来表示。 ### 1、直线与二次曲线的变换 **直线的变换:** 如果点 x x x,在直线 l l l 上,那么纯射影变换后的点在 x ′ = H x x'=Hx x′=Hx;在直线 l ′ = H − T l l'=H\^{-T}l l′=H−Tl 上。因为 l ′ T x ′ = l T H − 1 H x = 0 l'\^Tx'=l\^TH\^{-1}Hx=0 l′Tx′=lTH−1Hx=0,故变换 H H H 保持点在直线上的性质。它给出了关于直线的变换规则:在点变换 x ′ = H x x'=Hx x′=Hx 下,直线 l l l 变换为 l ′ = H − T l l ' = H\^{-T}l l′=H−Tl。 注意直线和点变换的基本区别。点变换依据 H H H,而直线 (视为行矢量)变换则依据 H − 1 H\^{-1} H−1。这可以用术语"协变"或"逆变"做解释。我们称点变换为逆变而线变换为协变。 ![!\[\[Pasted image 20251219152456.png\]\]](https://i-blog.csdnimg.cn/direct/c4de760f7f0b4aa59e5bc9613c4b9949.png) **二次曲线的变换** **结论3.4 在点变换 x ′ = H x x' = Hx x′=Hx 下 ,二次曲线 C C C 变换为 C ′ = H − T C H − 1 C' = H\^{-T}CH\^{-1} C′=H−TCH−1。** 因 H − L H\^{-L} H−L 出现在方程中,故可以称二次曲线变换为协变。对偶二次曲线的变换规则可用类似的方式导出,即: **结论3.5 在点变换 x ′ = H x x ' = Hx x′=Hx 下,对偶二次曲线 C ′ C' C′变换为 C ∗ ′ = H C ∗ H T C\^{\*'}=HC\^\*H\^T C∗′=HC∗HT。**