数据结构（四）图结构

烤盘饭大王2025-12-21 10:57

一、定义和基本概念

1.图（Graph）是一种 节点（顶点）与节点之间的关系（边） 的数据结构。

复制代码 
G = (V, E)     V：顶点集合（Vertices）    E：边的集合（Edges）

2.完全图： 任意两个不同顶点之间都存在一条边的图。（最稠密的图）

边数：有向完全图：n(n−1)，无向完全图：n(n−1)​/2

3.简单路径：路径中不出现相同顶点。

简单回路：**除了起点/终点，**路径中不出现相同顶点。

4.度：无向图-顶点的度指的是与顶点相关联边的数目；

有向图-讲究入度和出度。

  1. 无向图中，顶点度之和等于边数的两倍；

有向图中，所有顶点的出度之和与入度之和相等，弧的数量也相等。

6.连通图：对于图中任意两个顶点都是连通的。

（连通不是要求两个点有边，只要有路径就行）

7.连通分量：无向图中的极大连通子图（即再加一个点就不成立）。

8.在有向图中叫做：强连通图 ，强连通分量。

9.生成树：含有图中全部顶点的极小连通子树。

二、图的基本分类

1.有向图vs无向图

无向图：顶点 v 的度 = 与其连接的边数

有向图：入度,出度

2.有权图vs带权图（网，Network）

三、图的存储结构

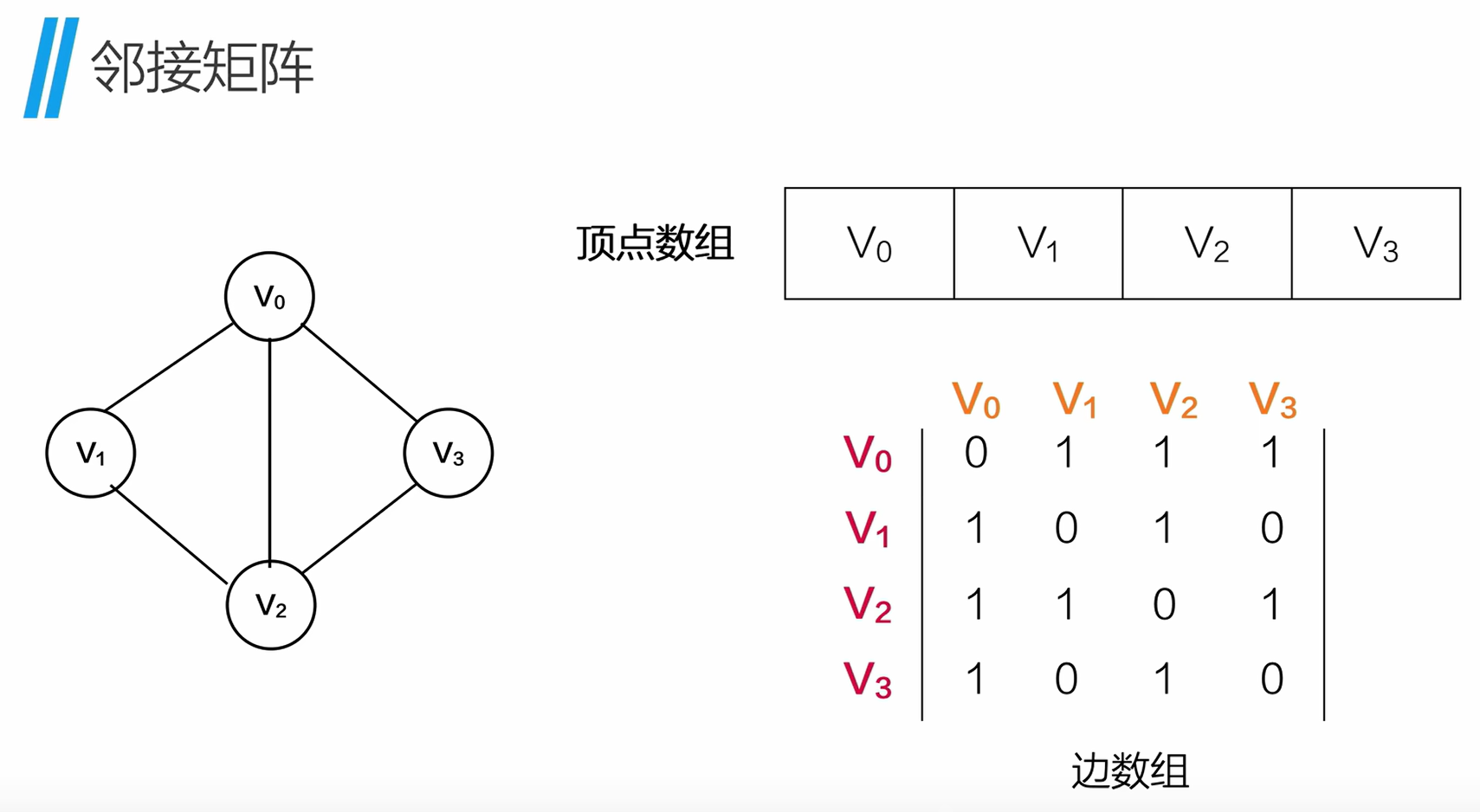
1.邻接矩阵

对 n 个顶点，用一个 n×n 的二维数组 表示边：

  • 无向图：对称矩阵 有向图：不对称

  • 无权图：0/1 有权图：权值/∞

优点

  • 查询是否有边：O(1)

  • 结构简单，适合稠密图

缺点

  • 占空间：O(n²)

  • 遍历顶点的邻接点效率不高

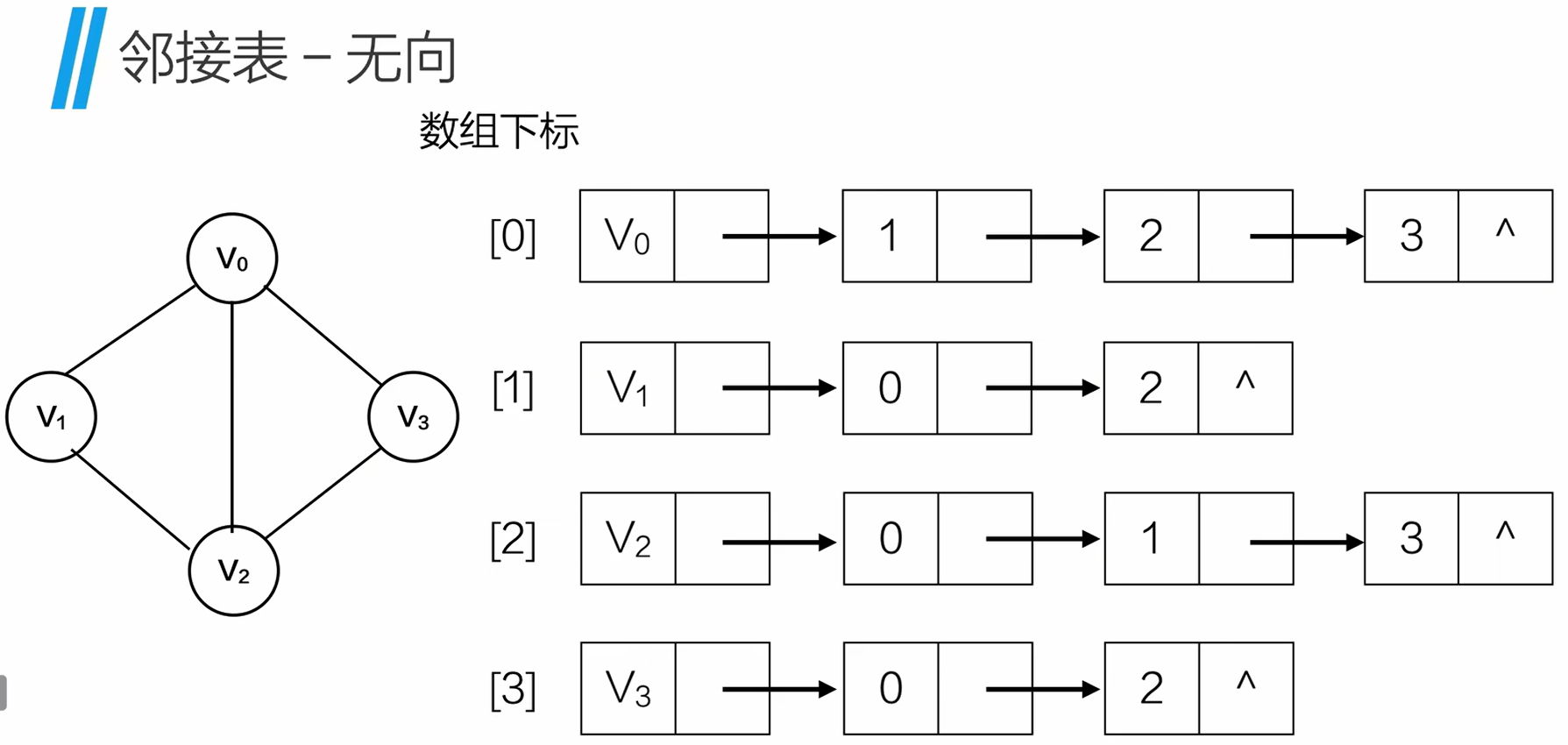
2.邻接表

每个顶点维护一个链表，存储与其相邻的顶点。

适用于稀疏图（边少）。

优点

  • 节省空间：O(n + m)

  • 方便遍历每个顶点的所有边

缺点

  • 查询某条边是否存在：需要 O(度(v))

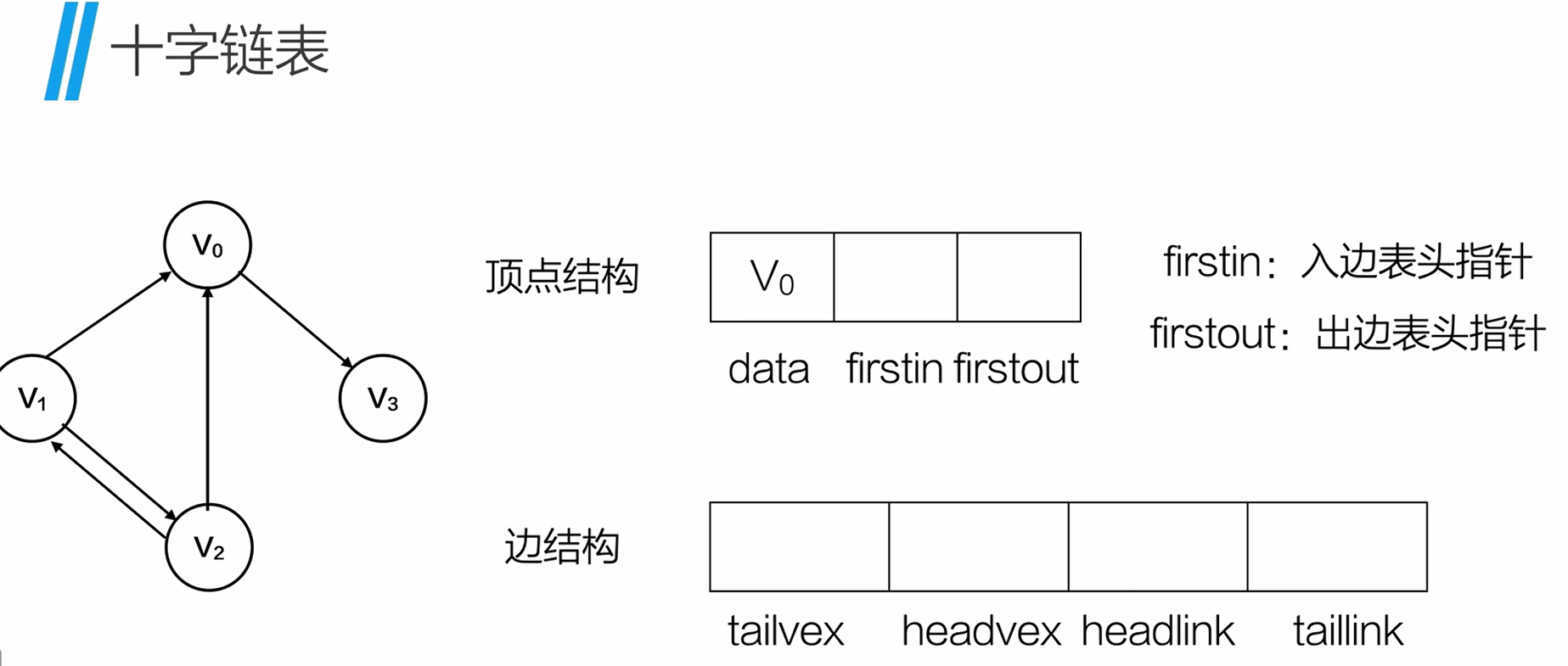
3.十字链表（有向图专用）

用于 有向图的链式表示，每条边都同时出现在：

  • 起点的出边链（tlink）

  • 终点的入边链（hlink）

优点

  • 可以 同时快速遍历入边与出边

  • 插入删除边方便

缺点

  • 结构较复杂

  • 不如邻接表直观

    typedef struct ArcNode {
    int tailvex; // 起点
    int headvex; // 终点
    struct ArcNode *hlink; // 入边链指针
    struct ArcNode *tlink; // 出边链指针
    } ArcNode;

    typedef struct VNode {
    char data; // 顶点存储（可改成 int）
    ArcNode *firstin; // 入边链的头指针
    ArcNode *firstout; // 出边链的头指针
    } VNode;

    typedef struct {
    VNode xList[100]; // 顶点数组
    int vexnum, arcnum; // 顶点数和边数
    } OLGraph;

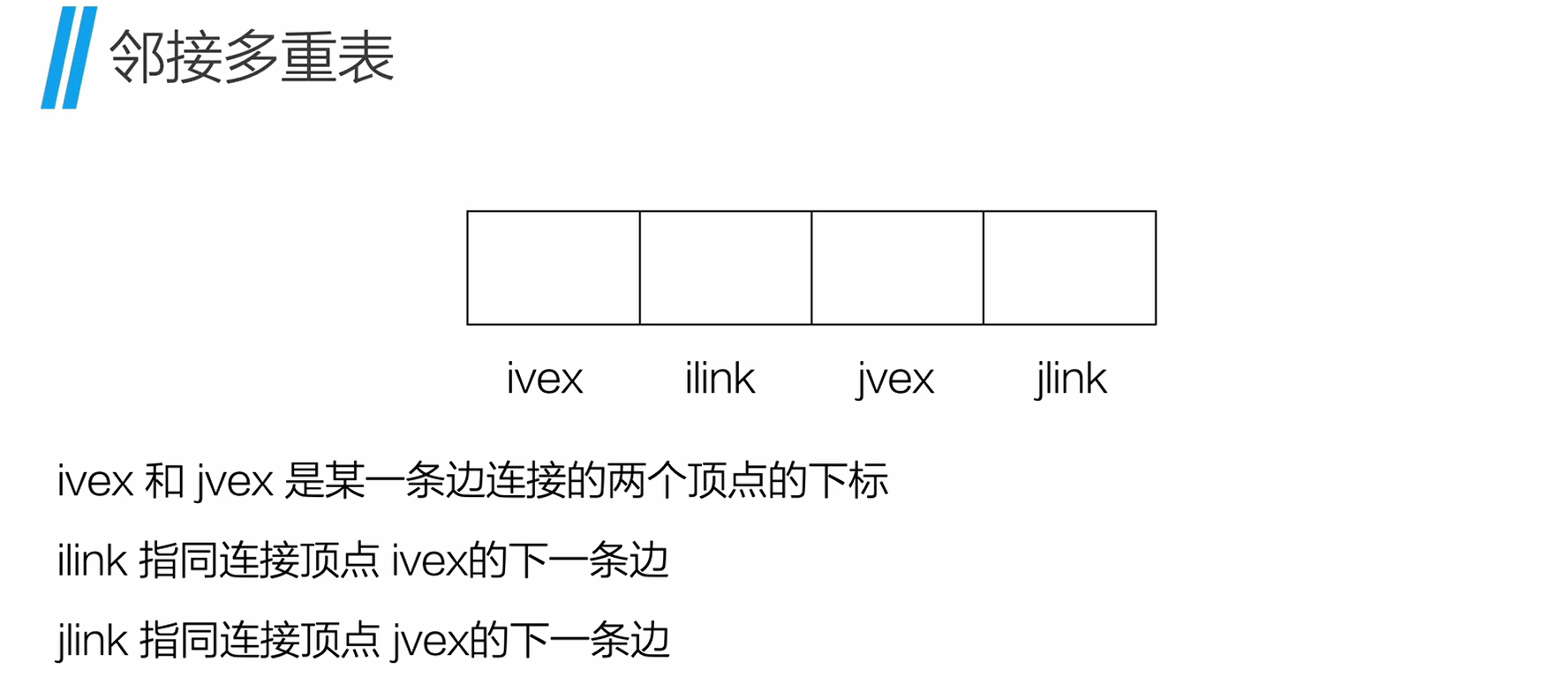
4.邻接多重表（无向图专用）

用于 无向图，每条边同时出现在两个顶点的边链中。

优点

  • 节省空间

  • 处理无向图边的遍历很方便

四、图的遍历

1、DFS（深度优先历）

一条路走到黑，再回头

复制代码 
#include <stdio.h>

#define MAX 100

int n;                  // 顶点个数
int G[MAX][MAX];        // 邻接矩阵
int visited[MAX];       // 访问标记数组

// 深度优先遍历
void DFS(int v) {
    printf("%d ", v);       // 访问当前顶点
    visited[v] = 1;

    // 按编号从小到大找相邻顶点（考试默认）
    for (int i = 0; i < n; i++) {
        if (G[v][i] != 0 && visited[i] == 0) {
            DFS(i);
        }
    }
}

int main() {
    int start;

    scanf("%d", &n);        // 输入顶点数

    // 输入邻接矩阵
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < n; j++) {
            scanf("%d", &G[i][j]);
        }
    }

    scanf("%d", &start);    // 起始顶点

    // 初始化访问数组
    for (int i = 0; i < n; i++) {
        visited[i] = 0;
    }

    DFS(start);

    return 0;
}

2.BFS（广度优先遍历）

一层一层往外走

复制代码 
#include <stdio.h>
#define MAX 100

int G[MAX][MAX];     // 邻接矩阵
int visited[MAX];    // 访问标记
int n;               // 顶点数

// 顺序队列
int queue[MAX];
int front = 0, rear = 0;

// 入队
void enqueue(int x) {
    queue[rear++] = x;
}

// 出队
int dequeue() {
    return queue[front++];
}

// 判断队列是否为空
int isEmpty() {
    return front == rear;
}

// 广度优先遍历
void BFS(int start) {
    printf("%d ", start);
    visited[start] = 1;
    enqueue(start);

    while (!isEmpty()) {
        int v = dequeue();

        // 按编号从小到大找相邻顶点
        for (int i = 0; i < n; i++) {
            if (G[v][i] != 0 && visited[i] == 0) {
                printf("%d ", i);
                visited[i] = 1;
                enqueue(i);
            }
        }
    }
}

int main() {
    int e;  // 边数
    scanf("%d %d", &n, &e);

    // 初始化邻接矩阵
    for (int i = 0; i < n; i++)
        for (int j = 0; j < n; j++)
            G[i][j] = 0;

    // 读入边
    for (int i = 0; i < e; i++) {
        int a, b;
        scanf("%d %d", &a, &b);
        G[a][b] = 1;
        G[b][a] = 1;   // 无向图
    }

    // 初始化 visited
    for (int i = 0; i < n; i++)
        visited[i] = 0;

    // 从 0 号顶点开始 BFS
    BFS(0);

    return 0;
}

五、最小生成树（MST）

在一个带权无向连通图中，选取 n−1 条边，使所有顶点连通，并且边权之和最小。

1.Prim 算法

从一个顶点出发，每次选择一条"连接已选顶点和未选顶点的最小权边"

(1)Prim 算法的时间复杂度：邻接矩阵实现：O(n²)，和起点无关，和边数无关.

(2) Prim = BFS + 最小权选择

（3）Prim 的过程

  1. 任选一个起点

  2. 已选集合 = {起点}

  3. 在"已选 → 未选"的所有边中

  4. 选 权值最小 的那一条

  5. 把新顶点加入

  6. 重复直到选够n−1 条边

    #include <stdio.h>
    #include <limits.h>

    #define MAXV 20
    #define MAX INT_MAX

    typedef struct {
    int vertex_num; // 顶点数
    char vertex[MAXV]; // 顶点信息（A、B、C...）
    int arc[MAXV][MAXV]; // 邻接矩阵（权值）
    } Graph;

    /* Prim 最小生成树算法 */
    void Prim(Graph *G, int start)
    {
    int weight[MAXV]; // 当前生成树到各顶点的最小边权
    int vex_index[MAXV]; // 记录最小边对应的起点

    复制代码 
     int min, i, j, k;

 /* 1. 初始化 */
 for (i = 0; i < G->vertex_num; i++)
 {
     weight[i] = G->arc[start][i];
     vex_index[i] = start;
 }

 /* 起点加入生成树 */
 weight[start] = 0;

 /* 2. 共选 vertex_num - 1 条边 */
 for (i = 1; i < G->vertex_num; i++)
 {
     min = MAX;
     j = 0;
     k = 0;

     /* 找当前最小的边 */
     while (j < G->vertex_num)
     {
         if (weight[j] != 0 && weight[j] < min)
         {
             min = weight[j];
             k = j;
         }
         j++;
     }

     /* 输出当前选中的边 */
     printf("(%c, %c)\n",
            G->vertex[vex_index[k]],
            G->vertex[k]);

     /* 将顶点 k 加入生成树 */
     weight[k] = 0;

     /* 更新 weight 数组 */
     for (j = 0; j < G->vertex_num; j++)
     {
         if (weight[j] != 0 && G->arc[k][j] < weight[j])
         {
             weight[j] = G->arc[k][j];
             vex_index[j] = k;
         }
     }
 }

    }

    /* 测试用 main（考试可不要） */
    int main()
    {
    Graph G = {
    5,
    {'A','B','C','D','E'},
    {
    {0, 2, MAX, 6, MAX},
    {2, 0, 3, 8, 5},
    {MAX, 3, 0, MAX, 7},
    {6, 8, MAX, 0, 9},
    {MAX, 5, 7, 9, 0}
    }
    };

    复制代码 
     Prim(&G, 0);   // 从 A 开始
 return 0;

    }

2.Kruskal 算法

把所有边按权值从小到大排序，能加就加，但不能形成回路

Kruskal 的过程（贪心 + 排序）

  1. 所有边按权值排序

  2. 依次取最小的边

  3. 如果 不形成回路 → 加入

  4. 否则跳过

  5. 直到边数 = n−1

    #include <stdio.h>

    #define MAXV 20 // 最大顶点数
    #define MAXE 50 // 最大边数
    #define INF 100000 // 表示无穷大

    /* 边的结构体 */
    typedef struct {
    int u; // 边的一个端点
    int v; // 边的另一个端点
    int w; // 边的权值
    } Edge;

    /* 并查集数组 */
    int parent[MAXV];

    /* 并查集：查找根节点 */
    int find(int x)
    {
    while (parent[x] != x)
    x = parent[x];
    return x;
    }

    /* 并查集：合并两个集合 */
    void unite(int x, int y)
    {
    int fx = find(x);
    int fy = find(y);
    if (fx != fy)
    parent[fx] = fy;
    }

    /* 按边权从小到大排序（冒泡，考试够用） */
    void sortEdges(Edge edges[], int m)
    {
    for (int i = 0; i < m - 1; i++)
    {
    for (int j = 0; j < m - 1 - i; j++)
    {
    if (edges[j].w > edges[j + 1].w)
    {
    Edge temp = edges[j];
    edges[j] = edges[j + 1];
    edges[j + 1] = temp;
    }
    }
    }
    }

    /* Kruskal 最小生成树算法 */
    void Kruskal(Edge edges[], int n, int m)
    {
    int count = 0; // 已选边数
    int sum = 0; // 最小生成树权值和

    复制代码 
     /* 1️⃣ 初始化并查集 */
 for (int i = 0; i < n; i++)
     parent[i] = i;

 /* 2️⃣ 对所有边按权值排序 */
 sortEdges(edges, m);

 /* 3️⃣ 依次选边 */
 for (int i = 0; i < m && count < n - 1; i++)
 {
     int u = edges[i].u;
     int v = edges[i].v;
     int w = edges[i].w;

     /* 如果两个端点不在同一集合，则不会形成回路 */
     if (find(u) != find(v))
     {
         unite(u, v);   // 合并集合
         count++;       // 已选边数 +1
         sum += w;      // 累加权值

         printf("选中边：(%d, %d)，权值 = %d\n", u, v, w);
     }
 }

 printf("最小生成树的总权值 = %d\n", sum);

    }

    int main()
    {
    /* 图中共有 5 个顶点，7 条边 */
    Edge edges[MAXE] = {
    {0, 1, 2},
    {0, 3, 6},
    {1, 2, 3},
    {1, 3, 8},
    {1, 4, 5},
    {2, 4, 7},
    {3, 4, 9}
    };

    复制代码 
     int n = 5;  // 顶点数
 int m = 7;  // 边数

 Kruskal(edges, n, m);

 return 0;

    }

六、最短路径

在带权图中，找从一个顶点到另一个顶点（或所有顶点）的路径，使得路径总权值最小。

① BFS（无权图最短路径）

② Dijkstra 算法

复制代码 
#include <stdio.h>

#define MAX 100
#define INF 1000000000

int n;                 // 顶点数
int G[MAX][MAX];       // 邻接矩阵
int dist[MAX];         // 起点到各点的最短距离
int visited[MAX];      // 是否已确定最短路径

void dijkstra(int start) {
    // 1️⃣ 初始化
    for (int i = 0; i < n; i++) {
        dist[i] = G[start][i]; // 起点到各点的初始距离
        visited[i] = 0;        // 都没访问过
    }
    dist[start] = 0;           // 起点到自己是 0
    visited[start] = 1;        // 起点先确定

    // 2️⃣ 重复 n-1 次
    for (int i = 1; i < n; i++) {
        int min = INF;
        int u = -1;

        // 找当前 未访问 且 dist 最小的点
        for (int j = 0; j < n; j++) {
            if (!visited[j] && dist[j] < min) {
                min = dist[j];
                u = j;
            }
        }

        if (u == -1) return;   // 剩下的点不可达

        visited[u] = 1;        // u 的最短路径确定

        // 用 u 去更新它的邻接点
        for (int v = 0; v < n; v++) {
            if (!visited[v] && G[u][v] < INF) {
                if (dist[u] + G[u][v] < dist[v]) {
                    dist[v] = dist[u] + G[u][v];
                }
            }
        }
    }
}

int main() {
    scanf("%d", &n);

    // 输入邻接矩阵
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < n; j++) {
            scanf("%d", &G[i][j]);
            if (G[i][j] == 0 && i != j)
                G[i][j] = INF; // 0 表示无边（非自己）
        }
    }

    dijkstra(0);  // 从 0 号顶点出发

    // 输出结果
    for (int i = 0; i < n; i++) {
        printf("0 -> %d : %d\n", i, dist[i]);
    }

    return 0;
}

③ Floyd 算法（多源最短路径）

复制代码 
#include <stdio.h>

#define MAX 100
#define INF 1000000000

int n;
int dist[MAX][MAX];

void floyd() {
    // 三层循环，k 一定在最外层
    for (int k = 0; k < n; k++) {
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                if (dist[i][k] + dist[k][j] < dist[i][j]) {
                    dist[i][j] = dist[i][k] + dist[k][j];
                }
            }
        }
    }
}

int main() {
    scanf("%d", &n);

    // 输入邻接矩阵
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < n; j++) {
            scanf("%d", &dist[i][j]);
            if (dist[i][j] == 0 && i != j)
                dist[i][j] = INF;
        }
    }

    floyd();

    // 输出任意两点最短路径
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < n; j++) {
            printf("%d ", dist[i][j]);
        }
        printf("\n");
    }

    return 0;
}

七、拓扑排序

对一个有向无环图中的顶点进行排序，使得每一条有向边 u → v 中，u 都排在 v 的前面。
**不断选择"入度为 0 的顶点"，输出它，并删除它的出边（**入度 = 指向该顶点的边的条数）

为什么要找"入度为 0"的点？它没有任何前置依赖，可以最先做

为什么删除出边？"这个任务完成了，它对后面的限制解除"

为什么能判断是否有环？如果有环：环中的点 **入度永远不为 0，**永远进不了队列

复制代码 
#include <stdio.h>

#define MAX 100

int n;
int G[MAX][MAX];
int indegree[MAX];     // 入度数组
int queue[MAX];        // 模拟队列
int front = 0, rear = 0;

void topo_sort() {
    // 1️⃣ 初始化入度
    for (int i = 0; i < n; i++) {
        indegree[i] = 0;
    }

    // 统计入度
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < n; j++) {
            if (G[i][j] != 0) {
                indegree[j]++;
            }
        }
    }

    // 2️⃣ 入度为 0 的点入队
    for (int i = 0; i < n; i++) {
        if (indegree[i] == 0) {
            queue[rear++] = i;
        }
    }

    int count = 0;  // 记录输出的顶点数

    // 3️⃣ 拓扑排序过程
    while (front < rear) {
        int u = queue[front++];
        printf("%d ", u);
        count++;

        // 删除 u 的所有出边
        for (int v = 0; v < n; v++) {
            if (G[u][v] != 0) {
                indegree[v]--;
                if (indegree[v] == 0) {
                    queue[rear++] = v;
                }
            }
        }
    }

    // 4️⃣ 判断是否有环
    if (count < n) {
        printf("\n图中存在环，无法拓扑排序\n");
    }
}
相关推荐
无限进步_2 小时前
【C语言&数据结构】有效的括号：栈数据结构的经典应用
c语言·开发语言·数据结构·c++·git·github·visual studio
专注API从业者3 小时前
构建企业级 1688 数据管道：商品详情 API 的分布式采集与容错设计
大数据·开发语言·数据结构·数据库·分布式
天赐学c语言4 小时前
12.20 - 反转链表II && 传值和传地址的区别
数据结构·c++·算法·链表·leecode
良木生香4 小时前
【诗句结构-初阶】详解栈和队列(2)---队列
c语言·数据结构·算法·蓝桥杯
聆风吟º4 小时前
【数据结构手札】顺序表实战指南（二）：结构体构建 | 初始化 | 打印 | 销毁
数据结构·初始化顺序表·销毁顺序表·打印顺序表
量子炒饭大师4 小时前
Cyber骇客的LIFO深渊与FIFO管道 ——【初阶数据结构与算法】栈与队列
c语言·数据结构·c++·链表
一起养小猫4 小时前
LeetCode100天Day3-判断子序列与汇总区间
java·数据结构·算法·leetcode
404未精通的狗4 小时前
（数据结构）二叉树、二叉搜索树+简单的排序算法（考前速成版）
数据结构·算法·排序算法
太理摆烂哥4 小时前
数据结构之并查集
数据结构
热门推荐
01GitHub 镜像站点02UV安装并设置国内源03Linux下V2Ray安装配置指南04BongoCat - 跨平台键盘猫动画工具05jdk21下载、安装（Windows、Linux、macOS）06在VSCode配置Java开发环境的保姆级教程（适配各类AI编程IDE）07安娜的档案(Anna’s Archive) 镜像网站/国内最新可访问入口（持续更新）08sqli-labs靶场通关笔记：第18-19关 HTTP头部注入09Open-AutoGLM Windows 安装部署教程10RedissonClient的配置解析