探索Matlab/simulink永磁同步电机在线惯量辨识模型：基于遗忘因子的递归最小二乘法

Matlab/simulink永磁同步电机在线惯量辨识模型，基于遗忘因子的递归最小二乘法。表贴式永磁同步电机可以准确辨识转动惯量j，阻尼系数b，电感以及磁链等。有资料，基于sfunction写的，有注释，很容易看懂，

在电机控制领域，准确获取永磁同步电机（PMSM）的各项参数至关重要，尤其是转动惯量 \( J \) 和阻尼系数 \( b \) 等。今天咱们就来聊聊基于Matlab/simulink的永磁同步电机在线惯量辨识模型，这里用到的核心算法是基于遗忘因子的递归最小二乘法。

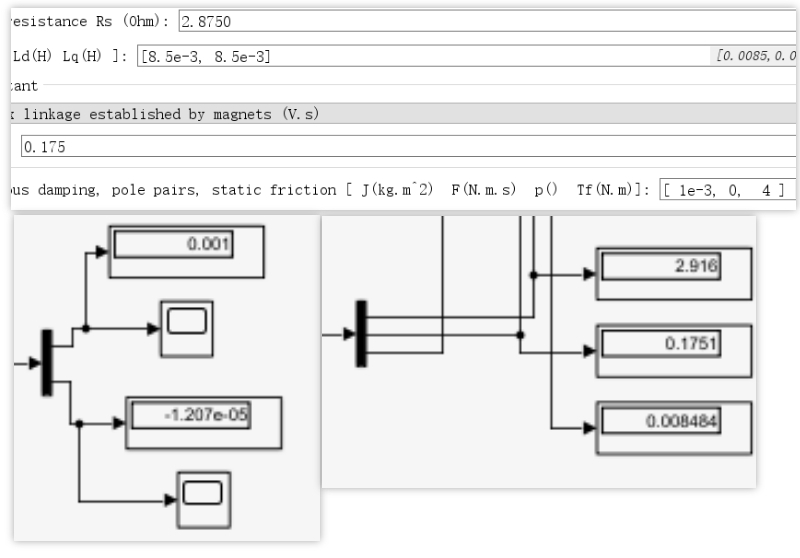
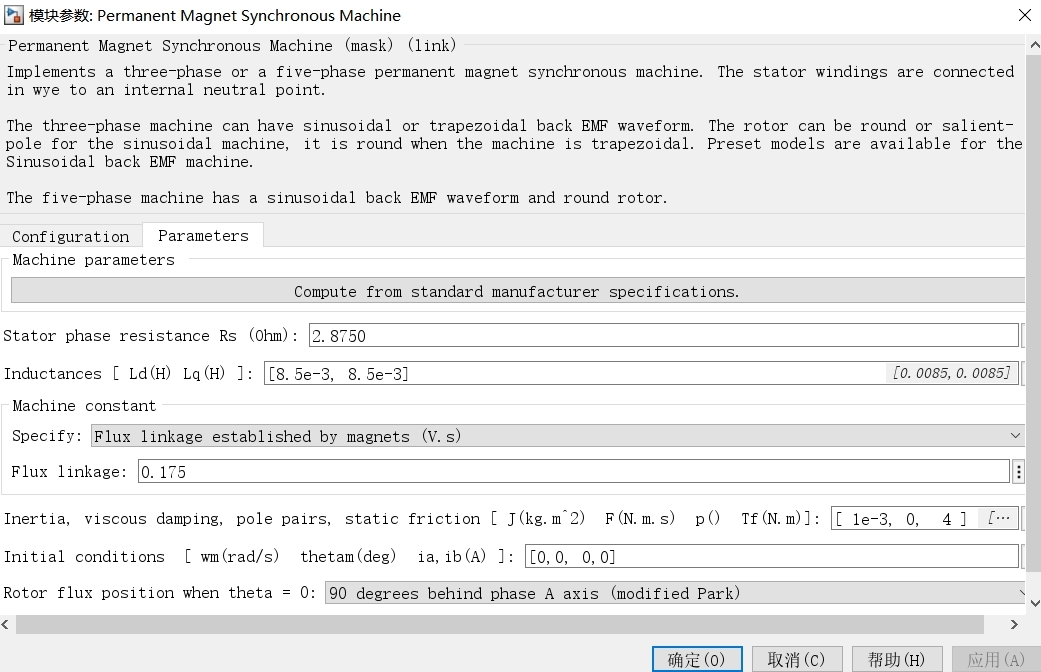
咱们先看看表贴式永磁同步电机（SPMSM）。它结构相对简单，在很多高性能伺服系统中应用广泛。对它的参数准确辨识，能大大提升控制系统的性能。像转动惯量 \( J \) ，它影响着电机的动态响应速度，阻尼系数 \( b \) 则和系统的稳定性息息相关。不仅如此，电感以及磁链的准确辨识同样重要，它们对电机的电磁转矩计算和磁场定向控制起着关键作用。

基于遗忘因子的递归最小二乘法原理

遗忘因子的递归最小二乘法，简单说就是在传统递归最小二乘法基础上，给旧数据加上一个逐渐衰减的权重，这样能让算法更关注新数据，适应时变系统。

假设我们有一个线性回归模型 \( y(k)=\boldsymbol{\varphi}^T(k)\boldsymbol{\theta}+v(k) \) ，这里 \( y(k) \) 是输出， \( \boldsymbol{\varphi}(k) \) 是回归向量， \( \boldsymbol{\theta} \) 是待估计参数向量， \( v(k) \) 是噪声。

递归最小二乘法递推公式如下：

matlab 复制代码

% 初始化参数
P = eye(n); % P矩阵初始化，n是待估计参数个数
theta_hat = zeros(n,1); % 初始估计参数向量
lambda = 0.98; % 遗忘因子，接近1表示对旧数据遗忘慢

for k = 1:N % N是数据长度
    phi = [y(k-1); u(k-1)]; % 假设回归向量由输出和输入延迟组成
    K = P*phi/(lambda + phi'*P*phi); % 增益矩阵
    theta_hat = theta_hat + K*(y(k) - phi'*theta_hat); % 更新估计参数
    P = (1/lambda)*(P - K*phi'*P); % 更新P矩阵
end

在上述代码里， lambda 就是遗忘因子。如果 lambda 接近1，算法对旧数据依赖程度高，适应变化慢；要是 lambda 小，新数据影响大，能快速跟踪变化，但可能对噪声敏感。

基于S - function实现永磁同步电机参数辨识

资料里基于S - function实现的模型很贴心地加了注释，容易理解。S - function是Matlab/Simulink里一个强大工具，能自定义系统模块。

下面简单示意下S - function框架（以辨识转动惯量为例，代码有简化）：

matlab 复制代码

function [sys,x0,str,ts] = pmsm_id_sfunc(t,x,u,flag)
switch flag,
    case 0,
        [sys,x0,str,ts]=mdlInitializeSizes; % 初始化模块大小等参数
    case 1,
        sys=mdlDerivatives(t,x,u); % 计算连续状态的导数（这里可能没用）
    case 2,
        sys=mdlUpdate(t,x,u); % 更新离散状态
    case 3,
        sys=mdlOutputs(t,x,u); % 计算输出，这里可以输出辨识的转动惯量J
    case 4,
        sys=mdlGetTimeOfNextVarHit(t,x,u); % 计算下一次采样时间
    case 9,
        sys=mdlTerminate(t,x,u); % 结束仿真时执行
    otherwise
        sys = [];
end

在 mdlOutputs 函数里，可以把基于遗忘因子递归最小二乘法得到的转动惯量 \( J \) 输出。

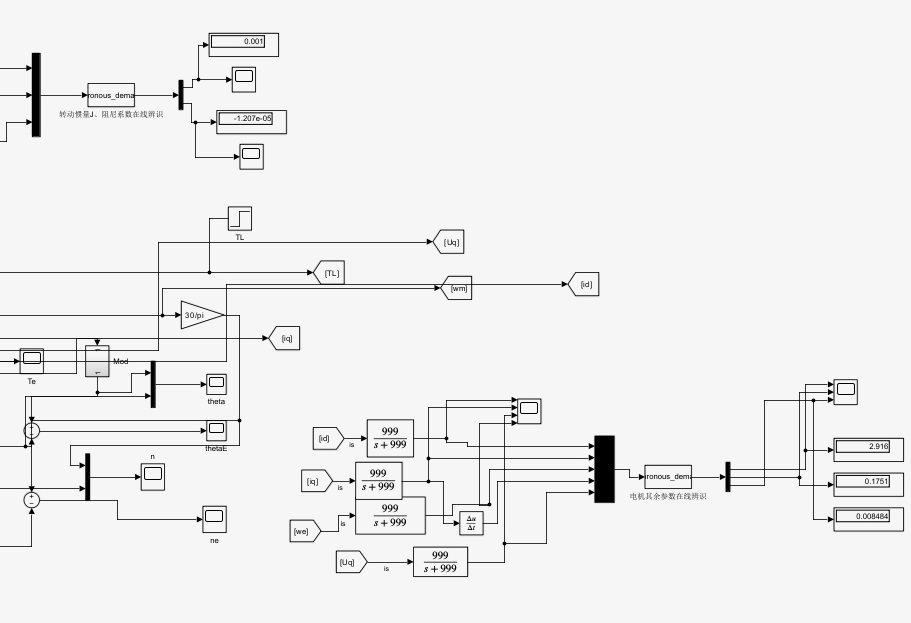
通过这样的基于S - function实现的永磁同步电机在线惯量辨识模型，利用遗忘因子的递归最小二乘法，我们就能够较为准确地辨识出转动惯量 \( J \) 、阻尼系数 \( b \) 、电感以及磁链等重要参数，为永磁同步电机的高性能控制打下坚实基础。无论是在工业驱动还是航空航天等对电机性能要求极高的领域，这样的参数辨识方法都有着广阔的应用前景。