1. 引言
本文不涉及那些高深而抽象的物理学知识,而是以袜子为例,来形象解释量子纠缠的概念。
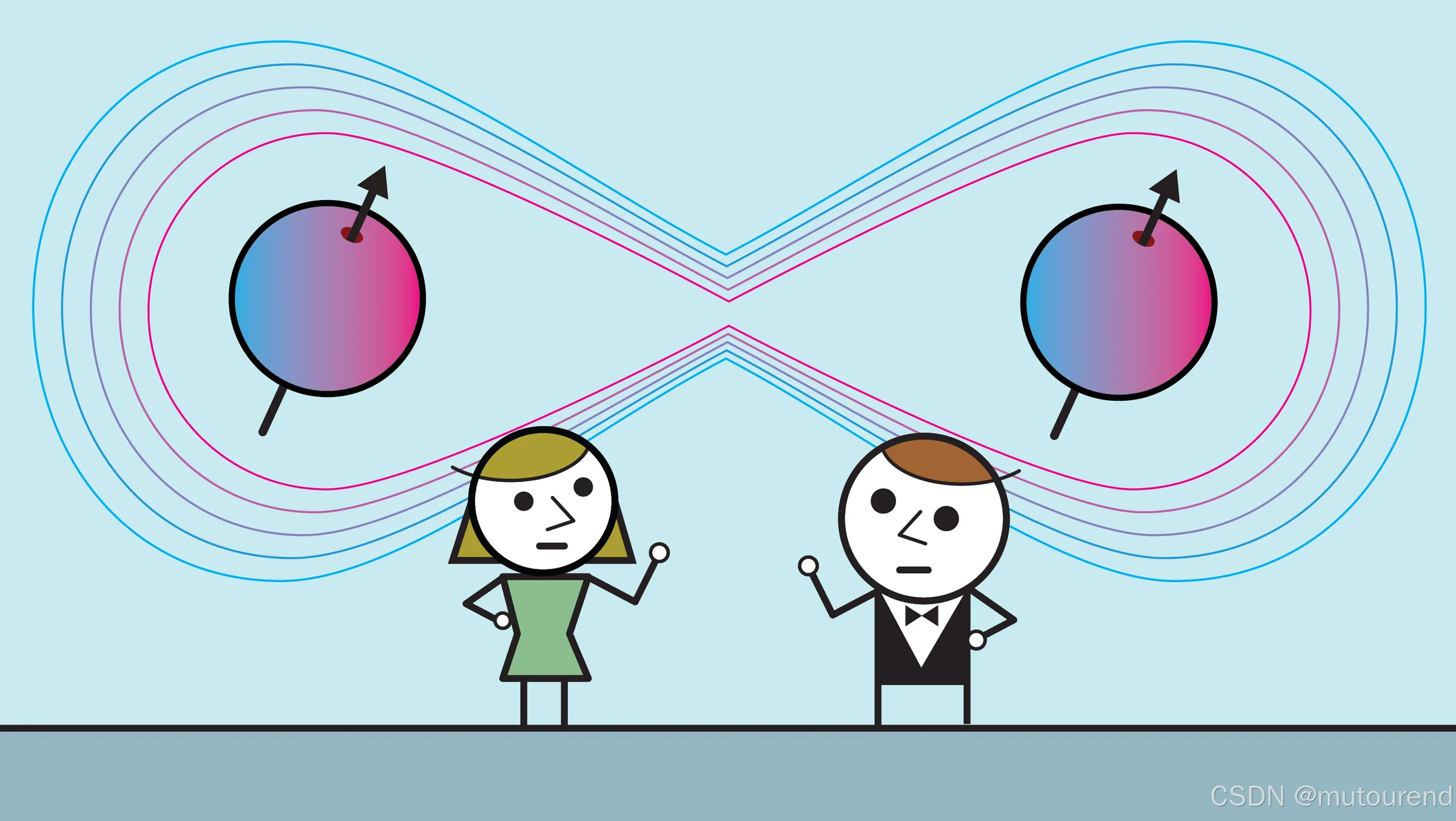
当被要求解释为什么量子计算机能够比经典计算机更快时,关于量子计算的故事往往会提到一种神秘的性质,称为"纠缠(entanglement)"。读者通常会被告知,量子比特可以以某种方式在量子力学意义上发生纠缠 ,从而彼此依赖。如果还需要更多细节,读者会听到这样的说法:纠缠能够将量子比特联系在一起,无论它们相距多远------只要这些量子比特保持"相干"。
然而,对读者来说,这些解释一点也不"相干"。当然,纠缠是量子计算中的一个重要方面,但它究竟是什么?
简单来说,纠缠指的是多个物体------如一对电子或光子------共享同一个量子态。就像一团缠在一起的毛线中的线头一样,处于纠缠状态的物体无法被描述为彼此独立的个体。
这个解释或许富有诗意,但并不足以令人满意。事情并没有那么简单或直观。不过,只需要一点高中水平的数学(在本文接近结尾处),基于人们一生经典物理经验所形成的直觉,就可以被稍微重新训练和引导。
当然,也需要先作出如下声明:
- 任何简短的解释都无法全面传达量子力学的完整内涵。
本人的目标只是阐明纠缠背后的基本概念,让读者能够更深入地理解这一量子计算基础现象背后究竟发生了什么。
从著名的北爱尔兰物理学家 约翰·斯图尔特·贝尔(John Stewart Bell) 的一个稍作修改的例子开始:
- 爱丽丝(Alice)和鲍勃(Bob)都知道,伯特尔曼教授(Prof. Bertlmann)总是穿着不成对的袜子。如果他的左脚袜子是粉色的,那么他的右脚袜子就一定不是粉色。(本文的插图大致参考了贝尔本人为解释纠缠而绘制的漫画,这些漫画描绘的是他的朋友赖因霍尔德·伯特尔曼(Reinhold Bertlmann),最初发表于他在 1980 年的Bertlmann's socks and the nature of reality文章 中。)
如下图所示的伯特尔曼教授------他那可预测、也始终如一的不成对袜子:

爱丽丝和鲍勃想要测试一下,伯特尔曼教授在课堂之外是否仍然保持这样的穿袜习惯,于是他们决定暗中观察他。
假设爱丽丝站在一个街区之外,她看到伯特尔曼教授左脚的袜子是蓝色的。她立刻就知道,正在观察伯特尔曼右脚袜子的鲍勃一定会看到粉色。即便爱丽丝远在光年之外,通过望远镜观察伯特尔曼的穿着情况,这一点依然成立。一旦爱丽丝测量了其中一只袜子的颜色,她就会瞬间知道鲍勃将会在另一只袜子上测量到什么。这是因为,这一双不成对的袜子在物理学家(以及过度专业的服装顾问)看来是彼此相关联 (correlated)的。
如下图所示,爱丽丝看到伯特尔曼教授的右脚袜子是蓝色;鲍勃则看到他的左脚袜子是粉色:
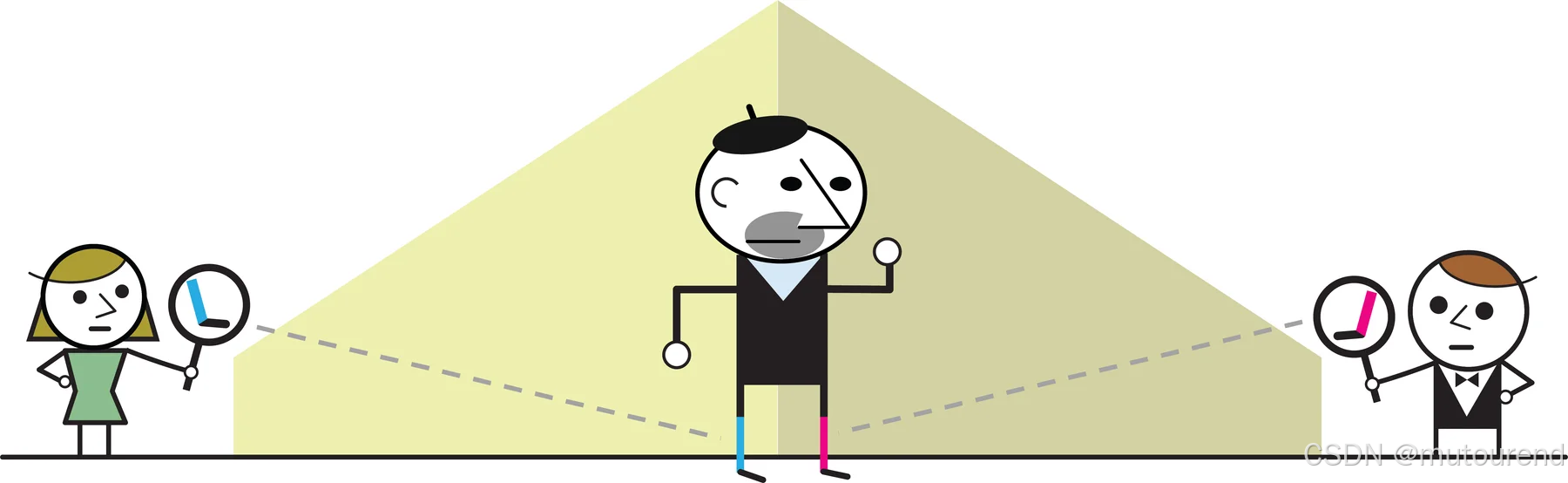
这种相关性是如何产生的,其实一点也不神秘:每天早晨,伯特尔曼教授都会刻意把袜子穿成不成对的样子。如果他左脚穿的是蓝色袜子,那么他就会给右脚穿上一只粉色袜子。这种相关性具有三个经典特征:它们是真实的 、局域的 ,并且是确定性的 。
真实(Real) :在爱丽丝或鲍勃进行测量之前,袜子就已经具有确定的颜色。
确定性(Deterministic) :袜子的颜色并非随机产生。在完全相同的初始条件下(如星期几、是否有下雨的可能、脚趾是否疼痛),伯特尔曼教授会以同样的方式穿上那双不成对的袜子。
注意:虽然爱丽丝和鲍勃可能很难预测每只脚具体会穿什么颜色,但这一过程本身并不是严格随机的。
局域性(Local):袜子的颜色只取决于其周围的局部环境------也就是说,鲍勃看到什么不应该依赖于爱丽丝的测量结果。
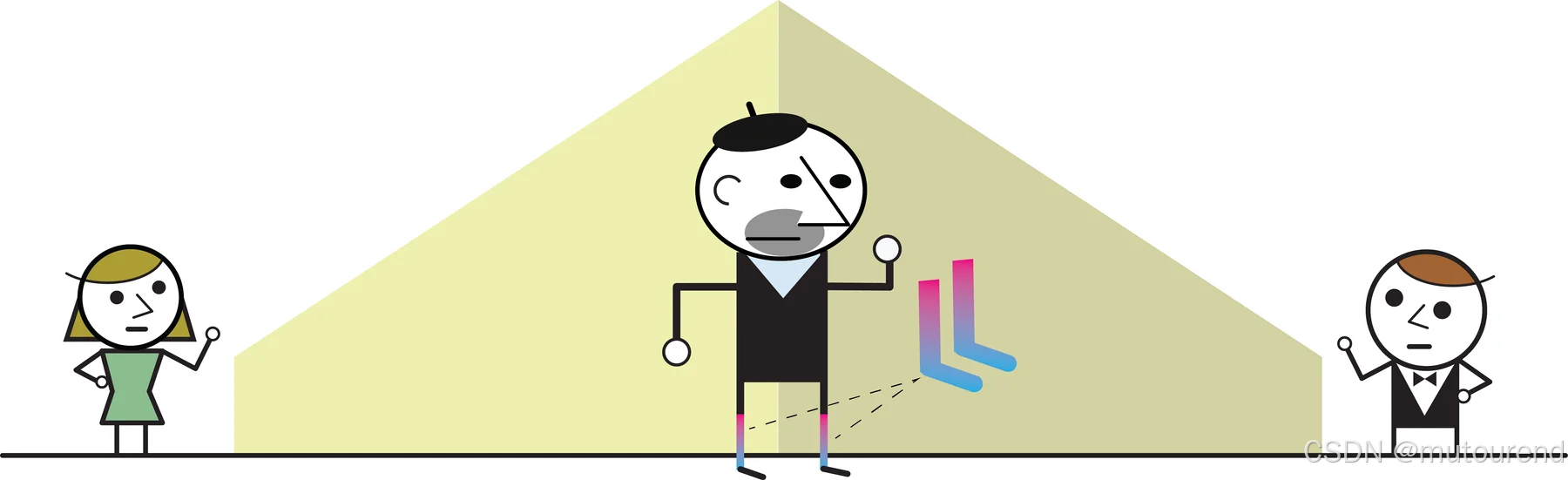
现在,假设伯特尔曼教授想要给这些偷偷观察他的学生上一堂关于纠缠的课。第二天早上,他穿上了一双不成对的量子袜子,而这双袜子的颜色是彼此纠缠的。
如下图所示,伯特尔曼教授通过引入量子袜子让情况变得更加复杂------这种袜子的颜色在被观测之前是不确定的:
当爱丽丝测量左脚袜子时,这一对袜子原本不确定的颜色状态发生塌缩,使得爱丽丝看到的结果要么是粉色,要么是蓝色:
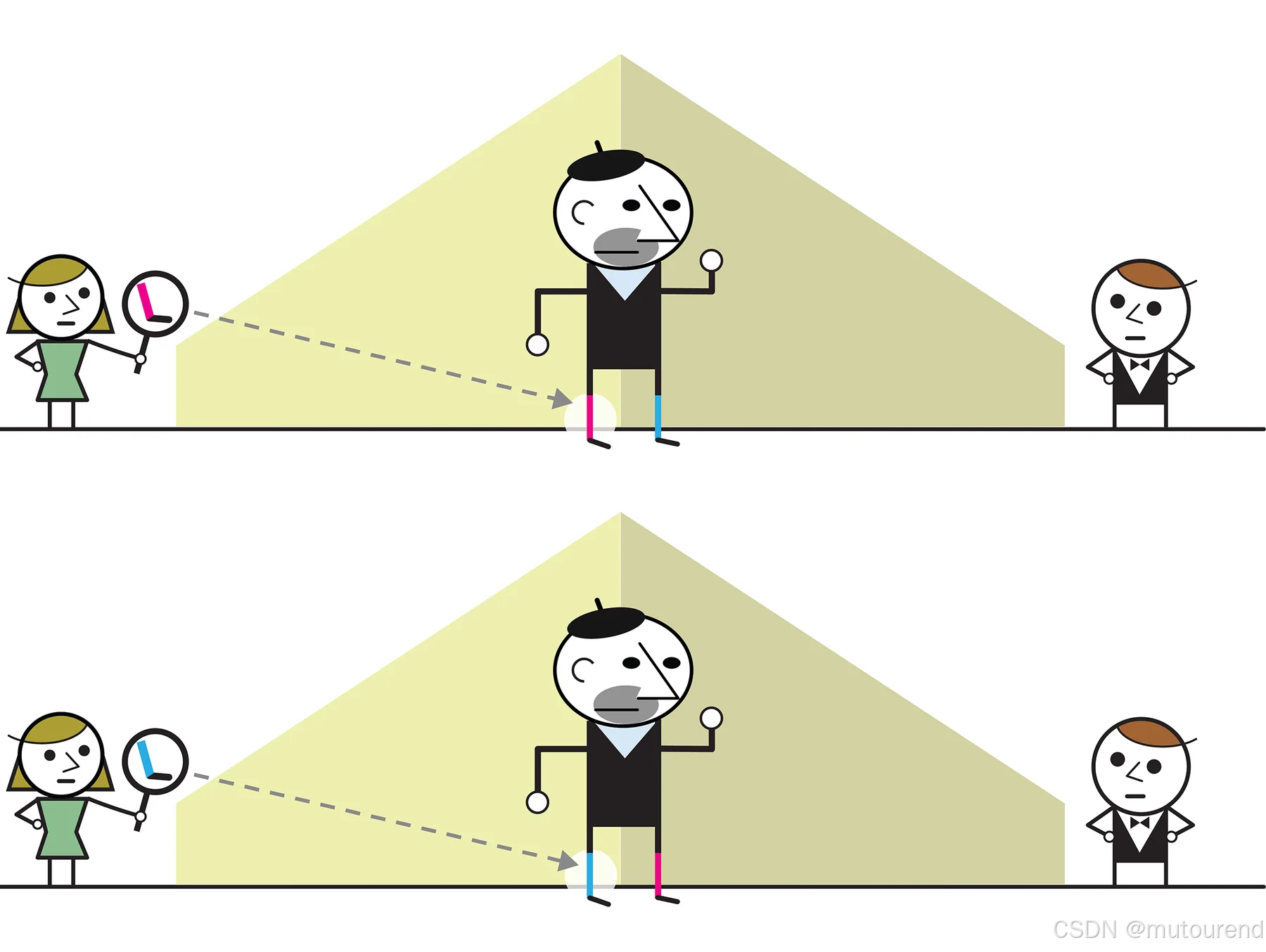
与他的经典袜子不同,伯特尔曼教授的纠缠量子袜子具有以下特性:
非真实(Unreal) :在测量之前,袜子并没有确定的颜色。
非确定性(Nondeterministic) :袜子的颜色是随机的。在完全相同的初始条件下进行测量,结果仍然不可预测------如,有 50% 的概率袜子是粉色,50% 的概率是蓝色。
非局域性(Nonlocal):每只袜子的颜色取决于非局域的环境------也就是说,鲍勃看到的结果取决于爱丽丝的测量。
在量子情形下,如果爱丽丝测量了其中一只袜子的颜色,她的测量会瞬间更新另一只此前颜色不确定的袜子的状态。(注意:由于袜子的颜色本身是随机的,这种更新并不会严格意义上传递信息------因此也不能用于超光速通信。)
不过,爱丽丝提出了异议:这些袜子离得很近------难道它们不能彼此发送某种信号吗?这种更新真的会是瞬时的吗?为了进一步说服学生们这里确实存在某种非局域现象,伯特尔曼教授将两只袜子分别送往相距数光年的遥远恒星。
如下图所示,现在,这位教授传奇般的量子袜子已经被分别送往不同的恒星系统,彼此相距数光年:

与之前一样,当爱丽丝观测左脚袜子时,这一对袜子原本不确定的颜色状态发生塌缩,这个测量会瞬间更新另一只袜子的颜色:

为简单起见,只展示了爱丽丝进行测量的情形,但如果鲍勃也进行测量,结果并不会发生变化:

随后,伯特尔曼教授让爱丽丝和鲍勃进行同样的实验。
结果再次表明,鲍勃所看到的结果取决于爱丽丝的测量,尽管袜子之间根本不可能进行任何通信。这个结果理应令人震惊。正如伯特尔曼教授所说:
- "为什么它们在被观察时总是选择不同的颜色?第二只袜子是怎么知道第一只做了什么的?"
持怀疑态度的学生爱丽丝和鲍勃对伯特尔曼教授所谓"纠缠"的袜子并不买账。在他们看来,"幽灵般"的袜子与隐藏变量袜子在实验上没有任何区别:两者看起来都会在测量时相互更新,但按照隐藏变量理论,袜子的颜色其实早已注定。
为了让这些不太信服的学生真正理解纠缠的本质,伯特尔曼教授设计了一个新的实验:
- 在这个实验中,爱丽丝和鲍勃分别乘坐宇宙飞船远离地球。一处源头向他们发射成对的纠缠量子袜子。爱丽丝和鲍勃各自配备了带有两种设置的特殊探测器。爱丽丝的探测器可以设置为 A 或 a;鲍勃的探测器可以设置为 B 或 b。(为了选择设置,他们会在袜子发射之后各自抛硬币,因此袜子不可能事先知道探测器的设置。)
如下图所示,为了避免任何可能的局域效应,爱丽丝和鲍勃飞到彼此相距数光年的位置。他们需要这种隔离,以判断袜子的颜色究竟是预先决定的,还是在测量时才真正发生更新。
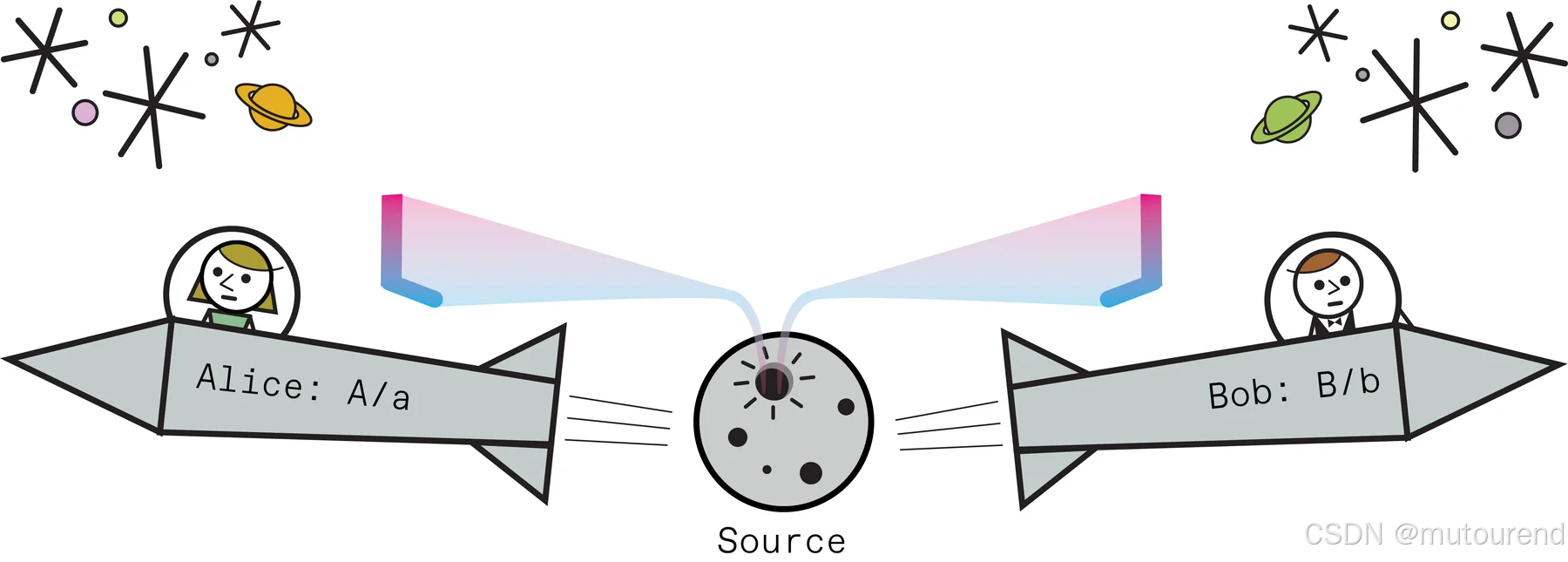
当爱丽丝和鲍勃使用不同的设置(a 与 B,或 A 与 b)时,袜子有时匹配,有时不匹配。
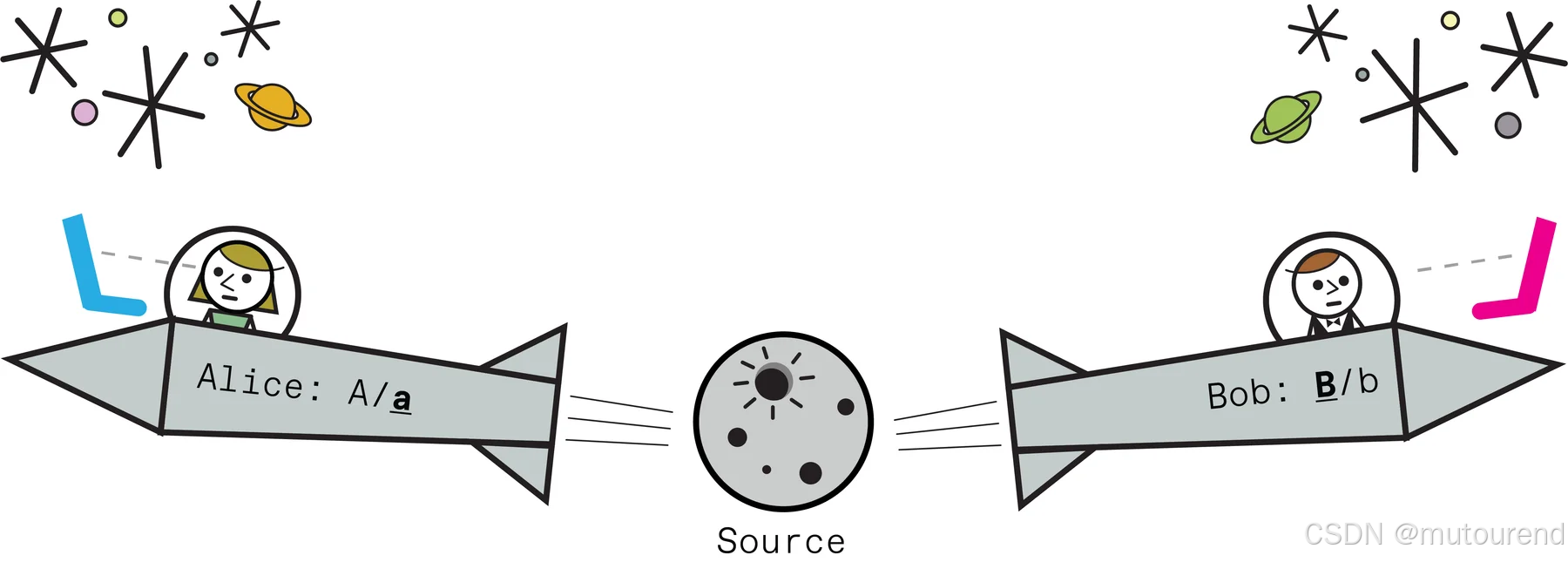
当爱丽丝和鲍勃使用相同的设置(A 与 B,或 a 与 b)时,袜子总是匹配。如果抛硬币是在袜子发射之后才发生的,那么预先决定颜色的袜子又是如何做到这种相关性的呢?
下面是爱丽丝和鲍勃得到的一组示例输出结果:
| ALICE | BOB |
|---|---|
| 🩷 P | 🩵 B |
| 🩵 B | 🩵 B |
| 🩵 B | 🩵 B |
| 🩵 B | 🩵 B |
| 🩵 B | 🩷 P |
| 🩵 B | 🩵 B |
| 🩷 P | 🩷 P |
| 🩷 P | 🩵 B |
| 🩵 B | 🩷 P |
| 🩵 B | 🩵 B |
| 🩵 B | 🩷 P |
| 🩷 P | 🩷 P |
| 🩵 B | 🩵 B |
| 🩷 P | 🩵 B |
| 🩵 B | 🩵 B |
| 🩵 B | 🩵 B |
| 🩷 P | 🩷 P |
| 🩷 P | 🩷 P |
由上可知,爱丽丝和鲍勃测量到的颜色是随机的。现在,把同样是随机选择的探测器设置也加入进来:
| 设置 | Alice | 设置 | Bob |
|---|---|---|---|
| A | 🩷 P | b | 🩵 B |
| A | 🩵 B | B | 🩵 B |
| a | 🩵 B | b | 🩵 B |
| A | 🩵 B | B | 🩵 B |
| a | 🩵 B | B | 🩷 P |
| a | 🩵 B | b | 🩵 B |
| A | 🩷 P | B | 🩷 P |
| A | 🩷 P | b | 🩵 B |
| a | 🩷 P | B | 🩷 P |
| A | 🩵 B | B | 🩵 B |
| a | 🩵 B | B | 🩷 P |
| a | 🩷 P | b | 🩷 P |
| a | 🩵 B | b | 🩵 B |
| A | 🩷 P | b | 🩵 B |
| A | 🩵 B | B | 🩵 B |
| a | 🩵 B | B | 🩵 B |
| A | 🩷 P | b | 🩷 P |
| a | 🩷 P | B | 🩷 P |
从表中可以看出,当爱丽丝和鲍勃使用不同的设置时,袜子有时匹配,有时不匹配;但如果爱丽丝和鲍勃使用相同的设置(两者都是大写或两者都是小写),它们总是匹配。仿佛在袜子发射之后、爱丽丝和鲍勃才抛硬币选择设置的情况下,这些袜子仍然能够在跨越巨大距离时"彼此沟通",决定何时匹配。这种现象非常奇怪------就好像袜子的颜色是预先决定好的一样!
在爱丽丝和鲍勃记录完所有数据之后,他们回到地球。伯特尔曼教授解释说,这种奇怪的巧合还不足以揭示纠缠的真实本质。他们需要测量袜子之间的相关程度,于是爱丽丝和鲍勃建立了一张新的表格,将粉色记为 −1,将蓝色记为 +1。
| 设置 | Alice | 设置 | Bob | 组合设置 | 和 |
|---|---|---|---|---|---|
| A | 🩷 −1 | b | 🩵 +1 | Ab | 0 |
| A | 🩵 +1 | B | 🩵 +1 | AB | 2 |
| a | 🩵 +1 | b | 🩵 +1 | ab | 2 |
| A | 🩵 +1 | B | 🩵 +1 | AB | 2 |
| a | 🩵 +1 | B | 🩷 −1 | aB | 0 |
| a | 🩵 +1 | b | 🩵 +1 | ab | 2 |
| A | 🩷 −1 | B | 🩷 −1 | AB | −2 |
| A | 🩷 −1 | b | 🩵 +1 | Ab | 0 |
| a | 🩷 −1 | B | 🩷 −1 | aB | −2 |
| A | 🩵 +1 | B | 🩵 +1 | AB | 2 |
| a | 🩵 +1 | B | 🩷 −1 | aB | 0 |
| a | 🩷 −1 | b | 🩷 −1 | ab | −2 |
| a | 🩵 +1 | b | 🩵 +1 | ab | 2 |
| A | 🩷 −1 | b | 🩵 +1 | Ab | 0 |
| A | 🩵 +1 | B | 🩵 +1 | AB | 2 |
| a | 🩵 +1 | B | 🩵 +1 | aB | 2 |
| A | 🩷 −1 | b | 🩷 −1 | Ab | −2 |
| a | 🩷 −1 | B | 🩷 −1 | aB | −2 |
"有一个非常简单的证明------可以自己去验证------它表明:如果袜子颜色真的服从隐藏变量理论,那么 |AB − Ab + aB + ab| 的绝对值不可能大于 2。"伯特尔曼教授解释道。
通过统计,爱丽丝和鲍勃汇总了测量结果,并计算出了 AB、Ab、aB 和 ab 的平均值:

随后,他们将这些数值代入公式,发现(正的)结果竟然超过了 2!
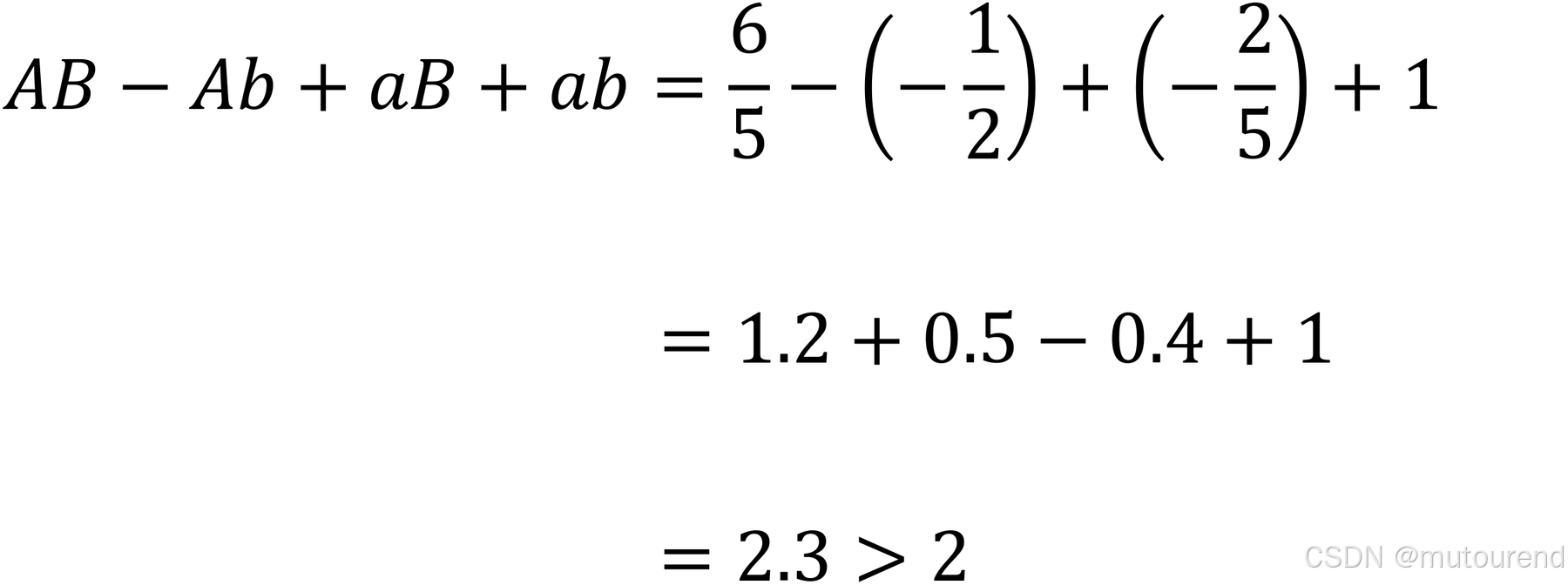
困惑之下,他们询问伯特尔曼教授这意味着什么。教授回答道:
- "人们常说,纠缠是量子力学的精髓。这个简单的数学不等式------即基于实验结果得到的公式在特定条件下其结果不可能大于 2------正是纠缠的核心所在。无论是经典相关性,还是隐藏变量理论所预测的相关性,都无法重现你们对我这双袜子所做的测量结果。由于你们得到的数值是 2.3,大于 2,唯一的解释就是:你们测量到的纠缠本质上是一种量子力学现象。因此,每一双袜子确实是真正发生了纠缠。在你们进行测量之前,并不存在所谓的左袜颜色或右袜颜色;它们是一个单一的量子对象。"
尽管现实世界中(至少目前)还没有真正让袜子发生纠缠,但已经有大量实验表明,量子相关性可以超越如上所述的 贝尔不等式。最早的实验实现了电子和光子的纠缠,而在随后的几十年里,科学家们甚至成功地让微小的纳米尺度物体发生纠缠,如一对亚微观的小型振动鼓。
那么,纠缠究竟是什么?在最初的定义中,曾说过:
- "纠缠是多个物体共享同一个量子态。"
结合本文所学到的内容,可以对这一定义加以更新:
- 纠缠是多个物体共享量子态的程度。
通过检验测量结果之间的相关性,可以量化不同物体之间存在多少纠缠。处于纠缠状态的物体,其状态无法被独立描述。伯特尔曼教授那双相距数光年的量子袜子,不能被简化为一只左袜的颜色和一只右袜的颜色;在被测量并解除纠缠之前,它们始终作为一个颜色不确定的整体存在。
在量子计算机中,量子比特之间相隔的是毫米级距离,而不是光年级距离。但这一原理依然成立:一对纠缠的量子比特确实是一个量子对象------至少在爱丽丝或鲍勃对其进行测量之前。
参考资料
1\] 2022年6月博客 [What Is Quantum Entanglement?](https://spectrum.ieee.org/what-is-quantum-entanglement) ## 附录:关于量子纠缠的历史插曲 人们对纠缠的焦虑,源自著名的 [1935 年 EPR 论文 Can Quantum-Mechanical Description of Physical Reality Be Considered Complete?](https://cds.cern.ch/record/405662/files/PhysRev.47.777.pdf),作者是 [阿尔伯特·爱因斯坦(Albert Einstein)](https://spectrum.ieee.org/tag/albert-einstein)、鲍里斯·波多尔斯基(Boris Podolsky)和内森·罗森(Nathan Rosen)(合称 EPR,取自他们姓名的首字母)。EPR 指出,量子力学描述了一个非确定性、非局域的世界,并据此认为这些特性表明量子力学作为一种理论是不完备的。[爱因斯坦](https://spectrum.ieee.org/tag/einstein) 尤其担忧缺乏局域性的问题。他曾将纠缠粒子之间瞬时的测量更新著名地称为"*spukhafte Fernwirkung*"("幽灵般的远距作用"),因为他无法将其与"物理学的思想体系"相协调。以下摘自爱因斯坦写给马克斯·玻恩(Max Born)的信件: * *"如果有人问......物理学思想世界的特征是什么,首先映入眼帘的是这样一点:物理学的概念指向一个真实的外部世界......这些物理对象的另一个特征在于,它们被安排在一个时空连续体中。物理学中这种事物排列方式的一个本质方面在于:在某一时刻,它们主张彼此独立地存在。"* 为了保留这些看似合理的假设,并将物理学从量子力学所引入的、似乎难以调和的怪异性中"拯救"出来,物理学家开始探索所谓的"隐藏变量理论(hidden-variable theories)"。 根据隐藏变量理论,在爱丽丝和鲍勃的实验中,这些量子袜子的颜色其实早已由某个"隐藏"的变量预先决定好了。爱丽丝对第一只袜子的测量之所以*看起来*像是瞬间更新了另一只袜子的颜色,只是一种表象。人们曾认为,隐藏变量理论可以在不牺牲局域实在性的前提下,重现量子力学所预测的所有古怪结果。 也正是在这里,回到了本文的核心主题------因为量子纠缠正处在关于隐藏变量理论争论的中心位置。 如果隐藏变量理论是正确的,那么纠缠只是一种非局域性的*幻觉*;在这种情况下,伯特尔曼教授的量子袜子实际上并不会在距离无关的情况下存在某种奇异联系。但如果隐藏变量理论是错误的,那么纠缠就确实会将这些袜子联系在一起,无论它们相距多远。 在尚无法通过实验区分这两种理论之前,物理学家们只能将这一难题归入哲学讨论的范畴------直到前文提到的那位北爱尔兰物理学家贝尔(Bell)找到了突破口。