频散曲线与面波成像

[Graphical Abstracts](#Graphical Abstracts)

[1. 采样体积（Sampling Volume）的物理本质](#1. 采样体积（Sampling Volume）的物理本质)

[2. 能量的"延迟"效应（散射与路径弯曲）](#2. 能量的“延迟”效应（散射与路径弯曲）)

[3. 统计平均下的等效模量](#3. 统计平均下的等效模量)

[4. 总结：地震学中的体现](#4. 总结：地震学中的体现)

频散曲线

[1. 核心物理机理：波长的"感知深度"](#1. 核心物理机理：波长的“感知深度”)

[2. 几何机理：边界条件与陷波 (Trapped Waves)](#2. 几何机理：边界条件与陷波 (Trapped Waves))

[3. 地震学背景下的两种速度](#3. 地震学背景下的两种速度)

[4. 为什么频散曲线对地震学家如此重要？](#4. 为什么频散曲线对地震学家如此重要？)

[5. 总结](#5. 总结)

频散曲线的提取

[1. 频率-波数法 (f-k Analysis) ------ 最经典的方法](#1. 频率-波数法 (f-k Analysis) —— 最经典的方法)

[2. 多重滤波技术 (Multiple Filter Technique, MFT) ------ 单台记录的神器](#2. 多重滤波技术 (Multiple Filter Technique, MFT) —— 单台记录的神器)

[3. 相移法 (Phase Shift Method) ------ 主动源探测首选](#3. 相移法 (Phase Shift Method) —— 主动源探测首选)

[4. 提取后的"最后一步"：拾取 (Picking)](#4. 提取后的“最后一步”：拾取 (Picking))

[5. 总结流程](#5. 总结流程)

Graphical Abstracts

Source: Yang, XH., Zhou, Y., Han, P. et al. Near-Surface Rayleigh Wave Dispersion Curve Inversion Algorithms: A Comprehensive Comparison. Surv Geophys 45, 773--818 (2024). https://doi.org/10.1007/s10712-024-09826-y

注意：

（1）频散曲线存在的根本原因是地球存在"边界面"和"内部结构非均匀"。这意味着，对于完全均匀或者无边界的情况，不存在频散。

（2）频散曲线表现为频率和速度的关系，但本质上，并不是不同频率的波在均匀介质中的传播速度的差异（同一介质，波速固定，与频率无关），而是不同频率的波在同一介质中，对空间非均匀结构做了不同尺度的平均。

对第（2）条进一步解释：为什么不同频率的波对空间非均匀结构的不同尺度的平均，表现为波速的差异

简单来说，当波穿过一个非均匀结构时，它"感知"到的并不是每一个细小的杂质，而是在它波长尺度内所有物质的综合性能。

以下是为什么"尺度平均"会表现为"波速差异"的三个核心原因：

1. 采样体积（Sampling Volume）的物理本质

地震波不是一根纤细的线，而是一个具有厚度的波带（Fresnel Zone）。

大尺度波（低频/长波）： 它的"视野"极广。它会同时扫过岩石中的裂隙、空隙和固体颗粒。它感知的速度是这些物质体积加权平均后的结果（类似于并行电路的综合电阻）。
小尺度波（高频/短波）： 它的"视野"很窄。它可能只从坚硬的岩石颗粒间穿过，或者被一个小裂隙挡住。它感知的是局部细节的速度。

结论： 不同的平均尺度（即波长）决定了波所"包含"的非均匀体比例，比例不同，等效出的物理性质（模量和密度）自然不同，从而导致波速差异。

2. 能量的"延迟"效应（散射与路径弯曲）

非均匀性不仅改变了平均密度，还改变了波行进的"效率"。

微观层面（散射）： 当波遇到尺度远小于波长的非均匀体时，能量会发生散射。虽然一部分能量继续前行，但多次散射会导致波阵面（Wavefront）的相干性受损，宏观上表现为波的传播变得"吃力"，速度看起来变慢了。
宏观层面（路径选择）： 即使在平均意义上，如果结构是非均匀的，波会自动选择最快路径（Fermat's Principle）。但在大尺度平均下，这些微小的"捷径"会被平滑掉，剩下一个较慢的平均速度。

3. 统计平均下的等效模量

波速 $V$ 的基本公式是：

其中 $M$ 是弹性模量， $\\rho$ 是密度。

当你对空间非均匀结构做不同尺度的平均时，你实际上是在重新定义 $M$ 和 $\\rho$ ：

Backus Average（层状平均）： 如果你在垂直于地层的方向做大尺度平均，原本由"硬-软-硬"组成的序列会被等效为一个单一的、较软的介质。这是因为在受压时，软层贡献了大部分位移（类似串联弹簧）。
Voigt/Reuss Bounds： 不同的空间排布方式（并行或串行）会导致平均后的等效模量完全不同。

这种统计学上的等效模量随空间尺度变化 的现象，在宏观上最直观的表达就是速度的变化。

4. 总结：地震学中的体现

这正是你之前问到的 频散（Dispersion） 的深层机理：

低频波 ：平均了深部大尺度的均匀结构表现为较快的平均速度。
高频波 ：平均了浅部小尺度的非均匀结构（如风化层、沉积层）表现为较慢的平均速度。

核心逻辑： 平均尺度等效物理参数（模量/密度）的变化观测速度的变化。

频散曲线

在地震学中，频散曲线（Dispersion Curves）的存在并不是偶然的，它是介质的不均匀性（特别是分层结构）与波的干涉理论共同作用的结果。

简单来说：如果地球内部是完全均匀的一块石头，频散就不会存在。 频散之所以存在，是因为地球是"分层"的。

1. 核心物理机理：波长的"感知深度"

这是理解地震波频散最直观的钥匙。地震面波（如 Rayleigh 波或 Love 波）的能量并不是只在表面传播，而是会向地下渗透一定的深度。这个渗透深度与波长成正比。

长波（低频）： 能量能够"照"到地球深处。深部的岩石通常压力大、密度高，波速极快。因此，长波跑得快。
短波（高频）： 能量只集中在浅表。浅层通常是松散的沉积物或风化层，波速很慢。因此，短波跑得慢。

结论： 因为不同频率的波"探测"到了不同深度的速度，所以它们表现出的**整体传播速度(平均速度)**就不同。

2. 几何机理：边界条件与陷波 (Trapped Waves)

从波的干涉角度看，面波本质上是在地表和地下不连续面（如莫霍面）之间来回反射、不断叠加而形成的驻波。

相长干涉： 只有当波的频率与地层的厚度、波速满足特定的相位匹配条件时，波才能持续传播而不相消。
本征模式： 对于每一个频率，为了保持这种"相长干涉"，波必须以一个特定的速度运行。
这种受几何边界（地层界面）约束而产生的速度变化，被称为几何频散。

3. 地震学背景下的两种速度

在频散曲线中，我们通常讨论两种速度，它们的分离正是频散存在的证明：

相速度 (Phase Velocity, $v_p$ )： 某一个特定频率的波峰（单一正弦波）移动的速度。
群速度 (Group Velocity, $v_g$ )： 由多种频率组成的"波包"（能量中心）移动的速度。

关系公式：

(其中 $k$ 是波数)。如果没有频散（ $dv_p/dk = 0$ ），那么相速度就等于群速度，波包在传播中形状保持不变。

4. 为什么频散曲线对地震学家如此重要？

频散曲线本质上是地下结构的一张"指纹图"。

反演 (Inversion)： 只要我们在地表记录到了面波，提取出它的频散曲线（即：哪个频率跑了多快），我们就可以通过数学模型反推回地下的结构。
层析成像： 如果频散曲线显示高频部分极慢，说明地表有很厚的软土层；如果低频部分突然变快，说明深部有坚硬的地幔物质。

5. 总结

频散曲线存在的机理可以总结为：

垂直不均匀性：地球是分层的，深浅速度不同。
深度敏感性：波长决定了波能"看到"多深。
干涉约束：边界条件强制不同频率必须以不同速度传播。

你想深入了解一下如何通过观测到的"地震波波形"把这条曲线提取出来吗？（例如使用频率-波数 $f-k$ 分析法）

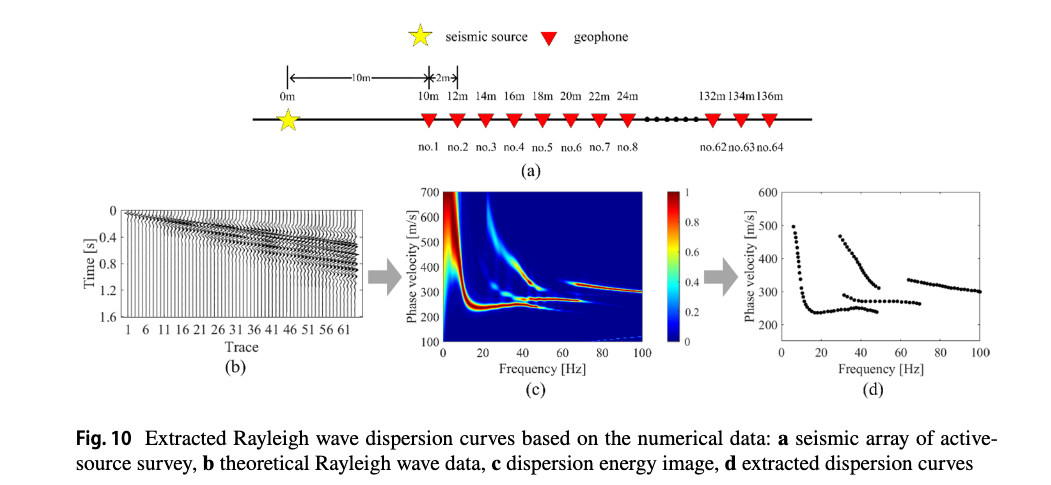
频散曲线的提取

提取频散曲线是地震学处理中的核心步骤，这个过程被称为**"色散分析"或"频散分析"**。其本质是：将混乱的时域信号（地震波形）转换到能直接看清速度与频率关系的"能量场"中。

以下是三种主流的提取方法，按其原理从简单到复杂排序：

1. 频率-波数法 (f-k Analysis) ------ 最经典的方法

这是最直观的方法，适用于台阵（Array）观测（即有一排地震计同时记录）。

原理：利用二维傅里叶变换，将时间 ( $t$ ) 转换成频率 ( $f$ )，将空间位置 ( $x$ ) 转换成波数 ( $k$ )。
提取过程：
1. 对所有台站的波形做二维变换。
2. 在得到的 $f-k$ 能量图中，能量最集中的地方会形成一条条脊线。
3. 利用公式 $v = f/k$ ，将能量点的坐标转换为速度。
特点：能分清信号的传播方向，抗噪声能力强。

2. 多重滤波技术 (Multiple Filter Technique, MFT) ------ 单台记录的神器

如果你只有一个地震台站，也可以提取频散曲线（主要是群速度）。

原理：利用一系列窄带滤波器，逐个提取不同频率的成分。
提取过程：
1. 设定一系列中心频率（比如 0.1Hz, 0.2Hz...）。
2. 用滤波器把这些频率成分单独"抠"出来。
3. 看每个频率的能量包（波包）什么时候到达。
4. 速度 = 距离 / 到达时间。
特点：非常适合处理远震面波，是研究地壳深部结构的常用手段。

3. 相移法 (Phase Shift Method) ------ 主动源探测首选

在城市浅层探测（如 MASW 方法）中最为常用。

原理：假设面波是以平面波形式传播，通过补偿不同台站之间的相位差来寻找能量最强的速度。
提取过程：
1. 给定一个尝试速度 $v$ 。
2. 计算该速度下各个台站理论上的相位延迟，并将其"对齐"。
3. 如果对齐后能量叠加最强，说明这个尝试速度就是该频率下的真实相速度。
4. 遍历所有频率，扫出一张能量图（称为"频散能量图"）。

4. 提取后的"最后一步"：拾取 (Picking)

当你得到上述方法的"能量图"后，你会看到明亮的条带：

手动或自动拾取 ：在能量最高的脊线上点选一系列点，这些点连接起来就是该场地的实测频散曲线。
基阶与高阶：能量最强的一条通常是"基阶（Fundamental mode）"，上方较弱的条带是"高阶（Higher modes）"。

5. 总结流程

地震记录 (波形图) $\\rightarrow$ 数学变换 (f-k/MFT/相移) $\\rightarrow$ 能量分布图 $\\rightarrow$ 脊线拾取 $\\rightarrow$ 频散曲线

提取出这条曲线后，下一步就是**"反演"**------通过这条曲线猜出地下到底有几层土、几层岩石，以及它们的剪切波速度 ( $V_s$ ) 是多少。