CNN神经网络正向/反向推导

一、 神经网络的"原子"操作

神经网络是由层层叠加的运算组成的，理解了其中一层的传递，就理解了整个网络。

二、 符号定义：统一我们的"语言"

在推导之前，我们需要规范一下符号（这也是阅读论文的基础）：

• 上标 L：表示第 L 层。

• ：表示第 L 层的神经元数量。

• ：第 L-1 层的激活输出（Activation），即第 L 层的输入。

三、 正向推导：Z 与 A 的二重奏

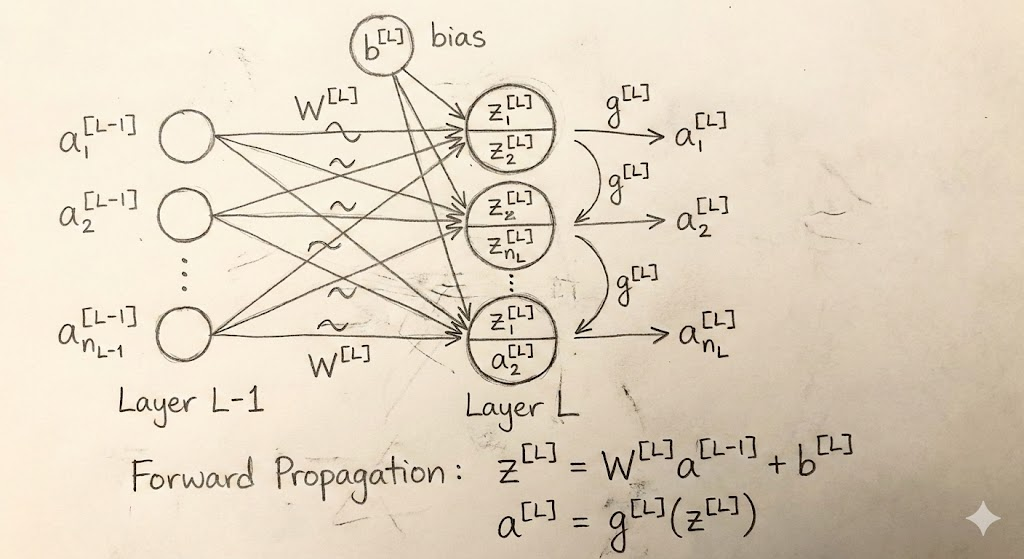
从第 L-1 层传递到第 L 层，本质上可以分解为两个数学步骤：

1. 线性求和 (The Linear Step)

首先，我们需要对上一层的输入进行加权求和并加上偏置。这是信息的"汇聚"过程。

公式如下：

• (权重矩阵)： 决定了连接的强度。

• (偏置向量)： 类似于线性方程 中的截距，调整激活的阈值。

• (中间变量)： 此时的结果还是线性的。

2. 非线性激活 (The Activation Step)

如果网络只有线性部分，无论叠加多少层，它本质上还是一个线性模型。为了学习复杂的特征，我们需要引入激活函数。

公式如下：

• 可以是 Sigmoid, Tanh 或 ReLU 等函数。

• 就是这一层最终输出给下一层的信号。

3. 矩阵维度的那些坑 (Dimension Check)

在 Python (NumPy/PyTorch) 实现时，最头疼的就是 Shape Mismatch。让我们来核对一下维度：

• ，行数等于当前层的神经元数，列数等于上一层的神经元数

• （此处 m 为样本数量，如果是单样本则为 1）

• 

• 和 :

四、反向推导

正向传播算出了预测值，发现和真实值有误差（Loss）。反向传播就是要把这个"锅"（误差）甩回去，告诉前面的每一层："你们的参数（W和b）该怎么改！"

我们的目标是最小化损失函数 J。我们需要知道每一个权重 W 和偏置 b 对最终损失 J 的"贡献"有多大，以便根据梯度下降法更新它们。

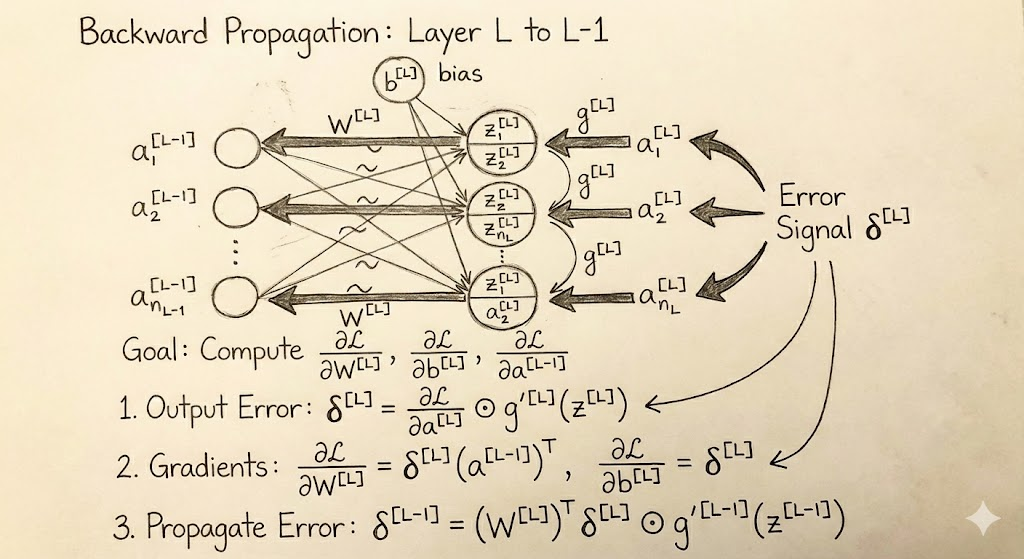
核心工具：链式法则 (The Chain Rule)

反向传播的本质，就是从后往前，一层层剥洋葱。

假设我们要计算损失 J 对第 L 层变量 z 的导数，我们需要先知道 J 对 a 的导数：

为了方便工程实现，我们用 来表示 。

1. 计算当前层的中间梯度

这是反向传播的起点（对于当前层而言）。

• ：后一层传回来的梯度（如果是最后一层，则是损失函数的导数）。

• ：当前层激活函数的导数（如 Sigmoid 的导数是 a(1-a)，ReLU 的导数是 1 或 0）。

• 注意：这里是 Element-wise product（对应元素相乘）。

2. 计算当前层参数的梯度 ()，这一步是为了更新参数。

• 工程视角： 为什么要转置 ？

  • 维度:

  • 维度:

  • 为了得到 的 dW，必须让转置，变成 ，这样矩阵乘法才成立。

3. 计算传给上一层的梯度 (关键连接)

这是这一层对上一层的"反馈"，也是反向传播能继续下去的关键。

• 这里我们再次使用了矩阵转置。 的转置将梯度从 维空间映射回 维空间，从而完成误差的回传。